高速液体クロマトグラフィー(HPLC)のデータ分析プログラムをPythonで作成しました。
追記1:導関数を明示的に与えることで高速化されました。
追記2:部分フィットの後に全体フィットすることで正確性アップしました。
追記3:ベースライン推定を本格的にしました。
コードは以下にあります。
https://github.com/yoshiF7d/lc
分析のステップ
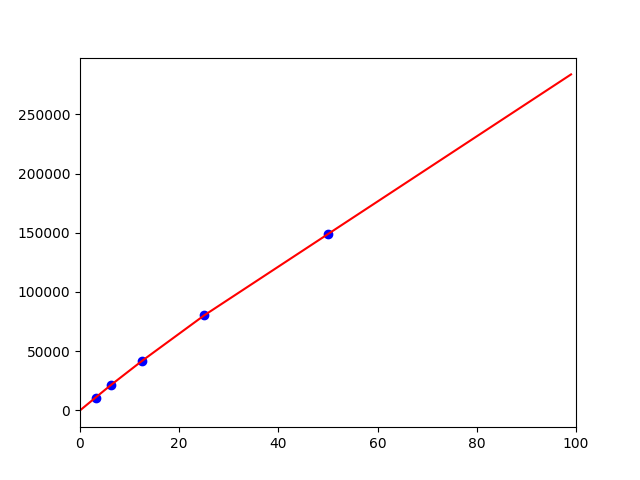
検量線を作成する
まず含まれている物質の濃度がわかっている標準サンプルを、濃度を変えていくつか作りデータをとります。このデータから、「物質Aが濃度Cのときこんなデータになる」というのがわかります。以下の表は標準サンプルにどの物質がどの濃度で含まれているかを示します。
| STD1.txt | STD2.txt | STD3.txt | STD4.txt | STD5.txt | |
|---|---|---|---|---|---|
| Maleic Acid | 50 | 25 | 12.5 | 6.25 | 3.125 |
| Glucose | 100 | 50 | 25 | 12.5 | 6.25 |
| Xylose | 50 | 25 | 12.5 | 6.25 | 3.125 |
| Glycerol | 50 | 25 | 12.5 | 6.25 | 3.125 |
| Acetic Acid | 50 | 25 | 12.5 | 6.25 | 3.125 |
| Ethanol | 30 | 15 | 7.5 | 3.75 | 1.875 |
| n-Buthanol | 30 | 15 | 7.5 | 3.75 | 1.875 |
この5つのサンプルをHPLCにかけた結果が以下のようになります。
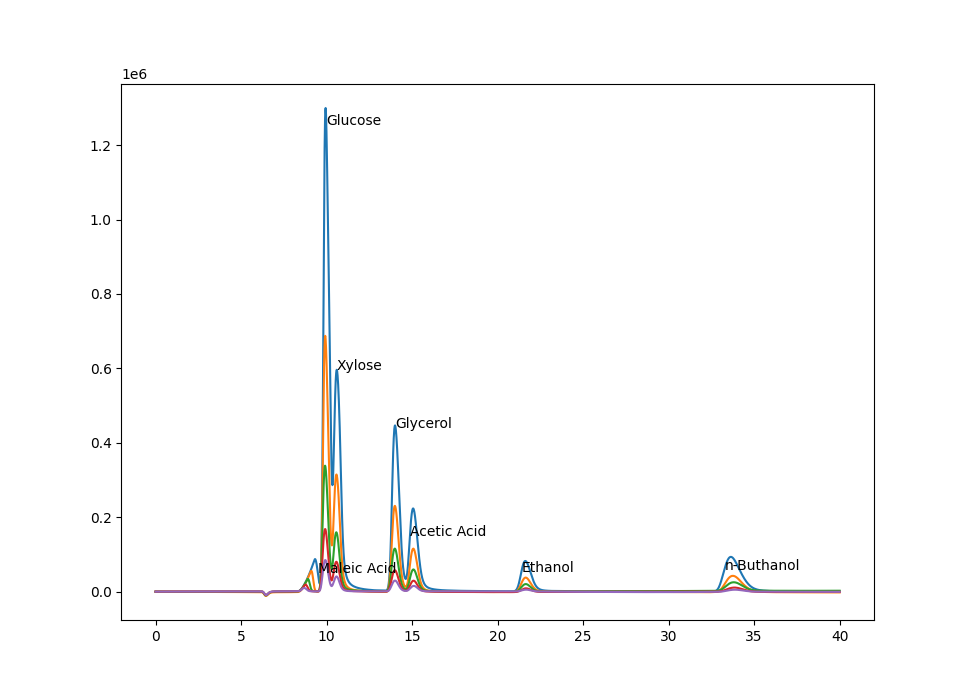
色の違いがサンプルの違いです。異なるピークは異なる物質を表します。
未知サンプルを分析する
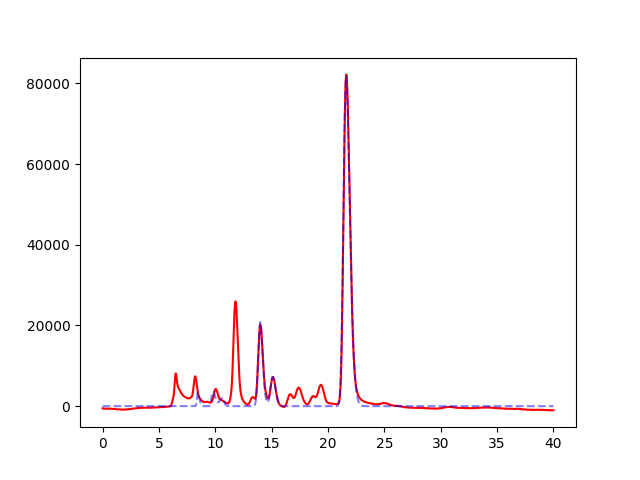
標準サンプルのデータと未知サンプルのデータを比較して、未知サンプルに含まれている既知の物質の濃度を推定します。赤線は未知サンプルのデータで、青点線は、既知サンプルのデータをもとにしたフィッティング曲線です。例えば以下の未知サンプルにはEthanolが多く含まれているということがわかります。
プログラムの流れ
標準サンプルデータからフィッティングパラメータを作成する
標準サンプルのまとめファイルと標準サンプルのデータを読み取る
STDTというクラスに標準サンプルに関するすべてのデータをまとめます。
self.tableに標準サンプルのまとめファイル、self.dataに標準サンプルのデータをいれます。
with open(stdfile) as f:
reader = csv.reader(f)
self.table = [row for row in reader]
for file in list(map(lambda s:os.path.join(self.dir,s),self.table[0][1:])):
if file.endswith('.txt'):
self.data.append(LCData(file).query(HEADER))
まとめファイルにある化合物の数だけピークを読み取る
scipy.find_peaksモジュールを使い、ピークを検出します。ピークが十分な高さをもつという指標として、yデータの標準偏差を使っています。
stdev=np.std(y)
peaks,props = find_peaks(y,prominence=0.1*stdev,width=15)
リストdataから大きい順番にcountとる関数pickを使ってピークの大きいものからまとめファイルにある化合物の数だけ選びます。このリストをまたxの小さいほうから順番に並び替えます。
def pick(data,count):
return np.argsort(data)[::-1][:count]
ind = pick(y[peaks],len(self.table)-1)
ind2 = pick(peaks[ind],len(ind))[::-1]
ピークの位置とピークの幅は、後でフィッティングの初期値に使うので保存します。
peaks = peaks[ind][ind2]
width = props["right_ips"][ind][ind2] - props["left_ips"][ind][ind2]
非対称ガウス関数でフィッティングする
Skew normal distribution という非対称なガウス関数を使ってフィッティングします。
この関数は以下のような形で、$x_0$はピークの位置、phはピークの高さを決め、wはピークの幅、skはピークの歪みを決めます。
f(x) = \textrm{ph}\cdot\left(1+\textrm{erf}\left(\textrm{sk}\cdot\frac{x-x_0}{w}\right)\right)\cdot e^{-(x-x_0)^2/w^2}
モデル関数は以下のように定義します。
def asymGaussModel(x,x0,ph,w,sk):
e = (x-x0)/w
return ph*(1 + erf(sk*e))*np.exp(-e*e)
scipy.optimize.least_squaresを使ってフィッティングします。least_squaresは誤差関数を受け取って、それを最小にするパラメータを探してくれます。このままフィッティングをすると、モデル関数のピークの位置が好き勝手に動いてしまい、狙ったピークにフィットさせることができません。そこで以下のような工夫をしました。
まずそれぞれのピークの範囲を求めます。これはboundという関数で行っています。この関数はピークの位置の左右を探索し、下降から上昇に転じた点をそのピークの範囲として返します。ノイズに強くするため5つの点の移動平均をとっています。
次にその範囲だけ1になるような重みデータを作って、誤差関数はその重みを受け取って、重みをかけた値を返すようにします。こうすることで、フィッティング時に望みピークの範囲以外は無視されます。
bd = bound(y,p)
for k in range(len(x)):
if k < bd[0] or k > bd[1]:
w[k] = 0
else:
w[k] = 1
重み関数の導入で、実質的には以下のように分割されたピークに対してフィッティングがかかるようになりました。カクカクが生じていますが重みがゼロのところは誤差関数もゼロになるので問題ありません。
誤差関数は以下のようになります。pはパラメータの配列、xはxデータ(といってもrange(len(y))),yはyデータ、wが重みデータです。
def errorAGM(p,x,y,w):
return w*(asymGaussModel(x,*p) - y)
p0 はパラメータの初期値を入れます。初期値にはfind_peaksで求めたピークの位置、高さ、ピーク幅を使い、歪みはゼロとします。'least_squares'によりフィッティングを行います。
p0 = [peaks[i],y[peaks[i]],width[i],0]
pout = (least_squares(errorAGM,x0=p0,args=(xi,y,w))).x
任意の濃度に対するパラメータを返す補完関数を作る
前のステップで、標準サンプルから、特定の濃度に対するパラメータの対応表が作られます。これが前に述べたParams.csvに保存される内容になります。
Maleic Acid,x0,ph,w,sk
50.0,1139.8046919960632,47207.218519487535,74.49852363132098,-4.549015741018971
25.0,1106.7983818867626,30422.59219838259,54.01453972009471,-4.6763456289474545
12.5,1082.7336843125813,20222.5458987428,43.456448177695584,-3.0325457757929897
6.25,1064.940231744898,13315.21731560561,33.96700110133946,-1.5821469563423958
3.125,1030.3607800967384,7745.22985904961,32.05016009058917,1.1070130304633512
この対応表から、任意の濃度cのときのパラメータを求めるため、interpolate.interp1dを用いて
補完関数を作ります。濃度0のときはピークの高さは0いう"常識"のデータ点を一個増やして補完しています。
if j == 2:
x.append(0)
y.append(0)
fit = interpolate.interp1d(x,y,kind='linear',fill_value='extrapolate')
この補完関数を使って、ある濃度のときのパラメータを返す関数intpを作っておきます。
パラメータを用いて未知サンプルデータをフィッティングする
フィッティングの初期値として使う濃度を推定する
パラメータリストから化合物の大体のピークの位置がわかるので、その位置の高さからだいたいの濃度を推定します。データが負のときは濃度0とします。
x0 = np.average([p[j][1] for j in range(1,len(p))])
c = (data[np.floor(x0).astype(int),1] / p[1][2]) * p[1][0]
if c > 0:
concs[i] = c
else:
concs[i] = 0
フィッティングを行う
誤差関数を以下のように定義します。concsは各化合物の濃度の配列です。それぞれの濃度に対するパラメータをintpで取得し、そのパラメータの曲線をasymGaussModelで取得して、それらの合計をyデータから引きます。
def error(self,concs,x,y):
err = 0
for i,c in enumerate(concs):
p = self.intp(i,c)
err += asymGaussModel(x,*p)
return y - err
フィッティングを行います。
cout = (least_squares(self.error,x0=concs,bounds=(0,np.inf),args=(x,y))).x
アップデート
導関数を明示的に与える
least_squareルーチンはjacという変数に誤差関数の導関数を与えることで高速かつ正確になります。歪ガウス関数のパラメータの変化に対する導関数は数学的に求まるので、これを関数にします。least_squareのマニュアルではヤコビアンといってますが、これは単に各パラメータについての導関数のリスト(勾配)のデータ長分のリストです。ようはxが違ったら勾配も違うので、xの数だけ勾配を並べます。numpyの配列を引数として与えれば勝手に戻り値の配列を考えてくれるので、単に勾配を返す関数を書いてください。ただし転置してください。
def wjacAGM(p,x,y,w):
return np.transpose(w*np.transpose(jacAGM(p,x,y)))
def jacAGM(p,x,y):
e = (x-p[0])/p[2]
f = 1+erf(e*p[3])
g = np.exp(-e*e*p[3]*p[3])/np.sqrt(np.pi)
h = p[1]*(-p[3]*g + e*f)/p[2]
j0 = 2*h
j1 = f
j2 = 2*e*h
j3 = 2*e*g*p[1]
return np.transpose([j0,j1,j2,j3]*np.exp(-e*e))
pout = (least_squares(errorAGM,x0=p0,jac=wjacAGM,args=(xi,y,w))).x
また、メインのフィッティングにもこの導関数の情報を活かせます。メインのフィッティングでは、パラメータの変化に対する導関数ではなく、濃度の変化に対する導関数が必要です。濃度は線形補間の関数intpから求まります。intpの導関数の2点を適当にとって傾きを求め、以下のような微分のチェーンルールから導関数を求めます。
\frac{\partial}{\partial c} =
\frac{\partial}{\partial p_1} \frac{\partial p_1}{\partial c} +
\frac{\partial}{\partial p_2} \frac{\partial p_2}{\partial c} +
\frac{\partial}{\partial p_3} \frac{\partial p_3}{\partial c} +
\frac{\partial}{\partial p_4} \frac{\partial p_4}{\partial c}
def jac(self,concs,x,y):
dc = 0.01
res=[]
for i,c in enumerate(concs):
p = self.intp(i,c)
dpdc = (self.intp(i,c + 0.5*dc) - self.intp(i,c - 0.5*dc))/dc
res.append(np.dot(jacAGM(p,x,y),dpdc))
return - np.transpose(res)
jacAGM(p,x,y)が歪みガウス関数のパラメータ変化についての勾配でdpdcがパラメータ配列の濃度に関する微分です。これの内積が誤差関数の濃度変化についての勾配になります。jacAGM(p,x,y)は実際にはベクトルではなく上にのべたヤコビアンとかいう行列ですが、ドット積というのはうまく定義されてるので、勾配をベクトルと考えた場合とコードの形が変わりません。
cout = (least_squares(self.error,x0=concs,jac=self.jac,bounds=(0,np.inf),args=(x,y))).x
これでフィッティングが高性能化されました。
部分フィットから全体フィット
パラメータを求めるフィッティングのときに、ピークをまず分割して、分割したピークに対するフィッティングをかけていますが、この方法だとピークが重なる部分を過大評価してしまいます。このため、部分フィットの結果を初期値として全体フィットをかけるようにしました。全体フィットではすべてのモデル関数を一度に動かします。このため、least_squareにかける誤差関数のパラメータは4ではなく、$4 \times $ (ピーク数)になります。誤差関数の中でパラメータを4つずつに分解し、それに対応する歪ガウス関数の効果を足し合わせます。
def errorWhole(self,p,x,y):
n = len(self.params)
err = 0
for i in range(n):
pp = p[4*i:4*(i+1)]
err += asymGaussModel(x,*pp)
return y - err
def jacEW(self,p,x,y):
n = len(self.params)
j =[]
for i in range(n):
pp = p[4*i:4*(i+1)]
j.append(jacAGM(pp,x,y))
return -np.hstack(j)
導関数も求まるのでちゃんと定義します。部分フィットの結果poutを初期値として全体フィットpoutallを求めています。
pall = []
for i,p in enumerate(peaks):
bd = bound(y,p)
for k in range(len(x)):
if k < bd[0] or k > bd[1]:
w[k] = 0
else:
w[k] = 1
p0 = [peaks[i],y[peaks[i]],width[i],0]
pout = (least_squares(errorAGM,x0=p0,jac=wjacAGM,args=(xi,y,w))).x
for p in pout:
pall.append(p)
#self.params[i].append([float(self.table[1:][i][j+1]),pout[0],pout[1],pout[2],pout[3]])
pallout = (least_squares(self.errorWhole,jac=self.jacEW,x0=pall,args=(xi,y))).x
for i,p in enumerate(peaks):
pout = pallout[i*4:(i+1)*4]
self.params[i].append([float(self.table[1:][i][j+1]),pout[0],pout[1],pout[2],pout[3]])
以下のように過大評価をなくすことに成功しました。
部分フィットのみ

部分フィット+全体フィット

惑星の運動も、まず地球と太陽のみ、地球と火星のみなどの運動を解いてから、その結果をもとに、全ての惑星が同時に影響しあう解を求めるらしいですがそれと似ています。
ベースライン推定
基本は上のリンクの方法でベースラインの推定を行いました。ただし、この方法はピークのある部分をゼロから自動で推定する方式ですが、HPLCのデータの場合、ピークのある部分を別の方法で推定できそうだったので、それを初期推定として、そのあとは上の方式で重みを更新する方式にしました。
ピークのない部分を推定する
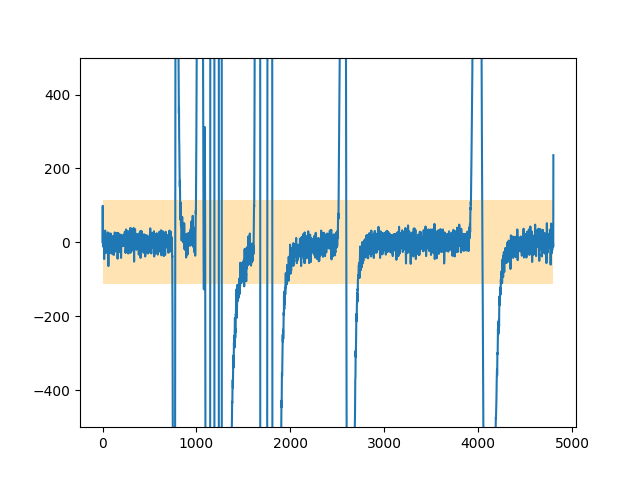
HPLCデータの一次微分をみると、以下のようにピークのない部分はゼロの近くで振動しているという特徴がありました。これを利用することにしました。
dif = np.diff(data,append=0)
std = np.std(dif)
hist,x = np.histogram(dif,bins=100,range=(-std,std),density=True)
まずヒストグラムをとります。するとガウス型になるので、このだいたいの幅を見積もります。なるべくマジックナンバーに頼らないために、標準偏差とか使ってます。
ガウス関数の積分=全面積という計算から幅を見積もりました。
\int_{-\infty}^{\infty} e^{-x^2/\sigma^2} dx = \sigma \sqrt{\pi}
np.histogramのdensity=Trueとすると全面積1になります。
s = 1.0/(np.max(hist)*np.sqrt(np.pi))
以下の図で青はヒストグラムです。オレンジは見積もったガウス関数です。
この幅の中にゼロ付近の振動が含まれます。先ほどの計算はこの幅を求めるためだけのものです。
この幅の中にデータ点がたくさんある部分を、"ベースラインがあるところ"と考えます。
まずガウス関数でこの範囲の内部だけに重みをもたせ、幅20のガウス関数で移動平均をとりました。
w = np.exp(-dif*dif/(s*s))
z = np.array(range(101))
z = np.exp(-(z-50)*(z-50)/(20*20))
w = np.convolve(w,z,mode='same')
結果以下のような重み関数ができました。
この重み関数を初期値として、上のリンクにある方式で重み関数を更新し、ベースライン推定を行いました。
ここでD = 1e+7*D.dot(D.transpose())の1e+7はマジックナンバーでベースラインの滑らかさを表します。ここをどう決めるべきかはまだわかってませんがこの数字でうまくいきました。また、ループを回す回数もマジックナンバーです。このループは重み関数の更新回数を表しますが、あまり回しすぎると変なベースラインになったので、10でとめるという適当なことしてます。ここらへんは改善の余地ありです。
def baseline(data):
w = calcw(data)
return calcz(data,w)
def calcw(data):
dif = np.diff(data,append=0)
std = np.std(dif)
hist,x = np.histogram(dif,bins=100,range=(-std,std),density=True)
s = 1.0/(np.max(hist)*np.sqrt(np.pi))
w = np.exp(-dif*dif/(s*s))
z = np.array(range(101))
z = np.exp(-(z-50)*(z-50)/(5*5))
w = np.convolve(w,z,mode='same')
x = np.convolve(x,[0.5,0.5],mode='valid')
return w/w.max()
def calcz(data,w):
y = data
l = len(y)
D = sparse.diags([1,-2,1],[0,-1,-2], shape=(l,l-2))
D = 1e+7*D.dot(D.transpose())
W = sparse.spdiags(w,0,l,l)
for i in range(10):
W.setdiag(w)
Z = W + D
z = spsolve(Z, w*y)
d = y-z
dn = d[d<0]
m = np.mean(dn)
s = np.std(dn)
wnew = w*expit(2 * ((2*s - m)-d)/s)
w = wnew
return z
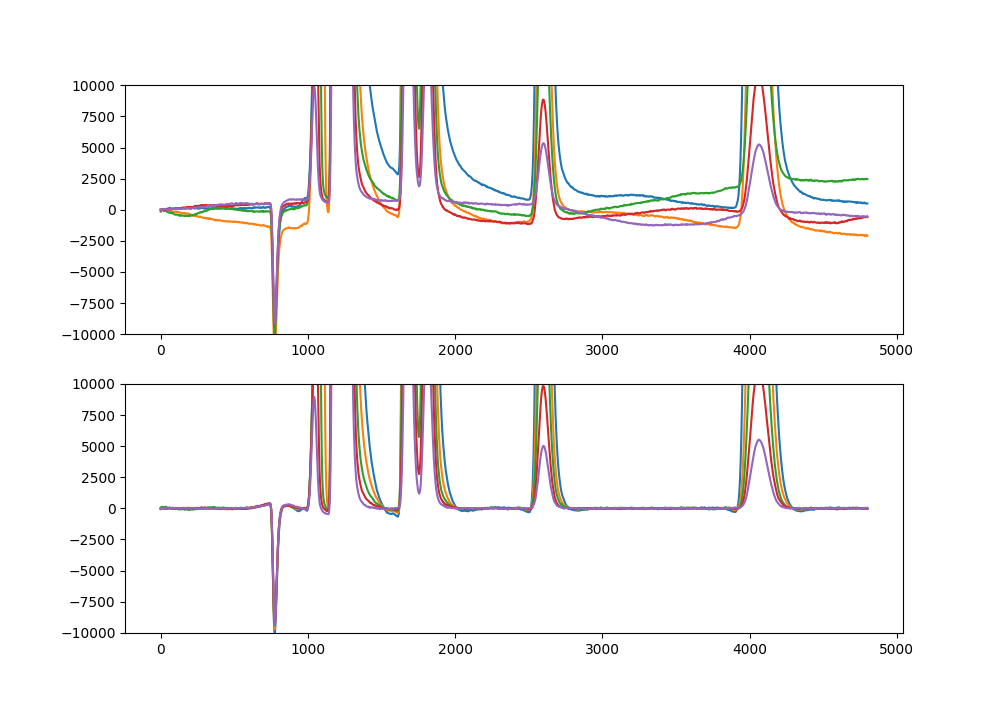
ベースライン修正の結果。上:修正前、下:修正後