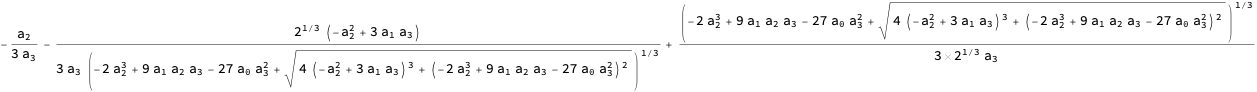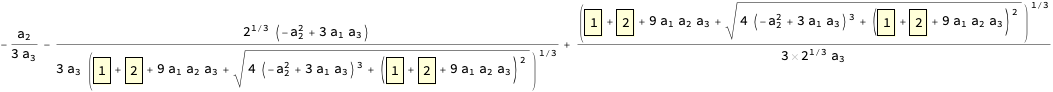辞書式圧縮による数式の簡略化 (Mathematica)

数式の簡略化

Mathematicaでは記号計算の結果、大変複雑な記号式が生成される場合があります。
Simplify,FullSimplifyは数式を変形して簡単にしてくれますが、
これらは、数式の中から繰り返しでてくる部分を見つけ、それを変数で置き換えるということはやってくれません。
今回はそれをやってくれる関数を作ります。

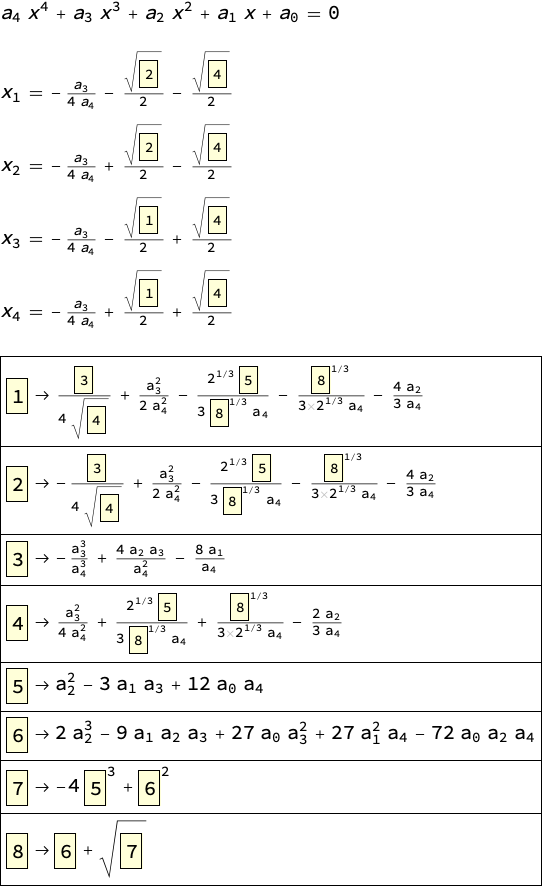
例えば、四次方程式 $0 = a_4 x^4 + a_3 x^3 + a_2 x^2 + a_1 x^1 + a_0$ の解はたいへん煩雑なものになります。

poly = Sum[Subscript[a, k] x^k, {k, 0, 4}];
sol = Solve[poly == 0, x];
MapIndexed[
  Style[TraditionalForm[Subscript[x, First[#2]] == #1], 20] &, 
  sol[[All, 1, 2]]] // Column

閲覧注意：四次方程式の解の公式

これをこれから紹介する関数DictionaryCompressを使うと次のように簡単化されます。

poly = Sum[Subscript[c, k] x^k, {k, 0, 4}];
sol = Solve[poly == 0, x];
expr = x /. sol;
Column[{Column[
     MapIndexed[
      Style[TraditionalForm[Subscript[x, First[#2]] == #], 20] &, #[[
       1]]], Spacings -> 1],
    Column[Style[#, 20] & /@ #[[2]], Spacings -> 1, Frame -> All]
    }] &@DictionaryCompress[expr, 1, 1, 
  Framed[#, Background -> LightYellow] &]

DictionaryCompressはこのようなコードです。

DictionaryCompress[expr_, count_, size_, func_] := Module[
  {t, s, rule, updateRule},
  updateRule[ruleloc_] := Module[{rule1, rule2, rulertn},
    rulertn = (# //. Cases[ruleloc, Except[#]]) & /@ ruleloc;
    rule1 = 
     Select[rulertn, ((! FreeQ[#, Plus]) && (! NumericQ[#[[1]]])) &];
    rule2 = Complement[rulertn, rule1];
    rulertn = rule1 //. (Reverse /@ rule2);
    rulertn = 
     rulertn /. MapIndexed[ Last[#1] -> func @@ #2 &, rulertn];
    rulertn
    ];
  t = Tally@Level[expr, Depth[expr]];
  s = Sort[
    Select[{First@#, Last@#, Depth[First@#]} & /@ 
      t, (#[[2]] > count && #[[3]] > size) &], #1[[2]]*#1[[3]] < #2[[
        2]]*#2[[2]] &];
  rule = MapIndexed[First[#1] -> func @@ #2 &, s];
  rule = FixedPoint[updateRule, rule, 3];
  {
   expr //. rule, Reverse /@ rule
   }
  ]

基本的なコード内容

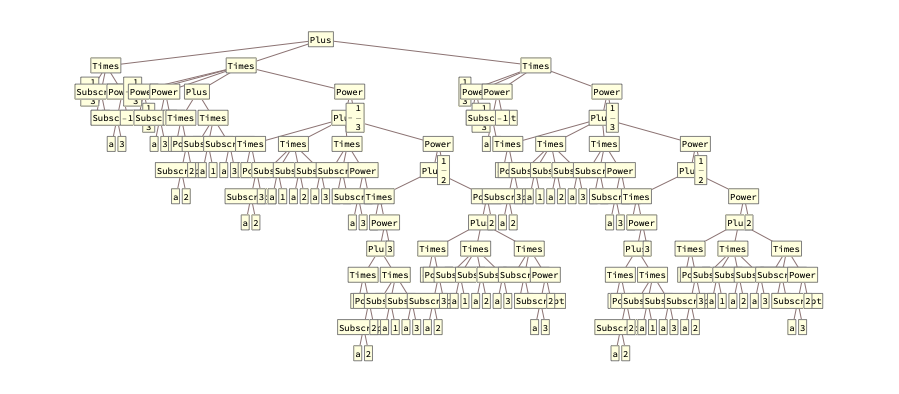
数式はツリー構造で表されます。例えば三次方程式の解は

poly = Sum[Subscript[a, k] x^k, {k, 0, 3}];
sol = Solve[poly == 0, x];
sol[[All, 1, 2]][[1]]

このような式ですが、これをツリー構造で表すと、

sol[[All, 1, 2]][[1]]//TreeForm

こうなります。

Levelはこのようなツリー構造のサブツリーを取得し、リストとして返します。またTallyはリストを調べ、例えばaがn個あったらそれらをまとめて{a,n}という形にしてくれます。これらを組み合わせると、式に含まれる部分式の一覧表を作ることができます。

expr=sol[[All, 1, 2]][[1]]]];
t=Tally[Level[expr,Depth@expr);
Column[#, Alignment -> Center, Dividers -> All] & /@ 
(
 {
  Style["Count : " <> ToString@Last[#], 20],
  Style["Size : " <> ToString@Depth[First[#]], 20],
  TreeForm@First[#]
 }& /@ t
) // Multicolumn

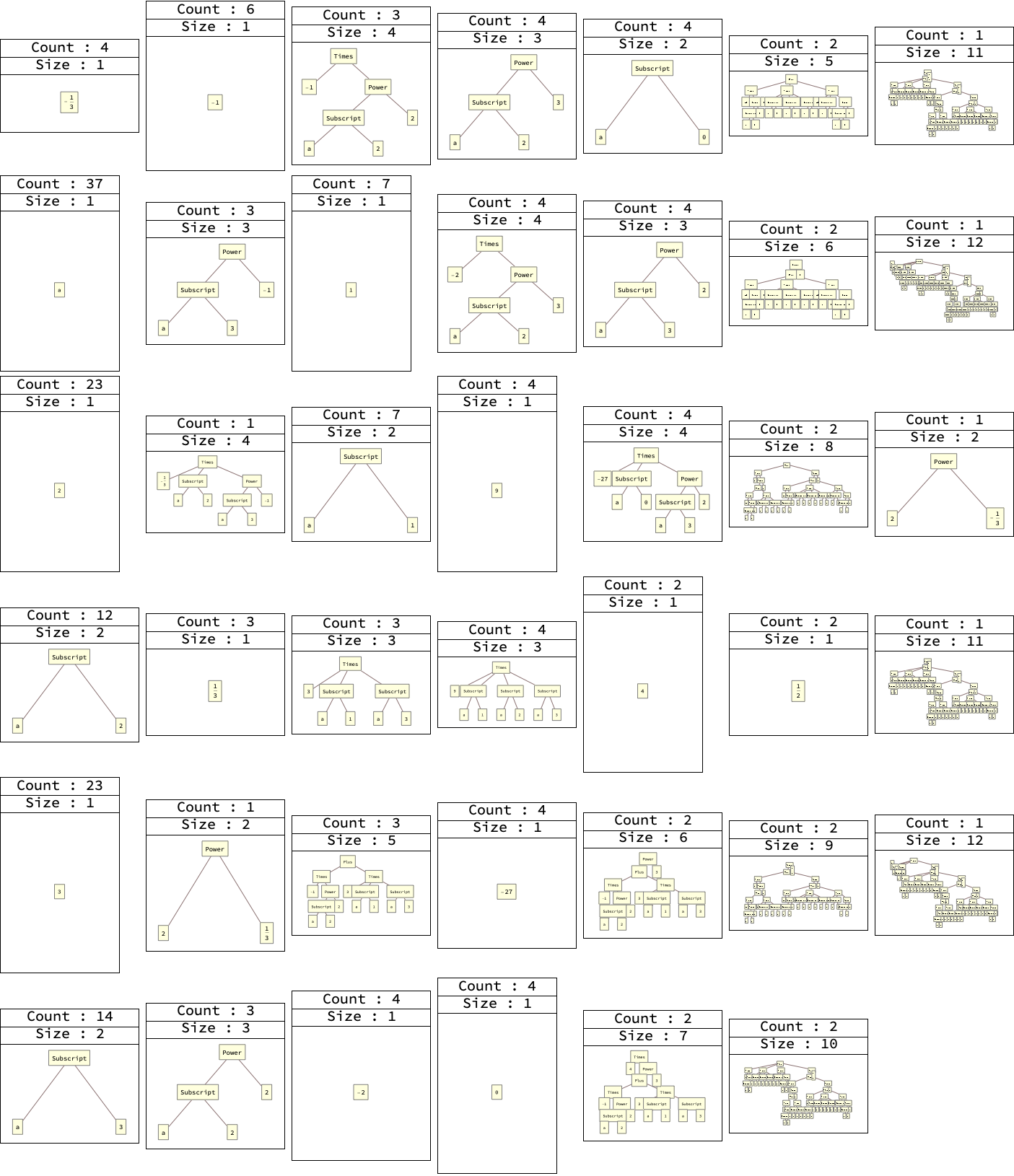
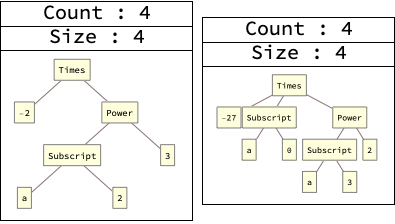
Countはもとの式にそのサブツリーが何回出現したか、Sizeはサブツリーの深さを表します。

一覧表ができたら、この中から、置き換えをする価値のある部分式を選びだします。出現頻度が高くサイズが大きいものがいいでしょう。CountとSizeに条件をつけて、その条件にあう部分式をSelectで選びだします。

s=Select[t,(Last[#]>3&&Depth[First[#]]>3)&];
Column[#, Alignment -> Center, Dividers -> All] & /@ 
(
 {
  Style["Count : " <> ToString@Last[#], 20],
  Style["Size : " <> ToString@Depth[First[#]], 20],
  TreeForm@First[#]
 }& /@ s
) // Multicolumn

これから部分式置き換えのルールを作成します。

rule=MapIndexed[First[#1] -> Framed[First@#2, Background -> LightYellow] &,s]

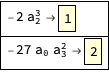
ReplaceRepatedでできたルールをもとの式に適用します。ReplaceRepatedはRuleをある式に対し、その式が変化しなくなるまで適用するというものです。
ReplaceRepatedはシンタックスシュガー//.があり、これを使って簡単にかけます。
ちなみに、Mathemataicaでは+や-もPlusやSubtractのシンタクッスシュガーです。Mathematicaで見慣れない記号があったらそれはなにかのシンボルのシンタクッスシュガーです。

expr //. rule

部分式置き換えができました！

プラスアルファ

上のコードだと、まだ少し能力が弱いものになります。
そこでDictionaryCompressでは、updateRuleという関数でルールを更新する仕組みをつけてあります。まず部分式置き換えのルールをたくさん生成したら、生成されたルールをお互いに作用させあいます。そうするといくつかはよりコンパクトな新しい置き換えルールになるので、これを繰り返してルールを更新していくという仕組みをつけています。

また、サイズや出現頻度という構造的な条件とは別に、数学的な条件で置き換えにふさわしい部分式を選ぶこともしています。
この条件は「足し算を最低一個含み、数字ではない」という条件です。
詳しくはコード読んでください！ありがとうございました！