Mathematicaで使われているWolfram言語のプログラミング言語としての特徴を紹介します。
Lisp型の言語
WLはLisp型の言語なので、あらゆる式がリストとして表現されます。一般的にすべての式は、
A[B1[C1[...], C2[...], ...], B2[...], B3[...], ...]という形をしています。
違いはLispで (func,a,b)と書くところを、func[a,b]と書くだけです。
+や*などの演算子は、シンタックスシュガーとして用意されていて、パースされると基本形式に変わります。例えば、a+(b+c)はPlus[a,Plus[b,c]]という式とみなされます。
4つのカッコ [],{},(),[[]]
WL言語では4つのカッコを使います。
関数、データ構造のカッコ[]
例えばfという関数をaに作用させたものは、f[a]という式になります。
WLが関数のカッコに()を使わないのは、a(b+c)のような式をaかけるb+cと読むためです。WLはもともと数式処理言語なので数式を自然に表現できるようになっています。
またf[a]はfというデータ型がaという要素を持っているという捉え方もできます。
このようにデータも関数もどちらも同じ形式で扱われます。なのでまとめてシンボルと呼ばれます。WLの定義ずみシンボルのリストはこちらで見れます。Mathematica 覚書
リストのカッコ{}
{a,b,c}はa,b,cを要素としてもつリストを表します。{a,b,c}の基本形式はList[a,b,c]となります。ここでListは関数ではなくデータ構造の名前としての役割をもっています。
普通のカッコ()
これは普通に式をまとめるためのカッコです。
配列のカッコ[[]]
aというリストのk番目の要素はa[[k]]となります。WL言語では配列の添字は1から始まります。
a[[-k]]はaの最後からk番目の要素を表します。多次元配列の場合、a[[i,All]]とすると、a[[i]]の要素すべてという意味になります。
あらゆる式が同じ基本構造をもつ
どんな複雑な式も同じ基本形式なので、恐れる必要がありません。式は、データもプログラムも表すので、式を操作する関数で、プログラムの操作や、プログラムの構造の表示などができます。
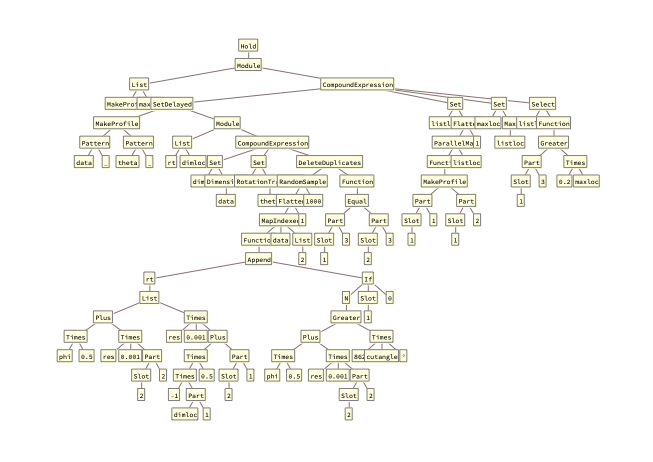
例えば以下のような複雑なプログラムは
Module[
{MakeProfile, maxloc},
MakeProfile[data_, theta_] := Module[
{rt, dimloc},
dimloc = Dimensions[data];
rt = RotationTransform[theta];
DeleteDuplicates[
RandomSample[
Flatten[
MapIndexed[
Append[
rt[{phi*0.5 + res*0.001*#2[[2]],
res*0.001*(-dimloc[[1]]*0.5 + #2[[1]])}],
If[
phi*0.5 + res*0.001*#2[[2]] > 862*cutangle*Degree // N, #1,
0]
] &, data, {2}], 1], 1000
], #1[[3]] == #2[[3]] &
]
];
listloc =
Flatten[ParallelMap[MakeProfile[#[[1]], #[[2]]] &, listloc], 1];
maxloc = Max[listloc];
Select[listloc, #[[3]] > 0.2*maxloc &]
]
以下のように簡単にツリー構造として表すことができます。
TreeForm@Hold@Module[...]
WLのいいところ
部分式を即評価できる。
WL言語は上図のように木構造になっており、その枝にあたる部分式はすべてもとの式同様に評価できます。なのでどんな複雑なプログラムも、小さな部分式に分解して評価してみれば全体の動きをつかむことができます。
たくさん型を覚える必要がない
WLはオブジェクト指向のように、たくさんの型を覚える必要がありません。WLには基本的に原子式とリストしかなく、たまにGraphicsとかImageなどの生オブジェクトがあるだけです。
WLではGraphicsとかImageなど、必要なものだけが厳選されて生オブジェクトとして、ライブラリから提供されています。この生オブジェクトは中身がどうなっているかわからないですが、生オブジェクトと会話する関数がいくつも用意されているので、それで十分です。
シンタックスシュガーが便利
WLには便利なシンタックスシュガー(SS)がいくつかあります。これらのSSは、すべて基本形式に変換されます。
カッコを使わず関数を作用させる//と@#
まず、//と@です。これらはカッコを使わずに関数を作用させることができます。
例えばa//fはf[a]という意味で、またf@aはf[a]という意味です。
これがなぜ便利かというと、プログラムを作ってるとき、ある部分に関数を作用させたりさせなかったりしたいときがあると思いますが、このときf[a]という書き方だと、関数を作用させるとき、f[と]が離れたところにあるので、f[を入力して、カーソルを動かして、式の後ろに]を入力するという作業にが必要です。また関数を取り除くとき、これと逆の作業をする必要があります。//や@を使えば、注目する式の後ろか前に//f、f@をつけるだけなので、カーソルを動かす必要がありません。これがすごい便利です。
pythonのreduce,mapに相当する@@,/@
Plus@@{a,b,c} はa+b+cになります。
f/@{a,b,c}は{f[a],f[b],f[c]}になります。
lambda式#、&
WLでは純関数と呼ばれています。
#^2&は入力を二乗する関数を表します。なので#^2&[a]はa^2となります。
さきほどの/@と合わせてつかうと、#^2&/@{a,b,c}は{a^2,b^2,c^2}となります。この使い方はよくします。
配列のスライス;;
a[[i;;j]]はaというリストのi番目からj番目の要素を取り出します。
a[[i;;j;;k]]はaのi番目からj番目をk個飛ばしでとります。
他にもいろいろな取り出し方ができます。
リスト操作関数が強い
pythonのmapは一次元リストを前提としてますが、WLでは多次元リストに対してどのレベルまでMapを作用させるかを指定できます。例えばf/@{{a,b},{c,d}}は{f[{a,b}],f[{c,d}]}になりますが、レベル指定をしたMap[f,{{a,b},{c,d}},{2}] は{{f[a],f[b]},{f[c],f[d]}}になります。リストのネストしたカッコをはずFlattenも便利です。例えばFlatten[{a,b,{c,d}}]は{a,b,c,d}になります。この関数もレベル指定ができます。
関数の引数のとり方が最先端
まず関数のオーバーロードみたいなことができます。f[a]、f[a,b]
のように、同じ名前の関数でも引数の数により異なる動作が定義できます。
次にオプション引数というものがあります。これは普段はデフォルトの値が入ってるか何も値が入ってないけど、その値を変えたいときに与えることができる引数です。例えばf[a]のbというオプションに1を入れる場合、f[a,b->1]という引数を与えます。
関数のオーバーロードだけでは変数が3つ以上になったときに無理がでてきます。
例えばf[a,b,c]のaがメインの入力で、b,cがオプション的な入力のとき、bはデフォルトのままで、cにxを与えるというとき、オーバーロードだけだと、bの入力を省略することができません。WLならばこれは、f[a,c->x]というふうにかけるわけです。
任意数の引数は関数を定義を通常はf[x_]:=とするところを、f[x__]:=とすることで使えます。
ルール&置換パラダイム
WLにはルール&置換という書き方があり、パターンに当てはまる部分式をみつけて、それを別の式で置き換えるということができます。例えば、f[a]/.a->bはf[a]という式からaというパターンをみつけ、それをbに置き換えるという意味です。よってf[a]/.a->bはf[b]になります。プログラムとしての式にこれを使えばマクロのような使い方ができ、データとしての式にこれを使えば、データ操作の手段として使えます。またこれを使えば文字式として変形していって最後に値を入れるという使い方もできます。
シンボルの属性によって関数の振る舞いを変えれる。
例えばa+(b+c)=a+b+cであることは基本形式ではPlus[a,Plus[b+c]]がPlus[a,b,c]と変形されることを意味します。WLでは、PlusのFlatという属性により、このような変形が自動的に行われるようになっています。またベクトルや行列の足し算ではリストのすべての要素にまとめて演算が行われますが、これはListableという属性により実現されます。また交換法則が成り立つ演算にはOrderlessという属性があり、パターンマッチのときに演算の順番が無視されて、例えばa+bとb+aは同じ式と認識されます。この属性はユーザー定義の関数にも追加できます。
低レベル関数、GUIもある。
ファイルやディレクトリの操作、バイナリファイルを読み書きもできます。
また、マウスやキーボード入力を取得したりGUI的なこともできます。
また最近はUnityと連携できるらしいです。
Pythonとの比較
すべての能力がはじめから入っている
pythonはimportでどんな能力も手に入れるという方針ですが、WLは基本的にすべての能力がはじめから入ってます。これのいいところは世界観が統一されているため、関数どうしの親和性がいいことです。ライブラリを使う場合、ライブラリごとにデータの表し方が違うので困ることがあります。例えばnumpyのリストと普通のリストは使い勝手が少し違うので面倒くさいです。
表現力が違う
pythonではmatplotlibという最強可視化ライブラリがありますが、あくまでグラフを作るライブラリです。WLでは上述したように世界観が統一されてますので、グラフを描く関数は三角形などの図形オブジェクトを作る関数の一種として扱えます。なのでグラフ上に図形を描くということも簡単にできます。またグラフや図形をインタラクティブに操作できるようにすることもできます。これはグラフ描画ライブラリ、図形描画ライブラリ、GUIライブラリがはじめから協力プレイする前提で入っているということです。
コードの一部をコンパイルできる!
pythonもWLも型判定をなくしたかわりに速度を犠牲にしています。しかしWLではCompileという関数でコードの一部を機械語にコンパイルできます。pythonではcythonで同じようなことをできますが、やはり世界観が統一されてない影響で面倒くさくなっています。WLでは関数でこれができます。
WLの微妙なところ
カッコが普通と違う
WLでは[]が関数のカッコで、[[]]が配列のカッコです。数式を自然に表現するために仕方なくこうなりました。[[]]はWolfram言語最大の汚点です。カッコの記号がもう一つ多ければこんなことにはなりませんでした。
カッコが多い。
いろいろなSSでカッコを減らすことはできますが、大きいプログラムになるとカッコは増えていきます。Mathematicaではカッコは自動インデントされるのでいいですが、自動インデントがなかったらきついかもしれません。
普通のプログラムを書くためのしきたりを覚える必要がある。
WLではc言語のように手続き型のプログラムを書くことができますが、if文や、forループ、関数の定義、ローカル変数などは言語の文法として用意されておらず、その機能を可能にするシンボルを使って式を構築します。例えば以下のc言語のコード
int func(int n){
int i,r=0;
for(i=1;i<n;i++){
r+=i*i;
}
return r;
}
はMathematicaで以下のようになります。(型は適当です)
func[n_]:=Module[{i,r=0},
For[i=0,i<n,i++,
r+=i*i;
];
r
]
これの基本形式は以下のようになります。
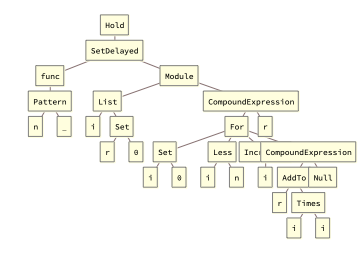
WL言語では、普通のプログラム言語ではコンパイラが構文解析して生成する木構造を、直接入力として与える感じになります。SSのおかげでぱっと見似たようにかけるというだけで、実際にはWLに手続き型プログラムに関する文法はありません。これがはじめての人には戸惑うかもしれません。
いろいろな役割のシンボルを覚える必要がある
WLのシンボルは、Plus,Timesなどの関数としての意味をもつシンボル、Integer,Stringなどの型を意味するシンボル、Graphics,Imageなどオブジェクトとしての意味をもつシンボル、For,Moduleなどの手続きプログラムのためのシンボル、True,Allなどのラベルとしてのシンボルがあり、その役割の違いがわからないと混乱するかもしれません。
パターンと関数の役割がかぶる
リストの中からある条件に満たす要素を探すとき、条件をパターン記法で表す方法と、真偽値関数で表す方法があります。WL組み込み関数のCasesとSelectはこの2つの記法に対応していますが、実質的に同じことををする関数が2つあるので”純粋”ではないという感じがします。実際、組み込み関数FirstPositionはパターン記法ですが、これの真偽値関数を使うバージョンはありません。
正直、WLをより完璧にするには、CasesかSelectを一つにして両方の記法を受け取れるようにすべきだと思います。そして同じことをPositionやFirstPositionなどにもするべきだと思います。
結論
WLは最も優れたプログラム言語である。