これは何?
これは MEGAZONE 株式会社 のテック陣「MEGAZONEのゆかいな仲間たち」がおくる、Megazone Japan Advent Calendar 2023 の十日目のエントリーです。
はじめに
みなさーん、Step Functions を有効活用してますかー? re:Invent 2023 では Step Functions に関する機能アップデートも発表されましたが、ここではそんなことに一切触れずに我が道を進みます。
普段、業務で Step Functions を扱うとき、ほとんどのケースでは Enterprise 領域のお客様から「ジョブ管理システムを AWS の機能でなんとかできないものか?」といった相談を受けて、Step Functions を提案したります。でも、Enterprise 領域のお客様って、既にオンプレでJピー(伏せ字)1などの本格的なジョブ管理システムを使って、バッキバキにジョブネットを組んでたりするので、Apple to Apple な移行をしようとすると地獄を見ることもあります。
そんなこんなで、実際の業務では Step Functions に対して挫折感しか覚えてませんが、それでも AWS のサービスの中で Step Functions は好きなサービスの1つでもあります。何故か男の子心をくすぐるポテンシャルを持ってそうな匂いを感じるんです。不思議ですね。
男の子心をくすぐると言えば、マリオメーカー計算機が有名ですが、今年はゼルダの伝説でティアキン論理回路が話題になっていました。(ほんと?)
そう! 時代はゲームによる論理回路戦国時代! 乗るしかない、このビッグウェーブに! (表現が古くて、ほんとすまん)
でもここは Megazone Japan Advent Calendar 2023 のエントリーであり、「MEGAZONE株式会社のテックエンジニア陣が自分達の技術力をささやかにアッピールしてみるカレンダーです。」と書いてある以上、業務に関係ないゲームを題材に扱うわけにはいかないので、Step Functions で論理回路をの話をしたいと思います。
Step Functions で論理回路
Step Functions の Choise ステートには And, Or, Not の比較演算子が用意されています。はい、論理回路が大好きな諸兄姉はピン!と来たかと思いますが、これで加算器が作れそうな気がします。
加算器の回路図についてはググれば色々と出てきますので、ここでは割愛します。
ということでまずは半加算器に必要な論理ゲートを作ってみます。
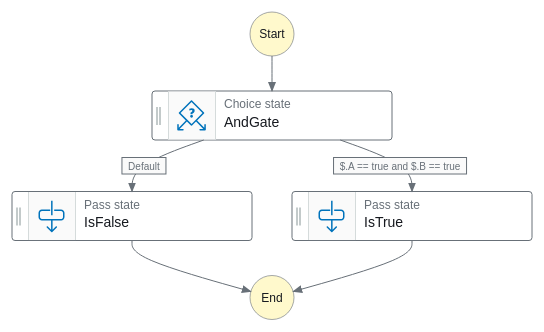
AND ゲート
諸兄姉には釈迦に説法になりますが、一応お約束の真理値表を貼ります。A と B が入力で S が出力です。
| A | B | S |
|---|---|---|
| F | F | F |
| T | F | F |
| F | T | F |
| T | T | T |
図としてはこんな感じになります。
定義はこんな感じです。入力が両方とも True のときだけ True を返せばいいので、それ以外のパターンは全部 False を返す内容です。
{
"Comment": "AND Gate",
"StartAt": "AndGate",
"States": {
"AndGate": {
"Type": "Choice",
"Choices": [
{
"And": [
{
"Variable": "$.A",
"BooleanEquals": true
},
{
"Variable": "$.B",
"BooleanEquals": true
}
],
"Next": "IsTrue"
}
],
"Default": "IsFalse"
},
"IsFalse": {
"Type": "Pass",
"Result": {
"S": false
},
"End": true
},
"IsTrue": {
"Type": "Pass",
"Result": {
"S": true
},
"End": true
}
}
}
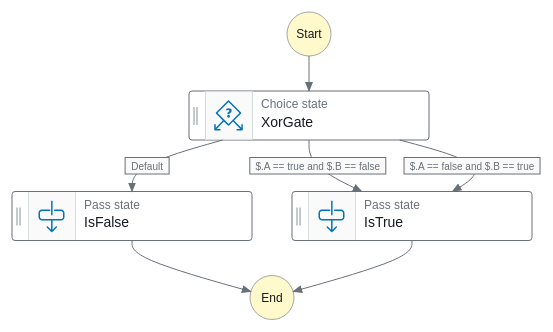
XOR ゲート
一応お約束の真理値表を貼ります。A と B が入力で S が出力です。
| A | B | S |
|---|---|---|
| F | F | F |
| T | F | T |
| F | T | T |
| T | T | F |
図としてはこんな感じになります。
定義はこんな感じです。入力が True と False のペアのときだけ True を返せばいいので、それ以外のパターンは全部 False を返す内容です。
{
"Comment": "XOR Gate",
"StartAt": "XorGate",
"States": {
"XorGate": {
"Type": "Choice",
"Choices": [
{
"And": [
{
"Variable": "$.A",
"BooleanEquals": true
},
{
"Variable": "$.B",
"BooleanEquals": false
}
],
"Next": "IsTrue"
},
{
"And": [
{
"Variable": "$.A",
"BooleanEquals": false
},
{
"Variable": "$.B",
"BooleanEquals": true
}
],
"Next": "IsTrue"
}
],
"Default": "IsFalse"
},
"IsFalse": {
"Type": "Pass",
"Result": {
"S": false
},
"End": true
},
"IsTrue": {
"Type": "Pass",
"Result": {
"S": true
},
"End": true
}
}
}
半加算器
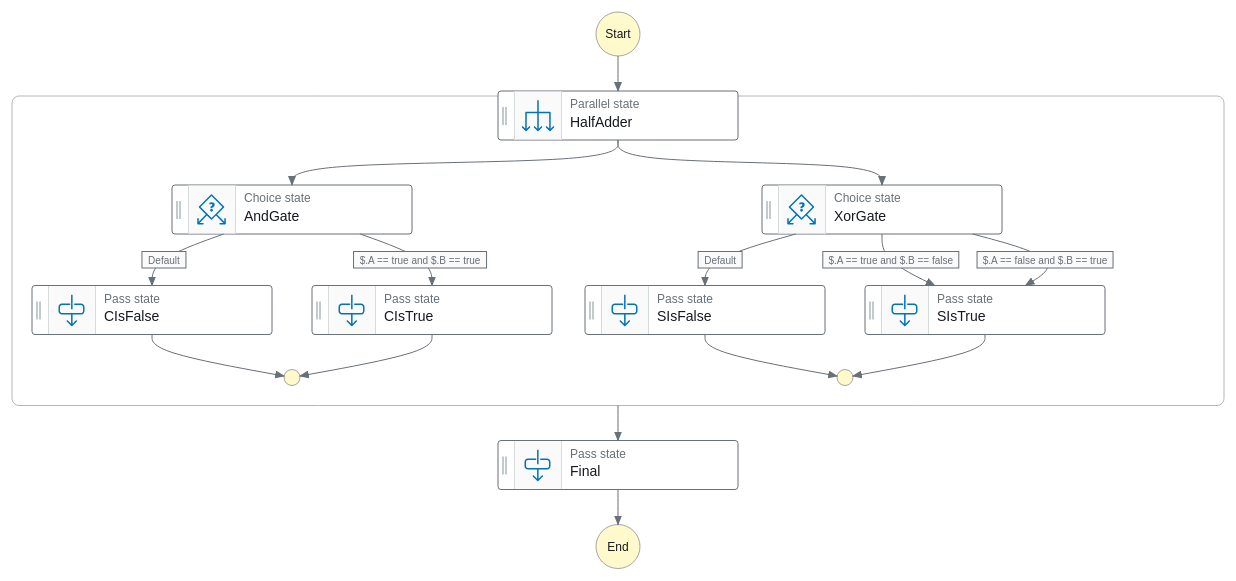
さて、AND ゲートと XOR ゲートが揃ったところで、いよいよ半加算器の作成です。
AND ゲートと XOR ゲートを組み合わせるとこんな感じの図になります。
はい。半加算器だけなのに、ちょっと嫌な予感がしますよね。そうです、このまま半加算器を組み合わせて全加算器を作ろうとすると…ちょっとかなりごちゃごちゃしそうですよね。
ところで半加算器の真理値表を貼ります。A と B が入力で C と S が出力です。C は繰り上がりを示します。
| A | B | C | S |
|---|---|---|---|
| F | F | F | F |
| T | F | F | T |
| F | T | F | T |
| T | T | T | F |
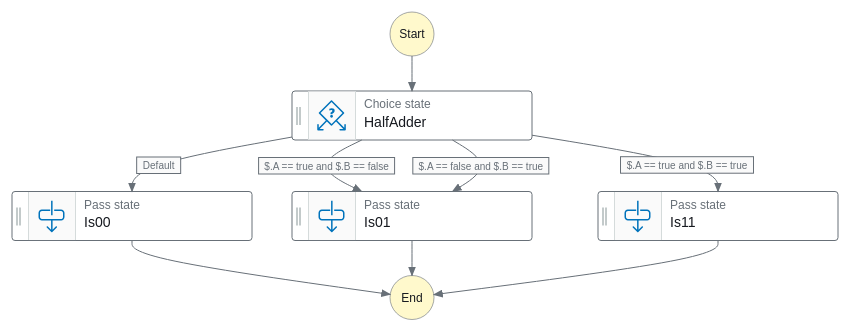
はい、気付いたと思いますが、XOR ゲートの出力に C が増えただけですので、ぶっちゃけ XOR ゲートのコードに繰り上がりの部分を書くだけで済みます。図とコードは以下のようになります。
{
"Comment": "Half Adder",
"StartAt": "HalfAdder",
"States": {
"HalfAdder": {
"Type": "Choice",
"Choices": [
{
"And": [
{
"Variable": "$.A",
"BooleanEquals": true
},
{
"Variable": "$.B",
"BooleanEquals": true
}
],
"Next": "Is11"
},
{
"And": [
{
"Variable": "$.A",
"BooleanEquals": true
},
{
"Variable": "$.B",
"BooleanEquals": false
}
],
"Next": "Is01"
},
{
"And": [
{
"Variable": "$.A",
"BooleanEquals": false
},
{
"Variable": "$.B",
"BooleanEquals": true
}
],
"Next": "Is01"
}
],
"Default": "Is00"
},
"Is00": {
"Type": "Pass",
"Result": {
"C": false,
"S": false
},
"End": true
},
"Is01": {
"Type": "Pass",
"Result": {
"C": false,
"S": true
},
"End": true
},
"Is11": {
"Type": "Pass",
"Result": {
"C": true,
"S": true
},
"End": true
}
}
}
だいぶダルいですね… f^^;
全加算器
さて、半加算器が作れたので、いよいよ全加算器の作成です…といきたいところですが、半加算器のときのように、半加算器を使い回すようにしようとすると、ひとつめの半加算器は入力が A, B ですが、ふたつめの半加算器は入力が S と C になります。つまり AND ゲートと XOR ゲートを Parallel ステートくくって作ろうとしたときのような方法が取れません。すると、ひとつめの半加算器のあとに分岐処理で「ひとつめの処理か否か」を判断し、ひとつめの処理の場合はもう一度半加算器に処理を戻してその際の入力値はひとつめの半加算器の出力 S と、入力 C を処理し… 面倒臭い…orz
一応、お約束の真理値表を貼ります。
| Ci | A | B | Co | S |
|---|---|---|---|---|
| F | F | F | F | F |
| F | F | T | F | T |
| F | T | F | F | T |
| F | T | T | T | F |
| T | F | F | F | T |
| T | F | T | T | F |
| T | T | F | T | F |
| T | T | T | T | T |
あぁ…なんか半加算器のときのように Choice ステートで And で全部誤魔化したい…。
さて、ここでどう進めるか悩みどころですが、さすがに論理回路が好きな諸兄姉でも「Step Functions にある組み込み関数の States.MathAdd を使えばいいんじゃね?」と思うわけですがそんなことを言ったらいつまでも成長できません。人類の歴史は常に困難の挑戦によって作られてきたのですよ。
ということで、このシリーズ続くかどうかわかりませんが、次回があるようであれば、分岐処理によって半加算器を有効活用するコードを書くことを目指します。
投稿後…
すでに2年前に Fusic さんの Tech Blog で StepFunctionsだけで無駄に壮大な4bit加算器を作ったよ
という記事があることに気付きました…orz
さすが Fusic さん、マジパネぇ…
ということで、このシリーズは先駆者が居たので、ちょっと Fusic さんの記事を読んで修行に励みます。