More than 5 years have passed since last update.

SFC版風来のシレンの乱数生成アルゴリズムの話考察編

Last updated at 2017-12-04Posted at 2017-12-02

この記事は続編です。
前回の記事で、SFC版風来のシレンのROMデータの解析内容を元に乱数がどのようにして生成されているかを解説しています。そちらを読んでからこの記事を読んでいただくと、より内容を理解しやすいかと思います。

前回の記事：SFC版風来のシレンの乱数生成アルゴリズムの話解析編

#SFC版風来のシレンの乱数の品質を調べる
さて前回の記事でSFC版風来のシレンの乱数生成アルゴリズムが線形帰還シフトレジスタの一種であることが分かりました。

しかし乱数生成アルゴリズムは理解したものの、それによって生成された乱数が妥当な物なのかというのはアルゴリズムを見ただけでは分かりません。
シレンの乱数は偏りやすいと断言できるような目に見えて質が悪いものなのでしょうか。
この項でそれを考察してみたいと思います。

先にお断りしておきますが、本気で定量的・客観的に乱数の品質を検証しようと思うと本格的な統計学などの知識が必要になるはずです。しかしあいにくそこまでの知識は持ち合わせていません。
また乱数の品質を検証するソフトも存在しますが、使い方を調べるのが面倒くさい（おい）のと、シレンのような0-255という狭い範囲の値が生成される乱数に適用できるのかどうかもよく分からないので、そういったものの利用も今回はパスします。

以下では統計学の素人でも検証・理解できるレベルで、かつ質の悪い乱数の特徴が現れやすい項目を調べます。

再掲：C言語による風来のシレンの乱数生成アルゴリズム互換ルーチン

前回のエントリーで掲載したC言語による風来のシレンの乱数発生アルゴリズムの互換ルーチンを再度掲載します。
今回は実際にこちらのルーチンを使用して乱数発生アルゴリズムの質を見ていくことにします。

#include <stdint.h>

#define SIREN_RNG_INIT_STATE 0xf7e8dd05
uint32_t siren_rng_state = SIREN_RNG_INIT_STATE;

uint8_t siren_rng_next()
{
    uint32_t result =
        ((siren_rng_state & 0x7f800000) >> 23) ^
        ((siren_rng_state & 0x0003fc00) >> 10);

    siren_rng_state <<= 8;
    siren_rng_state |= result;

    return (uint8_t)result;
}

乱数の周期は十分に大きいか

過去の乱数から次の乱数を生成する擬似乱数生成器は必ず周期性を持ちます。
乱数生成の元となる状態変数の取りうる値は有限なので、乱数を次々と生成していく仮定でいつかは状態変数が以前に乱数を発生させた時の値と同じになります。そうなると、そこから後は以前と全く同じ乱数列が発生することになり、周期性が出るわけです。
この周期の長さは乱数の品質を決定するうえで重要な要素になります。乱数列の周期が短いとその分同じ乱数列を使用する回数が増えるため、同じ展開が発生しやすくなってしまいます。逆に周期が長ければ同じ乱数列を使用する機会が減るため同じ展開が発生しにくくなります。
最近の高品質とされる乱数は周期が天文学的に長い¹ため乱数列を周回することは事実上起こらないので、乱数を消費しつづけても同じ乱数列が現れることがありません。

SFC版風来のシレンの乱数の周期

では風来のシレンの乱数生成アルゴリズムの周期はどのくらいなのでしょうか。
数学に詳しい人ならアルゴリズムから導けるのでしょうが²、私にはそこまで専門的な知識はありません。ですが幸いな事に風来のシレンの乱数の状態変数は過去4回の乱数の値なので8ビットx4=32ビット、つまり状態変数の取りうる値は$2^{32}$通りです。過去と同じ状態変数が現れた時点で周期性が発生するのですから、乱数の周期は高々$2^{32}$となり、コンピュータの計算量としてはそこまで大きなものではありません。これなら実際に乱数を発生させつづけて過去と同じ状態変数が現れるまでの回数をカウントする力技で十分です。

#include <stdio.h>

int main()
{
    uint32_t counter = 0;
    do {
        siren_rng_next();
        counter ++;
    } while (siren_rng_state != SIREN_RNG_INIT_STATE);

    printf("%d\n", counter);

    return 0;
}

なんのひねりもないですが上のようなプログラムを組んで実行してみました。(ついでにtimeコマンドで実行にかかった時間も計測、実行環境はCPU Core-i7 2700K、VirtualBox上のUbuntu 17.04です。)

% time ./a.out 
2147483647
./a.out  3.18s user 0.00s system 99% cpu 3.196 total

**周期は$2147483647$、すなわち$2^{31}-1$**になりました。大規模な科学技術シミュレーション等に使用するのにはさすがに物足りないですが、ゲームで使用する乱数としては十分と言えそうです。
前回シレンの乱数生成アルゴリズムはXorshiftに似ていると言いましたが、Xorshift系（線形帰還シフトレジスタ）のアルゴリズムは状態変数が$n$ビットの場合周期は最大$2^n-1$になる事が知られています。
最大の$2^{32}-1$にこそなりませんでしたが、周期に関しては割と頑張っているのではないでしょうか。SFC時代にここまで大きな周期の乱数を使っているゲームは他にはあまりないように思います。

他のゲームの乱数の周期の例

他の割と有名どころのゲームの乱数の例をあげてみます。

例えばSFCのファイナルファンタジー4・5・6は0-255を不規則に256個ならべた乱数テーブルと毎フレーム0-255を1ずつカウントアップする(255の次は0に戻る)カウンタを使用して乱数を生成しています。乱数が必要となったときに乱数テーブルの参照位置を後者のカウンタの値だけ進め（無論テーブルの最後を超えたら先頭に戻る）、その値を使用するといった具合になっているようです。
この方式だとプレイヤーのコントローラ入力が起点となって単発で乱数が生成される場合は、入力のタイミング次第でカウンタの値が0-255のいずれになる可能性もあるので、乱数テーブルの参照位置はテーブル上のどの位置になる可能性もあり、真の乱数に近いと言えます。
しかしプレイヤーの入力が間に入らず連続的に乱数の生成が必要になった場合、プログラムの処理速度は一定のため一連の乱数の必要になるタイミングが固定されてしまいます。そうなると乱数列の最初の乱数が生成されたタイミングでの乱数テーブルの参照位置(256通り)とカウンタの値(256通り)の組み合わせで完全に得られる乱数列が決定されるので、その乱数列の種類は$256*256=65536$通り、つまりFF4-FF6の**乱数の周期は$2^{16}$**しか無いことになります。
とはいえ、RPGは元々乱数に大きく左右される要素が少ないゲームですから周期が$2^{16}$程度確保されており乱数の出目にあからさまな瑕疵がなければとりあえず問題はないでしょう。
FF4-6に限らずこの頃のゲームの乱数の周期は$2^{16}$程度のものが多いのではないでしょうか。

さらに悪い例もあります。SFC版ファイアーエムブレム紋章の謎は0-99が不規則に256個並んだ乱数テーブルをそのまま順番に参照して乱数として使用しています。すなわち**乱数の周期はたったの$256$**です。³

こういったゲーム達に比べれば風来のシレンの$2^{31}-1$というのははるかに大きな周期であり、乱数の消費が激しいローグライクゲームの乱数の周期としてもまず及第点といえるのではないでしょうか。

余談：状態変数の初期値の選択

乱数の質とは直接関係ありませんが、周期の話と関連するのでここで状態変数の初期値についてとりあげます。
一般的に、擬似乱数を使用する時は一番最初に状態変数の初期値を与えます。初期値には通常自然的に刻々と変化している値（例えば/dev/urandamの値やtime()関数の戻り値など）を使い、最初に生成される乱数列が固定されてしまわないようにします。
シレンの乱数発生アルゴリズムの状態変数の初期値も適当にそのような値を与えておけばよいのでしょうか。

必ず避けなければいけない初期値

乱数生成ルーチンを再度見てください。状態変数siren_rng_stateの初期値が0だった場合どうなるでしょうか。32bitの0の並びからどう8bitを取り出しても0ですし、それをいくらシフトしようが、XORを取ろうが0のままです。したがって生成される乱数も0になり、当然ながら次の状態変数の値も0になります。つまり状態変数の初期値が0の場合乱数の値が0で固定されてしまうということです。
Xorshift（線形帰還シフトレジスタ）のアルゴリズムはシフトとXORしか使用しないので状態変数の全ビットが0の場合こうなることが知られています。したがって状態変数の初期値を決める時には全ビットが0になるのだけは避けるように注意しなければなりません。線形帰還シフトレジスタの一種である風来のシレンの乱数生成アルゴリズムも同様というわけです。
先程状態変数が$n$ビットのXorshift系アルゴリズムは周期が最大$2^n-1$になると書きましたが、この$-1$は状態変数の全ビットが0の場合が含まれないため必然的にそうるわけです。

周期上に現れない状態変数を初期値に選んでよいか

さて、先程シレンの乱数生成アルゴリズムは周期が$2^{31}-1$になる事を実証しました。状態変数の取りうる値は$2^{32}$通りですが、初期値がこの周期に含まれる$2^{31}-1$通りの値のどれかであれば以降状態変数はその$2^{31}-1$通りの値で循環します。初期値が0だった場合は状態変数は0で固定されます。
では、初期値として残りの$2^{31}$通りを選んだ場合どうなるのでしょうか。
ここで、状態変数siren_rng_stateの最上位ビットに注目します。状態変数の最上位ビットは次の乱数の生成には使用されていません。また、乱数生成後に状態変数は左に8bitシフトされるため最上位ビットは消えてしまうので、次の状態変数の値にも影響を及ぼしません。
したがって、状態変数の最上位ビットは0だろうが1だろうが残りのビットが同一であれば生成される乱数に変わりはないし、次の状態変数の値は同じになるということになります。
すなわち、状態変数$x$に乱数生成アルゴリズムを適用した時に次の状態変数を生成する関数を$f(x)$とし、上述の周期$2^{31}-1$の乱数列上の任意のn個目の状態変数の値を$s_n$とすると、

s_{n+1} = f(s_n)…①

と定義できますが、この時$s_n$の最上位ビットを反転させた値を$s'_n$とすると、

s_{n+1} = f(s'_n)…②

が成り立つことになります。

では$s'_n$が周期的な乱数列上の$2^{31}-1$通りの状態変数の値のいずれかになる事はあるでしょうか。
答えは否です。背理法で証明できます。
$s'_n$が周期上の状態変数に含まれると仮定します。すると①、②により周期上に含まれる別々の状態変数の値$s_n$,$s'_n$から同じ状態変数の値$s_{n+1}$に変化することになります。これは周期上で同じ状態変数の値が複数存在しない（そこで周期がくずれてしまうため）という前提に矛盾します。したがって仮定が正しくなかったことになり、周期的な乱数列上の任意の状態変数の値$s_n$の最上位ビットを反転させた$s'_n$は、同じ乱数列上の状態変数の値として存在しない事が証明できました。

これらの事により、$2^{32}$通りに取り得るの状態変数の値の内訳は

周期的な乱数列上に現れる$2^{31}-1$通りの値
それらの最上位ビットを反転させた、周期的な乱数列上に現れない$2^{31}-1$通りの値
0
0x80000000(0の最上位ビット反転)

となります。
そしてリストの2番目の「周期的な乱数列上にない状態変数の値$s'_n$」を初期値に選んだ場合、②により1度乱数生成アルゴリズムを適用するとリストの1番目の「周期的な乱数列上の状態変数の値$s_{n+1}$」になることがわかっているので、その後は周期的な乱数列上を循環することになります。
0x80000000を初期値に選んだ場合は次の状態変数は0となり、当然乱数も0に固定されます。

以上により、風来のシレンの乱数生成アルゴリズムは状態変数の初期値として0、0x80000000を除くいかなる値を選択しても問題はないことになります。

では実際に風来のシレンではどのように乱数の初期化をしているかですが、前述の解析サイトを見ても書いておらずどうなっているのは分かりませんでした。機会があれば調べてみたいところです。

ところで、風来のシレンの乱数の周期が$2^{31}-1$になったのはこの状態変数の最上位ビットが次の乱数生成に寄与してないためといえます。状態変数として意味があるのが最上位ビットを除いた31ビットなので、どう頑張っても$2^{31}-1$になるわけです。つまり最上位ビットが次の乱数生成に使われるように乱数生成の計算式にうまく組み込めれば、最大となる$2^{32}-1$の周期が実現できそうな気がしますがどうなんでしょうね。
ただ、アルゴリズムは速度も重要なので計算が増えて処理速度が遅くなってしまっては本末転倒です。周期$2^{32}-1$が実現できても周期がせいぜい倍になるだけですから、周期の長さと計算量のバランスを考えてあえて周期$2^{31}-1$にしている可能性もあります。

長期的に見た乱数の値の偏りはあるのか

よくある「プログラム上の攻撃を外す確率は1/8なのに体感ではもっと外れている⁵」というような意見が事実なら、例えば「6の目が他の目より出やすいサイコロ」のように、乱数のすべての出目が均等に出ず偏っていることになります。
実際の所シレンの乱数生成アルゴリズムは、長期的に見て乱数の出目に偏りがあるのでしょうか。

ROMを解析した方のサイトでは実際に16777216回乱数を発生させて0-255がそれぞれ生成された回数を調べており、大体どの値においても同じような回数出現していることを示しています。

この例で十分に乱数の出目に偏りはないといえると思いますが、折角なのでここでは周期の回数だけ乱数を生成して0-255が出る回数をそれぞれ数えてみましょう。

#include <stdio.h>

int main()
{
    uint32_t result_count[256] = {0};
    int i;
    do {
        result_count[siren_rng_next()] ++;
    } while (siren_rng_state != SIREN_RNG_INIT_STATE);

    for (i = 0; i < 256; ++ i) {
        printf("%d = %d\n", i, result_count[i]);
    }

    return 0;
}

これまたなんのひねりもありません。では実行してみます。

% time ./a.out
0 = 8388607
1 = 8388608
2 = 8388608
3 = 8388608
4 = 8388608
5 = 8388608
6 = 8388608
7 = 8388608
（略）
255 = 8388608
./a.out  3.49s user 0.00s system 99% cpu 3.503 total

見ての通り、1-255が全く同じ回数の$8388608=2^{23}$回ずつ生成され、0がそれより1だけ少ない$2^{23}-1$回生成されました。0が出る回数が1だけすくないのは、状態変数の初期値が全ビット0で乱数が0に固定される場合が除かれているためです。
これはXorshift（線形帰還シフトレジスタ）の乱数生成アルゴリズムの特徴と同様であり、Xorshiftをはじめ他のバリアントもおなじ結果になるのではないかと思います。

結論としては、シレンの乱数の出目は長期的に見て、厳密にはごくごく僅かに0が他より出にくいものの、ほぼ全くといってよいレベルで偏りはなく全ての出目が均等に出現すると言えます。

短期的な偏りの発生率は妥当か

今度は逆にシレンの乱数生成アルゴリズムの乱数の出目の短期的な偏りが妥当なものか見てみます。
例えば「攻撃が外れるときは連続して外れやすい」といった主張が正しいのであれば、一定範囲の乱数値が連続して発生する率が計算上の期待値より大きくなっている事になります。また、前述のSFCファイアーエムブレム紋章の謎のように、乱数列に大小交互の値が出るような規則的な傾向があれば逆に同じ現象が連続する率が期待値より小さくなりそうです。

以下のようなプログラムで1周期中に生成した乱数の値が連続して指定した条件を満たした回数をカウントしてみます。
（これも解析した方のサイトで周期より少ない回数ではありますが、実際に生成した乱数で同様の検証をやっておられます。）

#include <stdio.h>

static int cond(uint8_t rng_result)
{
    return ((rng_result & 0x7F) >= 0x70);
}

int main()
{
    uint32_t seq_count[12] = {0};
    int seq_counter = 0;
    int i;
    do {
        uint8_t rng_result = siren_rng_next();
        seq_counter = cond(rng_result) && seq_counter < 11 ?
            seq_counter + 1 : 0;
        seq_count[seq_counter] ++;
    } while (siren_rng_state != SIREN_RNG_INIT_STATE);

    for (i = 0; i < 12; ++ i) {
        printf("%d = %d\n", i, seq_count[i]);
    }

    return 0;
}

上記のプログラムの指定した条件（cond関数）は攻撃が外れる条件（確率$1/8$）としています⁶。

実行した結果は以下のようになりました。

0 = 1879048191
1 = 234881024
2 = 29360128
3 = 3670016
4 = 458752
5 = 57344
6 = 7168
7 = 896
8 = 112
9 = 14
10 = 2
11 = 0
./a.out  5.02s user 0.00s system 99% cpu 5.021 total

これまた綺麗な結果になりました。
$n$回連続して攻撃を外す確率は$n-1$回連続して外す確率の$1/8$にほぼキッチリなっていることがわかります。期待値通りです。（生成される回数が1少ない乱数の出目0の時に条件が成立するか否か、周期の切れ目で条件が連続しているか否かで、キッチリ1/8になる場所、わずかに1/8からずれる場所が変化しそうです）

これも線形帰還シフトレジスタの特徴のようです。Wikipediaから引用：

1と0は連続して出現することがある。例えば、出力ストリーム 0110100 は5つの連続から構成されていると見ることができ、その長さは順に 1,2,1,1,2 である。最長LFSRの1周期には $2^{n-1}$ 個の連続が出現する（例えば、6ビットのLFSRでは32個の連続がある）。そのうち $1/2$ は長さが1、 $1/4$ は長さが2ビットで、0の最長の連続は $n-1$ ビットであり、1の最長の連続は $n$ ビットが1回だけある。これは真の乱数の統計的特性と全く同じである。

結論としては、短期的にみた場合、シレンの乱数の出目は計算上の期待値通りに偏ることがあり、期待値以上に偏ったり、期待値に比べて偏りがすくなかったりすることはない、妥当なものだといえそうです。

多次元に均等に分布するか

一見乱数が均等に出現しているように見えても、多次元的に配置すると偏りが発生する事があります。
一例を挙げると、単純な線形合同法で発生させた乱数列$r_0$,$r_1$,$r_2$,$r_3$…を$(r_0,r_1)$,$(r_1,r_2)$…と平面座標のデータにしてプロットしてみると規則的な模様が現れることが知られています。
このような乱数は多次元的に使用するのには向きません。例えば8bitの乱数値を2個発生させてくっつけて16bitの値として扱う、といったことをするとその値には偏りが発生してしまいます。

この点についてシレンの乱数生成アルゴリズムはどうなのでしょうか。
上述の例と同様に連続的に生成した20000個の乱数値から10000点分の平面座標のデータを作成してデータ点をプロットしてみると、次の画像のようになりました。

見たところ規則的な様子は無く、平面全体に不規則かつ均等に分布していると言えそうです。
シレンの乱数生成アルゴリズムは、すくなくとも2次元的な配置では均等に分布すると言ってよさそうです。
これなら例えば2回続けて生成した乱数をシレンやモンスター、アイテム等の配置位置の座標に使用しても偏りは発生せず安心です。

他のゲームの乱数生成アルゴリズムの例

この項について他のゲームの例を挙げてみます。

時代はだいぶ下って、ニンテンドーDS世界樹の迷宮の例。初代世界樹の迷宮は次のようなシンプルな線形合同法で乱数を生成していることが解析されています。

r_{n+1} = (r_n * 109 + 1021) \bmod 65536

生成される乱数の値は16bitで0-65535です。ちょっと問題なのは偶数で割った余りを使っているため、必ず奇数と偶数が交互に生成されます。せめて割る数を65535にするほうが良いのではないかと思いますが、2バイトデータの計算時のオーバーフローで自然と$2^{16}$で割った余りが残るのを利用するためにあえてこうしているのかもしれません。この点は下位のビットを使用しないようにすることで一応回避はできます。⁷

周期に関しては、実際に乱数を生成させて確かめた所$65536=2^{16}$でこの形の単純な線形合同法としては一応最大の周期になっています。

このアルゴリズムからやはり乱数を20000個生成し、10000個の平面座標データにしてプロットしてみます。なお、データ範囲をシレンの例にあわせて0-255にしますが線形合同法の下位ビットは規則性が強く現れる問題点があるので対策として16bitの乱数値の上位8bitを使うことにします。
結果は以下のようになりました。

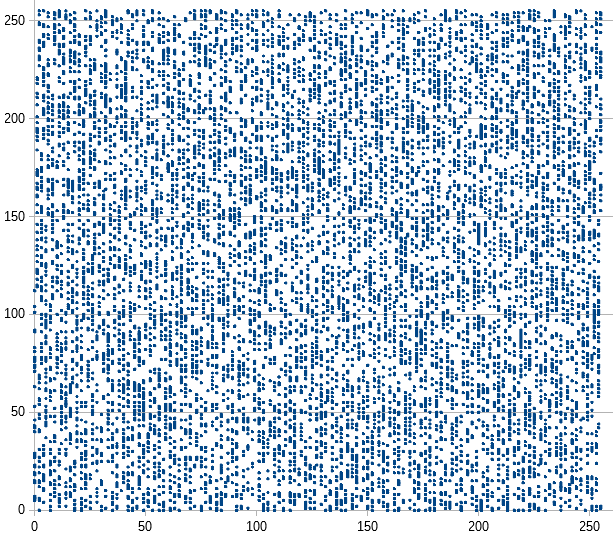
見ての通り、明らかに分布が偏っており縞模様が現れています。やはり知られている通り単純な線形合同法で生成した乱数は多次元的に使用すると偏りが発生することが分かります。

ついでですので下位8bitを使うとどうなるか見てみましょう。

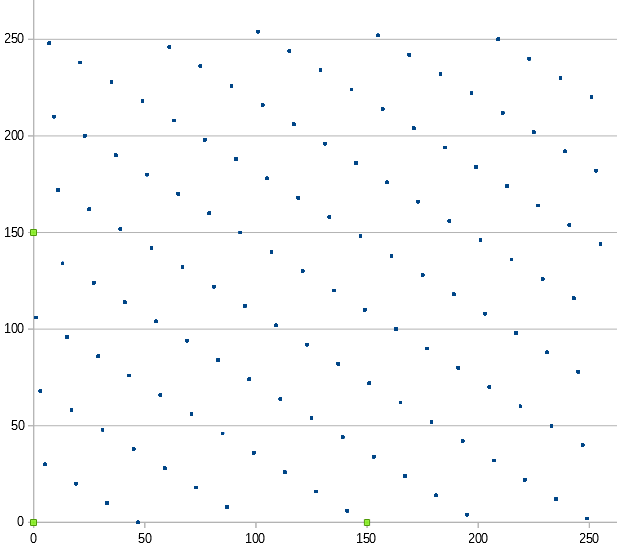
決してプロットし忘れではありません(笑)。
1万点のデータをプロットした結果こうなります。おなじ点にデータ集中してしまっています。もはや乱数とよべる代物ではありません。単純な線形合同法で生成した値の下位のビットをそのまま使ってはならないことがよくわかります。
そもそも、同じ状態変数の大きさならXorshift（線形帰還シフトレジスタ）系のアルゴリズムでもほぼおなじ周期になりますし、計算速度も掛け算や割り算が必要な線形合同法よりシフトとXORしか使用しないXorshiftに分があるので、もはや線形合同法を使用する理由は無いように思います。

まとめ

ここまで見てきたように、SFC版風来のシレンの乱数生成アルゴリズムは

ゲーム用乱数としては十分に長い周期（$2^{31}-1$）を持っている
長期的にはすべての出目が均等に出現する
短期的な偏りの発生率は期待値通りである
2次元空間に不規則かつ均等に分布する

という特徴を備えており、一般に質が悪いと言われる乱数に現れるような目立った要素はみつかりませんでした。
乱数の値に展開を大きく左右されるローグライクゲームの乱数アルゴリズムとして、十分実用に足るものであると言って差し支えないのではないでしょうか。

例えばXorshiftは$2^{128}-1$、メルセンヌ・ツイスタは$2^{19937}-1$ ↩
世の中の巨大な周期の乱数生成アルゴリズムは数学的にその乱数の周期を証明しています。 ↩
ネットでは乱数テーブルの参照ではなく線形合同法であるという記述も見られますがROMを解析したわけではないので正確には分かりません。いずれにしても周期は$256$のようです。
しかも0-99の100通りの値が256個並んでいるわけですから、当然ながらすべての値が同じ確率で出現するようになっていません。その上並びは厳密に不規則ではなく、大きめの数値と小さめの数値がだいたい交互に出現する傾向があります。
ゲーム内容自体は名作ですが、確率に支配されるシミュレーションゲームの乱数としてはいささかお粗末であると言わざるを得ません。
ここまで乱数の質が悪いとゲーム上であきらかに目に見える影響がでてくるレベルです。例えばレベルアップ時に技・幸運・武器レベルという必要性の薄いステータスばかりがまとめて上がる（俗にwkbなどと言われており割と有名な話です）といった事が起きます。⁴ ↩
力→技→素早さ→幸運→守備→魔防→HP→武器LVという順番でステータスの上昇判定が行われるため、乱数値が大小交互にでる影響で1個ずつ飛ばしたステータスが上がりやすくなってしまっています。 ↩
厳密にはシレンの直接攻撃の命中率はもう少し高いのですがとりあえずそこは置いておきます。ちなみに矢や投擲、モンスターのシレンに対する攻撃の命中率の設定は正確に7/8です。 ↩
ROM解析では、矢や投擲、敵の攻撃の命中判定は乱数の最上位ビットを0にした値が0x00-0x6Fの時に命中となっているそうです。 ↩
以前にXbox360のカルドセプトサーガで、ダイスの目が必ず奇数と偶数が交互に出るのが発覚して騒ぎになったことがありますが、上のような線形合同法で生成した乱数の下位ビットをそのまま使ってしまったのでしょうね。 ↩

110

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up

SFC版風来のシレンの乱数生成アルゴリズムの話 考察編