はじめに
Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inferenceを読みました。
この論文はTensorflow/Tensorflow Liteで実装されている、モデルのパラメータを量子化する手法です。
以前まではEdgeTPUで機械学習モデルを推論させるために、この学習方法で行う必要がありましたが、最近のEdgeTPUコンパイラのアップデートによりtensorflowのpost-training quantizationにも対応するようになりました。
post-training quantizationは学習されたモデルに対して、EdgeTPUで推論できるように量子化をする手法です。
なのでquantization aware trainingがEdgeTPUにモデルを載せるために必須ではなくなりましたが、量子化で精度を下げないように学習する手法として今後も利用されると思われます。
Contribution
この論文のContributionは以下の通りです。
- 重みと活性化関数を8bitで表現し、biasを始めとした32bit-integerの少数パラメータを利用したquantization schemeを提案
- 整数演算のみで効率的に計算できるquantized inference framework
- 量子化前のモデルとの精度の誤差を最小限にできるような量子化モデルの推論を設計するquantized training framework
- Classification, detectionタスクにおいてlatency -vs- accuracy tradeoffがMobileNetよりよかった
Quantization Scheme
本論文では量子化された値$q$と実数値$r$の対応関係を表します。
Quantization Schemeは学習時にはfloat,推論時には整数で演算することができます。
Quantization Schemeの基本構造
$$ r=S(q-Z) $$
$r$は量子化前の実数(float)で$q$は量子化後の整数(int)を表します。
$S$は$r$と$q$のスケールを調整する実数(float)です。
$Z$は$r$が0で表現されるように$q$を調整するオフセットとなります。
Quantization Schemeを利用した計算
ではQuantization Schemeを利用した計算を考えてみましょう。
$N \times N$の行列$r_1$と$r_2$あった時に$r_3 = r_1 * r_2$を計算することを考えます。
$r_1$と$r_2$は実際のニューラルネットワークでは伝搬されてきた入力値と重みに対応していています。
$r_{\alpha}$の定義は以下のようになります。
$$r_{\alpha}^{(i, j)}=S_{\alpha}\left(q_{\alpha}^{(i, j)}-Z_{\alpha}\right)$$
これを元に$r_3$を展開します。
$$S_{3}\left(q_{3}^{(i, k)}-Z_{3}\right)=\sum_{j=1}^{N} S_{1}\left(q_{1}^{(i, j)}-Z_{1}\right) S_{2}\left(q_{2}^{(j, k)}-Z_{2}\right)$$
ここで、$S$は入力の値に影響しない定数であることから推論前にオフラインで$M$を計算することができます。
$$q_{3}^{(i, k)}=Z_{3}+M \sum_{j=1}^{N}\left(q_{1}^{(i, j)}-Z_{1}\right)\left(q_{2}^{(j, k)}-Z_{2}\right)$$
$$M :=\frac{S_{1} S_{2}}{S_{3}}$$
しかし、$S$はfloatであり、推論時には$M$を整数演算として計算したいです。
$M$は試験的に計算をすると$[0,1]$の範囲となることがわかったそうです。
なので$M_0$を導入して整数演算で計算できるようにします。
$$M=2^{-n} M_{0}$$
$n$は非負の値で$M_0$は本来$[0,0.5)$ではあるが整数演算を行うためにビットシフトさせた値である。
$M$をint32と考えると$M_0 = 2^{31} M_0$と整数に変換しこの時$M_0$は少なくとも$2^{30}$の情報量を格納することができます。このように$M_0$を変換させて計算をすることにより、$M$を整数演算として考えることができます。
ここからさらに$\sum_{j=1}^{N}\left(q_{1}^{(i, j)}-Z_{1}\right)\left(q_{2}^{(j, k)}-Z_{2}\right)$を展開してみます。
$$q_{3}^{(i, k)}=Z_{3}+M\left(N Z_{1} Z_{2}-Z_{1} a_{2}^{(k)}\right.-Z_{2} a_{1}^{(i)}+\sum_{j=1}^{N} q_{1}^{(i, j)} q_{2}^{(j, k)} )$$
$$a_{2}^{(k)} :=\sum_{j=1}^{N} q_{2}^{(j, k)},a_{1}^{(i)} :=\sum_{j=1}^{N} q_{1}^{(i, j)}$$
ここで$a_{2}^{(k)}$と$a_{1}^{(i)}$はそれぞれ$N$回加算をすることで演算ができます。なのでこれらの加算回数は一つの行列積として合計$2N^2$回加算で計算することが可能なわけです。
$\sum_{j=1}^{N} q_{1}^{(i, j)} q_{2}^{(j, k)}$は整数行列の積和演算に該当する部分なので$2N^3$回積和演算が呼ばれます。しかしこの項を除いた演算は$O(N^2)$で計算をすることができます。
Quantization Schemeを利用した推論
Quantization Schemeを利用したモデルはFigure1.1の左のように計算されます。
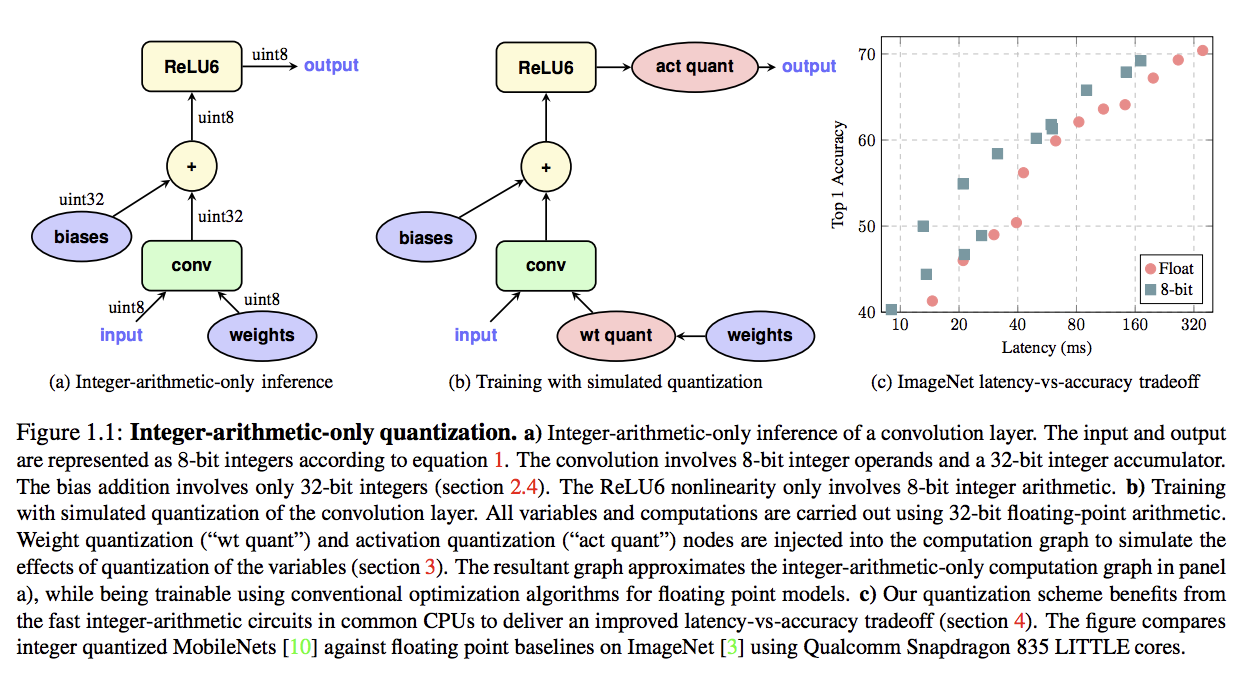
ここでバイアス項が32bitになっていますが、著者らは以下の部分を考慮して32bitにしています。
- バイアスを量子化することに誤差は全体のバイアスに作用してしまう。 量子化により精度が下がってしまう
- バイアスはモデルパラメータのごく一部
しかしバイアスを足した値は$M$もint32であることから32ビットになってしまい、次の活性化関数や層の計算を8bitでは行えないためここで8bitへcast downしています。
Quantized Training Framework
量子化を考慮した学習方法
これまでの量子化方法は学習したモデルのパラメータの値を量子化していました。しかし、これらの方法には2つ欠点があると主張しています。
- 出力チャネルごとの重みの幅に大きな差がでてしまう
- 外れ値に強く影響しやすくなる
なので精度を維持する量子化をするために学習時にQuantized Training Frameworkを利用します。
Quantized Training Frameworkによる学習の流れは以下のとおりです。
- 重み、バイアスをFake QuantizationしてFoward
- 重み、バイアスはfloatを保持してBackpropagation
- 更新した重み、バイアス(float)をFake QuantizationしてFoward
Fake Quantization
Fake QuantizationはfloatのパラメータをFoward時に量子化する手法です。
Fake QuantizationはQuantization Schemeで計算される値を丸める計算を浮動小数点演算で計算しています。
評価
Imagenet Classification, COCO Object Detectionなど様々なタスクで評価しています。
Imagenet
量子化による精度の比較
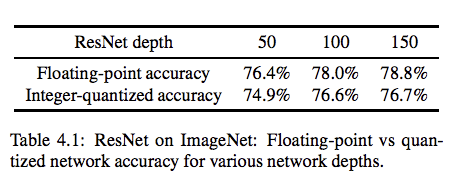
ResNetにおけるFloating pointのモデルと量子化されたモデルの精度比較です。
精度としては2%ほど差があります。
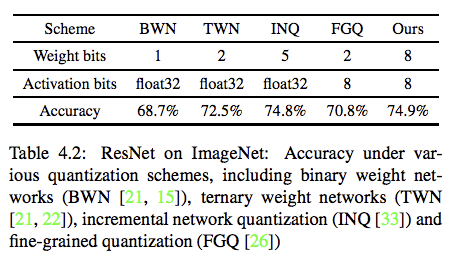
量子化手法の精度比較
先行研究の量子化手法との精度比較です。
本手法が一番高い結果となっています。
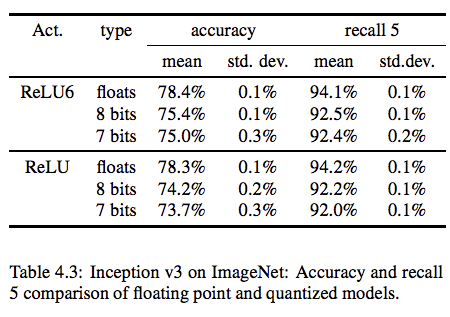
活性化関数の量子化による精度比較
InceptionV3モデルの活性化関数を量子化したことによる精度比較です。
7bitと8bitを比較するとほとんど精度として差がでていない結果となっています。
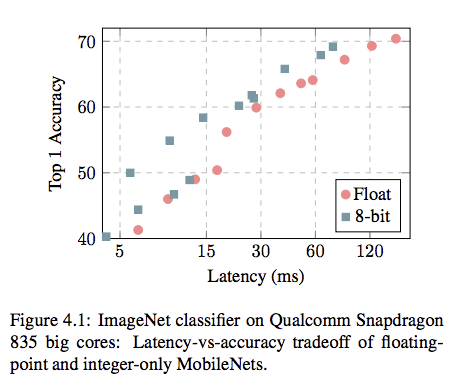
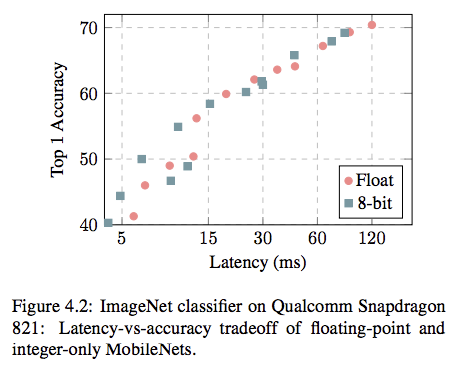
Mobile Netsの量子化
Mobile Netsを量子化したときのLatencyとTop1Accuracyの精度比較です。
Depth Multiplier(DM)を変動させたことによるLatency, Top1Accuracyの結果をマッピングした図です。
Floatと比較するとAccucacy vs Latencyのトレードオフは良くなっている気がします。
またQualcomm Snapdragonはそもそも浮動小数点演算に最適化されているらしく、あまりLatencyに差が出ないということを主張しているので、他のハードだと更に差が出る可能性があります。
Quantization aware training vs after training
Tensorflow技術ブログではQuantization aware trainingと学習した後のモデルに対して量子化を行うQuantization after trainingで精度比較を行っています。
データセットはimagenetです。
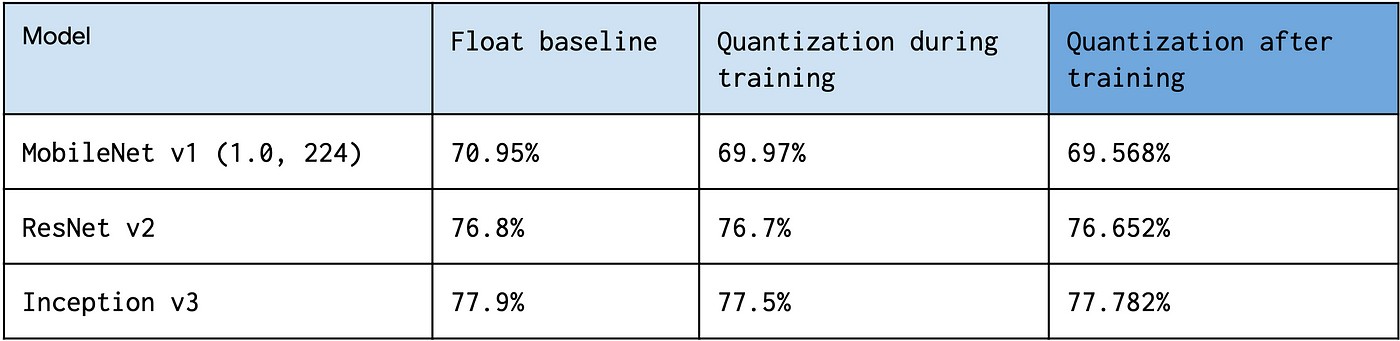
引用:https://miro.medium.com/max/1400/1*jKJdkOme2Z4lFkcG0UEUQg.png
モデルはよりますが、Quantization aware trainigのほうがafter trainingと比べると精度は若干高いことがわかりますがそれほど差が出てないと感じます。また同記事では今後もQuantization aware trainingのAPIは開発していくと主張しており、それまではpost-training quantizationを推奨しています。
参考文献
TensorFlow Model Optimization Toolkit — Post-Training Integer Quantization