アイリスの分類問題でk-近傍法を理解する

k-近傍法とは??

k-近傍法(k-nearest-neighbor)とは､教師あり学習の手法の1つで､k-nearest-neighborという名前からknnと呼ばれる事が多くあります。最も単純な学習アルゴリズムと言われています｡

k近傍法は､ある1つの未知データを､周りのk個のデータから1番多く存在するクラスに分類し､予測します｡わかりやすく図を使って説明していきます｡

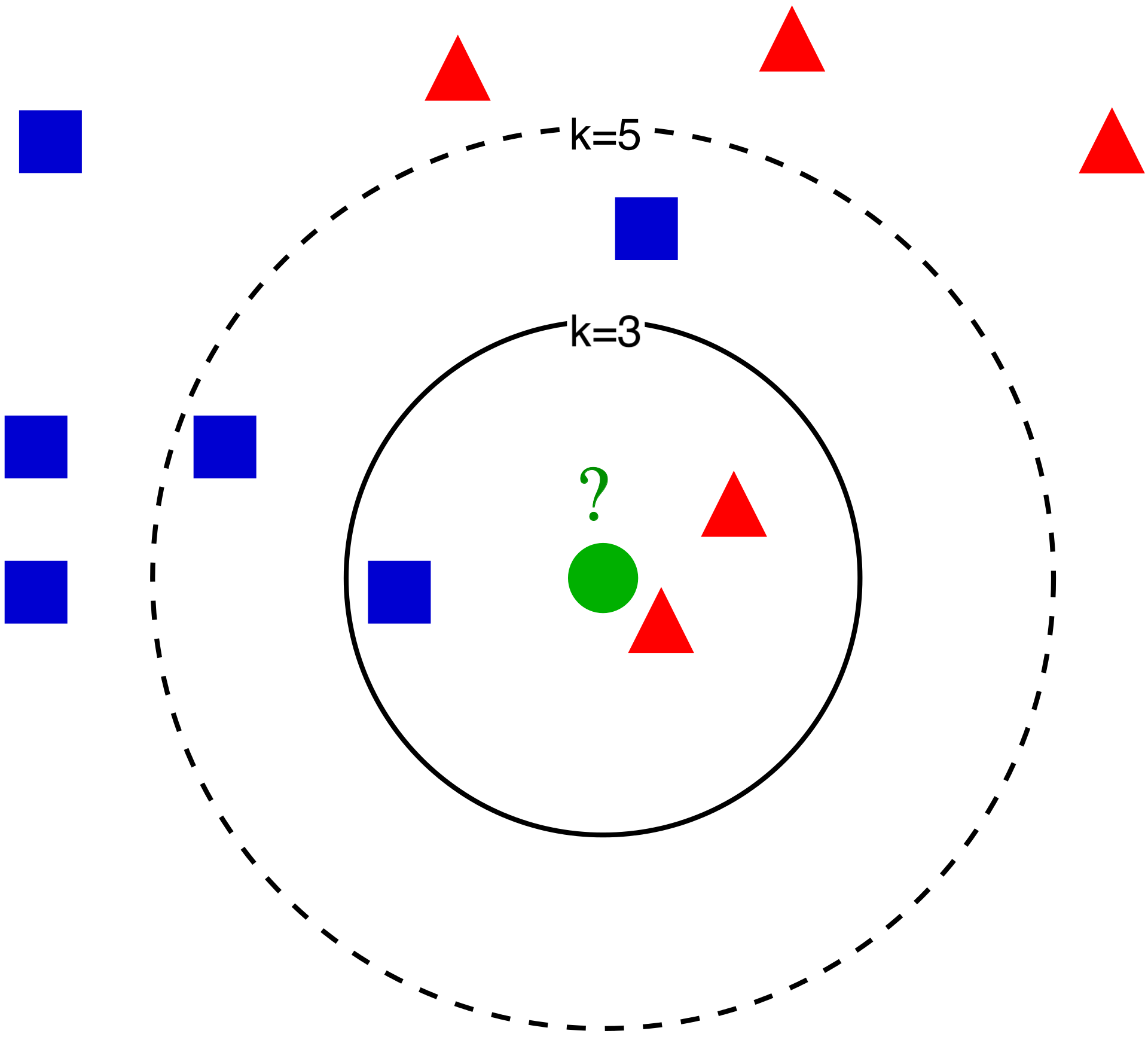
画像(一部編集) : k近傍法 Wikipediaより

今から緑のデータを未知データとして､青と赤のどちらに分類されるか考えます｡

まず､k=3の時､未知データの周りの3つのデータを判断材料とします｡ そうすると､未知データの周りには､青1つと赤2つであるので､多く存在する方である赤に未知データは分類されます｡

次に､k=5の時はどうなるでしょうか? 未知データの周りの5個のデータは､青3個､赤2個であることが分かります｡したがって､k=5の時は､未知データは､青に分類されます｡

もし､k=1であった場合は､未知データの最も近くにあるデータのクラスに分類されることになり､過剰適合に陥りやすいです｡また､k=1の時のk-近傍法は､特別に最近傍法と呼ばれています｡

scikit-learnを使って機械学習モデルを構築していく

scikit-learn （サイキット・ラーン）はPythonのオープンソース機械学習ライブラリで､様々な分類、回帰、クラスタリングアルゴリズムやデータセットが用意されています｡

今回は､scikit-learnに付属されている※アイリスのデータセット(iris_dataset)を使って､k-近傍法を理解していきます｡

※アイリス:アヤメ科アヤメ属の花

必要なライブラリをインポート

%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

簡単に､ライブラリの僕のイメージを説明すると､

• Numpy･･･数値計算を効率的に行うライブラリ
• Pandas･･･表を使って､データを変換,解析するライブラリ
• Matplotlib･･･グラフを描画して可視化するライブラリ

という感じです｡ また %matplotlib inlineを指定すると､Jupyter Notebookで ①グラフがアウトプット行に出力される､②plt.show()を省略してもグラフが出力される､③plt.show()でアウトプット行に２つ以上のグラフ表示可能になります｡

matplotlib inline の謎解明！ |「書けと言われたので書いています」から卒業

アイリスのデータセットをまずは見ていく

今回の目的･ゴール

まず今回の目的は､新しく見つけたアイリスの種類を予測するために､あらかじめ種類の分かっているアイリスのデータを用いて機械学習モデルを構築することです｡

>画像(一部編集) : [アヤメ Wikipediaより](https://ja.wikipedia.org/wiki/%E3%82%A2%E3%83%A4%E3%83%A1#/media/%E3%83%95%E3%82%A1%E3%82%A4%E3%83%AB:Iris_sanguinea_01.JPG)

上の画像が､アイリスです｡この花のサンプルデータから新しく見つけたアイリスの種類を分類するモデルを作るという問題です｡

irisデータセット読み込み

まず､サンプルのアイリスデータセットを読み込んでいきます｡サンプルのアイリスデータは､scikit-learnのdatasetsモジュールに含まれていて､load_iris関数で読み込むことができます｡

from sklearn.datasets import load_iris 
iris_dataset = load_iris() 

アイリスのインスタンスiris_datasetを生成しました｡

ではこのデータセットの中身を見ていきます｡

print(iris_dataset.data)
print(iris_dataset.data.shape)

これを実行すると
ーーーーーーーーーーー
[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
･･･････
[6.2 3.4 5.4 2.3]
[5.9 3. 5.1 1.8]]

(150, 4)
ーーーーーーーーーーー
みたいな感じで150×4のデータが表示される事がわかります｡

print(iris_dataset.target)
print(iris_dataset.target_names)

また､↑を実行すると､
ーーーーーーーーーーー
[0 0 0 0 0 0 0 ･･･ 1 1 1 1 ･･･ 2 2 2]
['setosa' 'versicolor' 'virginica']
ーーーーーーーーーーー
『setosa(=0)』,『versicolor(=1)』,『virginica(=2)』の3種類のクラスに分類されている事がわかります｡

Pandasでデータを分かりやすくする

まだ､配列でデータを確認しただけなので､irisデータセットについてよく理解できていません｡ そこで､Pandasライブラリで表を作ることで分かりやすくしていきます｡

DataFrameを作る

上で出力したデータを表にするには､配列をDataFrameというデータ構造に落とし込む必要があります｡ そこで､

1. がく片､花弁の長さ､幅の関係を示す表(説明変数)
2. アイリスの種類を示す表(目的変数)
3. 1と2を足し合わせた表

の3つを作成していきます｡

1. がく片､花弁の長さ､幅の関係を示す表(説明変数)

1.py

iris_data_ = {
    'がく片の長さ': iris_dataset.data[:,0],    
    'がく片の幅': iris_dataset.data[:,1], 
    '花弁の長さ': iris_dataset.data[:,2],
    '花弁の幅': iris_dataset.data[:,3]
}
iris_data = pd.DataFrame(iris_data_)
display(iris_data)

2. アイリスの種類を示す表(目的変数)

2.py

iris_target_ = {
    'アイリスの種類': iris_dataset.target    
}
iris_target = pd.DataFrame(iris_target_)
display(iris_target)

3. 1と2を足し合わせた表

3.py

iris_all = pd.concat([iris_data,iris_target], axis=1)
display(iris_all)

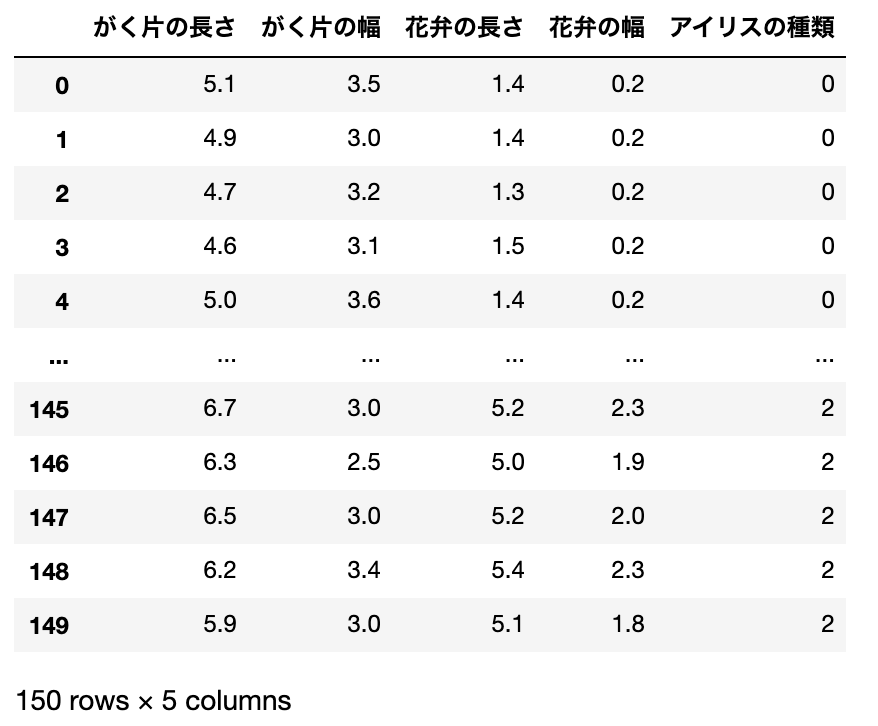
concatメソッドは､複数のDataFrameを列方向あるいは行方向に結合するメソッドで､iris_dataとiris_targetを列方向(axis=1)に結合することを指定しています｡

訓練データとテストデータに分割

なぜ訓練データとテストデータに分割するのか?

今回は､新たに見つけたアイリスが3種類の『setosa』,『versicolor』,『virginica』のどれに分類されるかを予測する機械学習モデルを構築しています｡そこで､構築したモデルがどれほど信頼性のあるモデルなのかを知っておく必要があります｡

しかし､モデルの構築に使ったデータを､モデルの評価に使うことはできません｡
(モデルの構築に使ったデータをもとに､精度を出してしまうと､カンニングしたテストで100点とった人を､成績優秀者と判断するのと一緒になってしまいます｡)

そこで訓練データとテストデータに分けて､訓練データを使ってモデルを作成して､テストデータで予測がどれくらい的中したのか答え合わせをして､モデルの精度を確かめます｡

またテストデータは､表の150行のどこかでキレイに分割してしまうと､データが偏ってしまうので(ex.101行目以降は､アイリスの種類は『virginica』しかない)､150行のデータをランダムにして､訓練データとテストデータに分割したいところです｡

そこで､train_test_split関数を使います｡

train_test_split関数で分割

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(iris_data, iris_target)

↑のコードで分割していきます｡

1行目は､train_test_split関数を使うためのインポート文です｡

2行目で実際に､訓練データとテストデータに分割しています｡ここで､test_train_split関数の引数にrandom_state=○○と渡すと乱数シードが固定されて常に同じように分割されます｡また､test_size=□□やtrain_size=△△と引数で渡すとデータ全体のテストデータ､訓練データの割合､個数を指定する事ができます｡デフォルトは､test_size=0.25で25%がテスト用、残りの75%が訓練用となります｡

今回はデフォルトのままで行きます｡

説明変数の訓練データ

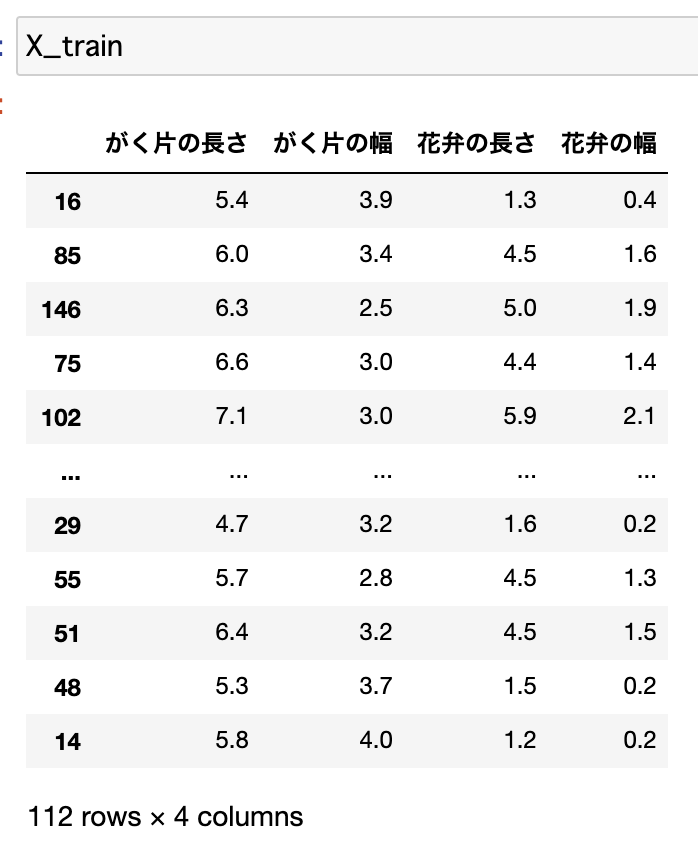
目的変数の訓練データ

しっかり分割されているか中身を確認すると､要素数も112(≒150×0.75)､38(≒150×0.25)となっており､しっかり分割されている事がわかります｡テストデータも同様に確認することができます｡

機械学習モデルを構築する

今回はタイトルにもある通り､k-近傍法を使っていきます｡k-近傍法は訓練データを格納するだけで良いので､単純な流れでモデルを構築する事ができます｡

モデル構築

from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(X_train,y_train.values.ravel())

上を実行します｡

今回は､近傍点の数を1にします｡冒頭でも説明しましたように､n_neighborsの値を変えると､予測結果やモデルの精度は変わってきます｡

3行目のfitメソッドで訓練データを学習します｡第2引数のvalues.ravel()の部分は､ravel関数で多次元リストを1次元のリストにして返しています｡次元数をあわせることで､fitメソッドを使えるようにします｡あまりきれいな書き方ではないです｡

アイリスの種類を予測させる

ここでは､新しく2つのアイリスの種類を予測させるというケースにします｡

1つ目のアイリスX_new1は､がく片の長さ4.2cm､がく片の幅2.5cm､花弁の長さ4.0cm､花弁の幅1.0cmであり､2つ目のアイリスX_new2は､がく片の長さ7.0cm､がく片の幅2.5cm､花弁の長さ7.8cm､花弁の幅2.2cmであったとします｡

X_new1 = np.array([[4.2, 2.5, 4.0, 1.0]])
X_new2 = np.array([[7.0, 2.5, 7.8, 2.2]])

次に､この2つのアイリスが3種類のうちのどれか予測させます｡

prediction1 = knn.predict(X_new1)
prediction2 = knn.predict(X_new2)

print("X_new1の予測 : {}".format(iris_dataset['target_names'][prediction1]))
print("X_new2の予測 : {}".format(iris_dataset['target_names'][prediction2]))

出力は､､､
ーーーーーーーーーーーーーーーーーー
X_new1の予測 : ['versicolor']
X_new2の予測 : ['virginica']
ーーーーーーーーーーーーーーーーーー
ということで､1つ目のアイリスがversicolor､2つ目のアイリスがvirginicaであると判断したことが分かります｡ まだまだ安心できないので､次にこの予測がどのぐらいの確率で当たるのか､見ていきます｡

モデルの評価

先程作っておいた､もうすでにアイリスの種類が分かっているテストデータ(まだモデル構築に使っていない残りの25%)を予測させて､実際と予測がどれだけマッチしているか調べます｡

y_pred = knn.predict(X_test)
print("モデルの精度 : {:.2f}".format(np.mean(y_pred == y_test.values.ravel())))

ーーーーーーーーーーーーーーーーーー
モデルの精度 : 0.97
ーーーーーーーーーーーーーーーーーー
したがって､このモデルのテストデータに対する精度が0.97であることが分かりました｡
100本中97本のアイリスの種類を当てる事ができるので､十分信頼できると分かります｡

まとめ

最後まで見て頂きありがとうございました｡

すでにアイリスの分類問題に関する情報もk-近傍法に関する情報もネット上に溢れかえっていますが､まだ､機械学習の勉強を始めたばかりだったので､1ヶ月前の自分に読ませるつもりで書きました｡

間違っているところがありましたら､コメントしていただけると嬉しいです｡