Swiftで四元数（クォータニオン）の回転までやってみた

雰囲気でエンジニアやっているものです。

ネタがなさすぎるのでやってみました。特に使いみちはありません。
大学のとき数学科で四元数と八元数の研究していたので、10年以上前の記憶を掘り起こしながらやってみました。
そういえば数学も雰囲気でやってました。

まずは復習がてら複素数から

複素数は結構やられている方も多いのでラフに行きます。

struct Complex {
    let x: Double
    let y: Double
    
    init(x: Double, y: Double) {
        self.x = x
        self.y = y
    }
    
    // 極形式
    init(r: Double, theta: Double) {
        self.x = r * cos(theta)
        self.y = r * sin(theta)
    }
}

func == (a: Complex, b: Complex) -> Bool {
    return (a.x == b.x) && (a.y == b.y)
}

// 足し算の定義
func + (z: Complex, w: Complex) -> Complex {
    return Complex(x: z.x + w.x, y: z.y + w.y)
}

// -の定義
prefix func - (z: Complex) -> Complex {
    return Complex(x: -z.x, y: -z.y)
}

// 引き算
func - (z: Complex, w: Complex) -> Complex {
    return Complex(x: z.x - w.x, y: z.y - w.y)
}

// 定数倍
func * (a: Double, z: Complex) -> Complex {
    return Complex(x: a * z.x, y: a * z.y)
}

// 複素数同士の掛け算
func * (z: Complex, w: Complex) -> Complex {
    return Complex(x: z.x * w.x - z.y * w.y, y: z.x * w.y + z.y * w.x)
}

// 複素数同士の割り算
func / (z: Complex, w: Complex) -> Complex {
    let wInv = Complex(x: w.x / (w.x * w.x + w.y * w.y), y: -w.y / (w.x * w.x + w.y * w.y))
    return z * wInv
}

// ノルム
func abs(z: Complex) -> Double {
    return sqrt(z.x * z.x + z.y * z.y)
}

// 偏角
func arg(z: Complex) -> Double {
    let r = abs(z: z)
    if r == 0 {
        return 0
    }
    let t = acos(z.x / r)
    return (z.y >= 0) ? t : 2 * .pi - t
}

// 虚数iの定義
let i = Complex(x: 0, y: 1)

確認します

いちばん大事な $ i^2 = -1 $ が満たされているかですね。

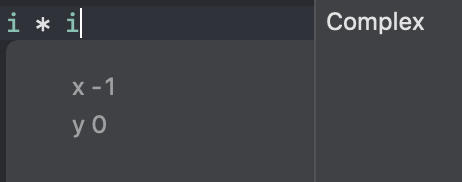
おお、できました。虚数という現実にないものを目で見れるって不思議。

回転してみます。
$ x + iy $ を$r$倍して $\theta$ 回転させるということは $ (x + iy)(r(\cos\theta + i\sin\theta)) $ 、つまりただの掛け算ですね。

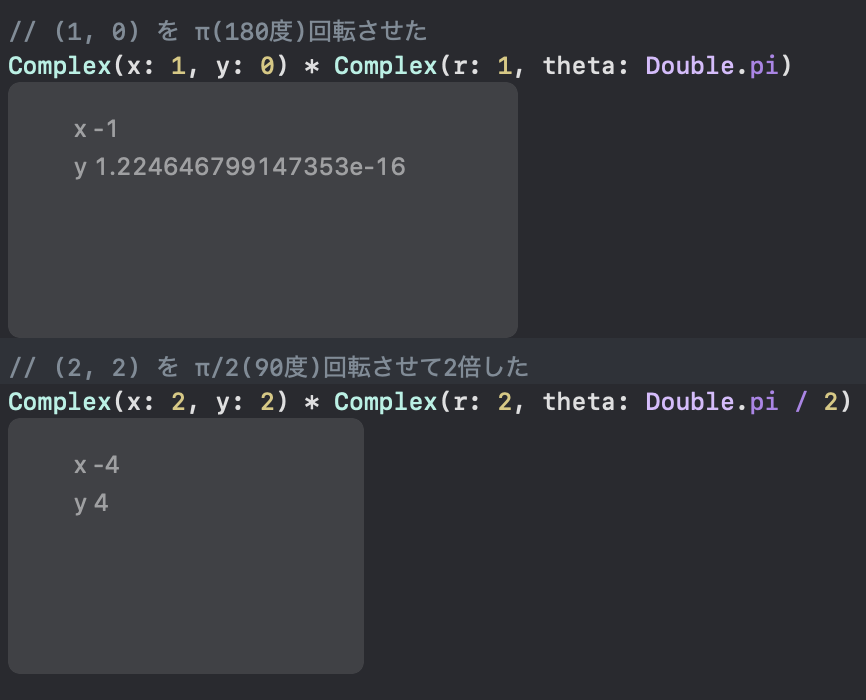
うん、まぁよさそうですね。

四元数（クォータニオン）

四元数の細かい説明は抜かします。

$$ i^2 = j^2 = k^2 = ijk = -1 \quad ij = k \quad jk = i \quad ki = j \quad ji = -k \quad kj = -i \quad ki = -j $$

を満たせばいい感じかな。

// 四元数を表すStruct
struct Quaternion {
    let x: Double
    let y: Double
    let z: Double
    let t: Double // 実部
}

// 四元数 ai + bj + ck + d は以下で表す
Quaternion(x: a, y: b, z: c, t: d)

こいつに複素数のときと同様、四則演算を定義していきます（使わなさそうなやつはとりあえず省略した）

struct Quaternion {
    let x: Double
    let y: Double
    let z: Double
    let t: Double // 実部
}

func + (r: Quaternion, q: Quaternion) -> Quaternion {
    return Quaternion(x: r.x + q.z, y: r.y + q.y, z: r.z + q.z, t: r.t + q.t)
}

prefix func - (r: Quaternion) -> Quaternion {
    return Quaternion(x: -r.x, y: -r.y, z: -r.z, t: -r.t)
}

func - (r: Quaternion, q: Quaternion) -> Quaternion {
    return Quaternion(x: r.x - q.x, y: r.y - q.y, z: r.z - q.z, t: r.t - q.t)
}

func * (a: Double, r: Quaternion) -> Quaternion {
    return Quaternion(x: a * r.x, y: a * r.y, z: a * r.z, t: a * r.t)
}

func * (r: Quaternion, q: Quaternion) -> Quaternion {
    return Quaternion(
        x: r.t * q.x + r.x * q.t + r.y * q.z - r.z * q.y,
        y: r.t * q.y - r.x * q.z + r.y * q.t + r.z * q.x,
        z: r.t * q.z + r.x * q.y - r.y * q.x + r.z * q.t,
        t: r.t * q.t - r.x * q.x - r.y * q.y - r.z * q.z
    )
}

let i = Quaternion(x: 1, y: 0, z: 0, t: 0)
let j = Quaternion(x: 0, y: 1, z: 0, t: 0)
let k = Quaternion(x: 0, y: 0, z: 1, t: 0)

掛け算が地獄ですねー紙とペンでやるのが至高です。

最初の条件満たすかチェック

おお、間違えてなかったようです(Equatableで == の定義して比較したほうがわかりやすかったですね)

回転してみる

回転はちょっと面倒ですが、 $ r = (r_0, r_1, r_2) \quad |r| = 1 $ を回転軸にして $\theta$ 回転するときの回転を表す四元数は

$$ \cos\frac{\theta}{2} + ir_0\sin\frac{\theta}{2} + jr_1\sin\frac{\theta}{2} + kr_2\sin\frac{\theta}{2} $$

と表せます。

四元数 $p$ 、回転を表す四元数を $q$ とすると回転した後の四元数は

$$ qpq^* $$

となります。
ここで $ q^* $ は共軛四元数で、虚部の符号を反転したものです。

$$ q = ai + bj + ck + d \quad q^* = -ai - bj -ck + d $$

なので回転を表す四元数と共軛を作ってあげます

struct Quaternion: Equatable {
    let x: Double
    let y: Double
    let z: Double
    let t: Double
    
    init(x: Double, y: Double, z: Double, t: Double) {
        self.x = x
        self.y = y
        self.z = z
        self.t = t
    }
    
    // 回転を表す四元数
    init(r: (Double, Double, Double), theta: Double) {
        let norm = sqrt(r.0 * r.0 + r.1 * r.1 + r.2 * r.2)
        let unitVector = (r.0 / norm, r.1 / norm, r.2 / norm)
        self.x = unitVector.0 * sin(theta / 2)
        self.y = unitVector.1 * sin(theta / 2)
        self.z = unitVector.2 * sin(theta / 2)
        self.t = cos(theta / 2)
    }

    // 共軛
    func conjugate() -> Quaternion {
        return Quaternion(x: -self.x, y: -self.y, z: -self.z, t: self.t)
    }
}

んでは回転します。

おー回ってますね。
実部も0に近くなってて、座標に変換できるようになってますね。

おわり

なんの役にも立たないことをしてみました。
やはり数学は紙とペンが至高ですね（2回目）
八元数（オクトニオン）までやってみようかと思ったけど、流石に面倒くさくてやめました。