マールス(ラテン語:Mārs) は、ローマ神話における戦と農耕の神[1]。日本語では「マルス」や「マーズ」と呼ばれる[1]。英語読みは「マーズ」(Mars)である。
元の名はマーウォルス(マウォルス、Māvors)であるらしく、また、マーメルス(マメルス、Māmers)とも呼ばれていた[1]。
ギリシア神話のアレースと同一視され、軍神としてグラディーウゥス(グラディウス、Gradīvus、「進軍する者」の意)という異称でも呼ばれる[1]。しかし、疫病神のように思われて全く良い神話のないアレースに対し、マールスは勇敢な戦士、青年の理想像として慕われ、主神並みに篤く崇拝された重要な神である[1]。聖獣は狼、聖鳥はキツツキである[1]。
マールスは他のローマ神話のどの神とも違い、ローマ建国時に既にローマにいた神であった。3月の神であるのも、気候がよくなり軍隊を動かす季節と一致する。また、これが農耕の始まる季節に一致している[1]。当時のローマ暦は、新年は農耕の始まる3月におかれた。主神と同様に扱われたために、ローマ建設者とされる初代ロームルス王の父親という伝承まで残されている[1]。
旧来の学説では、ローマ人が農耕民族であったため、マールスも元々は農耕神で、勇敢に戦い領地を増やしたロームルス王と像が重なり、後に軍神としても祭られるようになったと考えられていた[1]。また、元は地下神であったため、地下に眠る死者との関連づけから軍神モートになったとする説もあった。しかし現在では、インド・ヨーロッパ語族比較神話学の進歩により、マールスは本来軍神であり、三機能イデオロギーの第二機能(戦闘)を担っていたと考えられている。しかし、マールスの名前はインド・ヨーロッパ語族とは関係のないエトルリア人に崇拝された神マリスを原型としている。
マールスからは「マルクス」「マルケッルス」「マリウス」「マルティヌス」といったローマ人名が派生し、それらをヨーロッパ各語にアレンジした人名が使われている。
また、マールスは、男性の武勇や闘争心を表す比喩として用いられたり、軍神の代名詞として用いられることも多い。ウェヌス(ヴィーナス)が「愛」「女性」を象徴するのに対して、マールスは「武勇」「男性」「火星」の象徴として用いられることも多い。性別記号で男性は「♂」と表記されるが、本来はマールスを意味する記号である。
System F 多相ラムダ計算の型推論は決定不能なので型は必ず書かなくてはなりません。
えーと、型抽象とかあって型適用することで多相的な型システムが構築できるので全称型∀や存在型∃、型適用があります。
23章
図23-1.多相ラムダ計算(System F)
→ ∀ λ→(図9-1)の拡張
構文
t ::= … 項:
λX.t 型抽象
t[T] 型適用
v ::= … 値:
λX.t 型抽象値
T ::= … 型:
X 型変数
∀X.T 全称型
Γ::= … 文脈:
Γ,X 型変数の束縛
評価 t ==> t’
t1 ==> t1’
————————————————(E-TApp)
t1[T2] ==> t1’[T2]
(λX.t12)[T2] ==> [X -> T2] t12 (E-TAppTAbs)
型付け Γ ⊢ t : T
Γ,X ⊢ t2 : T2
—————————————— (T-TAbs)
Γ ⊢ λX.t2 : ∀X.T2
Γ ⊢ t1 : ∀X.T12
—————————————— (T-TApp)
Γ ⊢ t1[T2] : [X -> T2] T12
図24-1. 存在型
新しい構文形式
t ::= ... 項:
{*T,t} as T パッケージ化
let {X,x}=t in t アンパッケージ化
v ::= ... 値:
{*T,v} as T パッケージの値
T ::= ... 型:
{∃ X,T} 存在型
新しい評価規則 t ==> t'
let {X,x} = ({*T11,v12}as T1) in t2
------------------------ (E-UnpackPack)
==> [X->T11][x->v12]t2
t12 ==> t12'
------------------------ (E-Pack)
{*T11,t12} as T1
==> {*T11,t12'} as T1
t1 ==> t1'
----------------------- (E-Unpack)
let {X,x}=t1 in t2
==> let {X,x}=t1' in t2
新しい型付け規則 Γ |- t : T
Γ |- t2 : [X -> U] T2
--------------------------------------- (T-Pack)
Γ |- {*U, t2} as {∃ X, T2} : {∃ X, T2}
Γ |- t1 : {∃ X, T12}
Γ,X,x:T12 |- t2 : T2
-------------------------------- (T-Unpack)
Γ |- let {X,x}=t1 in t2 : T2
実装
- fullpoly フル全称型、存在型 bool+nat+unit+float+string+λ+let+letrec+fix+inert+as+record+all+some(23,24章)
fullpoly.pl
プログラムの全体を見る
:- discontiguous((/-)/2).
:- op(1200, xfx, ['--', :-]).
:- op(1100, xfy, [in]).
:- op(1050, xfy, ['=>']).
:- op(920, xfx, [==>, ==>>]).
:- op(910, xfx, [/-]).
:- op(600, xfy, [::, as]).
:- op(500, yfx, [$, !, tsubst, tsubst2, subst, subst2, tmsubst, tmsubst2]).
:- op(400, yfx, [#]).
:- style_check(- singleton).
% ------------------------ SYNTAX ------------------------
:- use_module(rtg).
w ::= bool | nat | unit | float | string | true | false. % キーワード:
syntax(x). x(X) :- \+ w(X), atom(X), sub_atom(X, 0, 1, _, P), (char_type(P, lower) ; P = '_'). % 識別子:
syntax(tx). tx(TX) :- atom(TX), sub_atom(TX, 0, 1, _, P), char_type(P, upper). % 型変数:
syntax(floatl). floatl(F) :- float(F). % 浮動小数点数
syntax(stringl). stringl(F) :- string(F). % 文字列
syntax(l). l(L) :- atom(L) ; integer(L). % ラベル
list(A) ::= [] | [A | list(A)]. % リスト
t ::= % 型:
bool % ブール値型
| nat % 自然数型
| unit % Unit型
| float % 浮動小数点数型
| string % 文字列型
| tx % 型変数
| (t -> t) % 関数の型
| {list(l : t)} % レコードの型
| {some(tx), t} % 存在型
| (all(tx) => t) % 全称型
.
m ::= % 項:
true % 真
| false % 偽
| if(m, m, m) % 条件式
| 0 % ゼロ
| succ(m) % 後者値
| pred(m) % 前者値
| iszero(m) % ゼロ判定
| unit % 定数unit
| floatl % 浮動小数点数値
| m * m % 浮動小数点乗算
| stringl % 文字列定数
| x % 変数
| (fn(x : t) -> m) % ラムダ抽象
| m $ m % 関数適用
| (let(x) = m in m) % let束縛
| fix(m) % mの不動点
| inert(t)
| m as t % 型指定
| {list(l = m)} % レコード
| m # l % 射影
| m as t % 型指定
| {(t, m)} as t % パッケージ化
| (let(tx, x) = m in m) % アンパッケージ化
| (fn(tx) => m) | m![t] % 型適用
.
n ::= % 数値:
0 % ゼロ
| succ(n) % 後者値
.
v ::= % 値:
true % 真
| false % 偽
| n % 数値
| unit % 定数unit
| floatl % 浮動小数点数値
| stringl % 文字列定数
| (fn(x : t) -> m) % ラムダ抽象
| {list(l = v)} % レコード
| {(t, v)} as t % パッケージ化
| (fn(tx) => m)
.
% ------------------------ SUBSTITUTION ------------------------
bool![(J -> S)] tsubst bool.
nat![(J -> S)] tsubst nat.
unit![(J -> S)] tsubst unit.
float![(J -> S)] tsubst float.
string![(J -> S)] tsubst string.
J![(J -> S)] tsubst S :- tx(J).
X![(J -> S)] tsubst X :- tx(X).
(T1 -> T2)![(J -> S)] tsubst (T1_ -> T2_) :- T1![(J -> S)] tsubst T1_, T2![(J -> S)] tsubst T2_.
{Mf}![(J -> S)] tsubst {Mf_} :- maplist([L : T, L : T_] >> (T![(J -> S)] tsubst T_), Mf, Mf_).
{some(TX), T2}![(J -> S)] tsubst {some(TX), T2_} :- T2![TX, (J -> S)] tsubst2 T2_.
(all(TX) => T2)![(J -> S)] tsubst (all(TX) => T2_) :- T2![TX, (J -> S)] tsubst2 T2_.
T![X, (X -> S)] tsubst2 T.
T![X, (J -> S)] tsubst2 T_ :- T![(J -> S)] tsubst T_.
true![(J -> M)] subst true.
false![(J -> M)] subst false.
if(M1, M2, M3)![(J -> M)] subst if(M1_, M2_, M3_) :- M1![(J -> M)] subst M1_, M2![(J -> M)] subst M2_,
M3![(J -> M)] subst M3_.
0![(J -> M)] subst 0.
succ(M1)![(J -> M)] subst succ(M1_) :- M1![(J -> M)] subst M1_.
pred(M1)![(J -> M)] subst pred(M1_) :- M1![(J -> M)] subst M1_.
iszero(M1)![(J -> M)] subst iszero(M1_) :- M1![(J -> M)] subst M1_.
unit![(J -> M)] subst unit.
F1![(J -> M)] subst F1 :- float(F1).
M1 * M2![(J -> M)] subst M1_ * M2_ :- M1![(J -> M)] subst M1_, M2![(J -> M)] subst M2_.
X![(J -> M)] subst X :- string(X).
J![(J -> M)] subst M :- x(J).
X![(J -> M)] subst X :- x(X).
(fn(X : T1) -> M2)![(J -> M)] subst (fn(X : T1) -> M2_) :- M2![X, (J -> M)] subst2 M2_.
M1 $ M2![(J -> M)] subst (M1_ $ M2_) :- M1![(J -> M)] subst M1_, M2![(J -> M)] subst M2_.
(let(X) = M1 in M2)![(J -> M)] subst (let(X) = M1_ in M2_) :- M1![(J -> M)] subst M1_, M2![X, (J -> M)] subst2 M2_.
fix(M1)![(J -> M)] subst fix(M1_) :- M1![(J -> M)] subst M1_.
inert(T1)![(J -> M)] subst inert(T1).
(M1 as T1)![(J -> M)] subst (M1_ as T1) :- M1![(J -> M)] subst M1_.
{Mf}![(J -> M)] subst {Mf_} :- maplist([L = Mi, L = Mi_] >> (Mi![(J -> M)] subst Mi_), Mf, Mf_).
M1 # L![(J -> M)] subst M1_ # L :- M1![(J -> M)] subst M1_.
({(T1, M2)} as T3)![(J -> M)] subst ({(T1, M2_)} as T3) :- M2![(J -> M)] subst M2_.
(let(TX, X) = M1 in M2)![(J -> M)] subst (let(TX, X) = M1_ in M2_)
:- M1![X, (J -> M)] subst2 M1_, M2![X, (J -> M)] subst2 M2_.
(fn(TX) => M2)![(J -> M)] subst (fn(TX) => M2_) :- M2![(J -> M)] subst M2_.
M1![T2]![(J -> M)] subst (M1_![T2]) :- M1![(J -> M)] subst M1_.
S![(J -> M)] subst _ :- writeln(error : subst(J, M, S)), fail.
S![J, (J -> M)] subst2 S.
S![X, (J -> M)] subst2 M_ :- S![(J -> M)] subst M_.
true![(J -> S)] tmsubst true.
false![(J -> S)] tmsubst false.
if(M1, M2, M3)![(J -> S)] tmsubst if(M1_, M2_, M3_) :- M1![(J -> S)] tmsubst M1_, M2![(J -> S)] tmsubst M2_,
M3![(J -> S)] tmsubst M3_.
0![(J -> S)] tmsubst 0.
succ(M1)![(J -> S)] tmsubst succ(M1_) :- M1![(J -> S)] tmsubst M1_.
pred(M1)![(J -> S)] tmsubst pred(M1_) :- M1![(J -> S)] tmsubst M1_.
iszero(M1)![(J -> S)] tmsubst iszero(M1_) :- M1![(J -> S)] tmsubst M1_.
unit![(J -> M)] tmsubst unit.
F1![(J -> M)] tmsubst F1 :- float(F1).
M1 * M2![(J -> M)] tmsubst M1_ * M2_ :- M1![(J -> M)] tmsubst M1_, M2![(J -> M)] tmsubst M2_.
X![(J -> M)] tmsubst X :- string(X).
X![(J -> S)] tmsubst X :- x(X).
(fn(X : T1) -> M2)![(J -> S)] tmsubst (fn(X : T1_) -> M2_) :- T1![(J -> S)] tsubst T1_, M2![(J -> S)] tmsubst M2_.
M1 $ M2![(J -> S)] tmsubst (M1_ $ M2_) :- M1![(J -> S)] tmsubst M1_, M2![(J -> S)] tmsubst M2_.
(let(X) = M1 in M2)![(J -> S)] tmsubst (let(X) = M1_ in M2_) :- M1![(J -> S)] tmsubst M1_, M2![(J -> S)] tmsubst M2_.
fix(M1)![(J -> M)] tmsubst fix(M1_) :- M1![(J -> M)] tmsubst M1_.
inert(T1)![(J -> M)] tmsubst inert(T1).
(M1 as T1)![(J -> S)] tmsubst (M1_ as T1_) :- M1![(J -> S)] tmsubst M1_, T1![(J -> S)] tsubst T1_.
{Mf}![(J -> M)] tmsubst {Mf_} :- maplist([L = Mi, L = Mi_] >> (Mi![(J -> M)] tmsubst Mi_), Mf, Mf_).
M1 # L![(J -> M)] tmsubst M1_ # L :- M1![(J -> M)] tmsubst M1_.
({(T1, M2)} as T3)![(J -> M)] tmsubst ({(T1_, M2_)} as T3_) :- T1![(J -> S)] tsubst T1_, M2![(J -> M)] tmsubst M2_, T3![(J -> S)] tsubst T3_.
(let(TX, X) = M1 in M2)![(J -> M)] tmsubst (let(TX, X) = M1_ in M2_)
:- M1![TX, (J -> M)] tmsubst2 M1_, M2![TX, (J -> M)] tmsubst2 M2_.
(fn(TX) => M2)![(J -> S)] tmsubst (fn(TX) => M2_) :- M2![TX, (J -> S)] tmsubst2 M2_.
M1![T2]![(J -> S)] tmsubst (M1_![T2_]) :- M1![(J -> S)] tmsubst M1_, T2![(J -> S)] tsubst T2_.
T![X, (X -> S)] tmsubst2 T.
T![X, (J -> S)] tmsubst2 T_ :- T![(J -> S)] tmsubst T_.
gett(Γ, X, T) :- member(X:T, Γ).
gett(Γ, X, T) :- member(X:T=_, Γ).
% ------------------------ EVALUATION ------------------------
e([L = M | Mf], M, [L = M_ | Mf], M_) :- \+ v(M).
e([L = M | Mf], M1, [L = M | Mf_], M_) :- v(M), e(Mf, M1, Mf_, M_).
Γ /- if(true, M2, _) ==> M2.
Γ /- if(false, _, M3) ==> M3.
Γ /- if(M1, M2, M3) ==> if(M1_, M2, M3) :- Γ /- M1 ==> M1_.
Γ /- succ(M1) ==> succ(M1_) :- Γ /- M1 ==> M1_.
Γ /- pred(0) ==> 0.
Γ /- pred(succ(N1)) ==> N1 :- n(N1).
Γ /- pred(M1) ==> pred(M1_) :- Γ /- M1 ==> M1_.
Γ /- iszero(0) ==> true.
Γ /- iszero(succ(N1)) ==> false :- n(N1).
Γ /- iszero(M1) ==> iszero(M1_) :- Γ /- M1 ==> M1_.
Γ /- F1 * F2 ==> F3 :- float(F1), float(F2), F3 is F1 * F2.
Γ /- V1 * M2 ==> V1 * M2_ :- v(V1), Γ /- M2 ==> M2_.
Γ /- M1 * M2 ==> M1_ * M2 :- Γ /- M1 ==> M1_.
Γ /- X ==> M :- x(X), member(X:_=M, Γ).
Γ /- (fn(X : _) -> M12) $ V2 ==> R :- v(V2), M12![(X -> V2)] subst R.
Γ /- V1 $ M2 ==> V1 $ M2_ :- v(V1), Γ /- M2 ==> M2_.
Γ /- M1 $ M2 ==> M1_ $ M2 :- Γ /- M1 ==> M1_.
Γ /- (let(X) = V1 in M2) ==> M2_ :- v(V1), M2![(X -> V1)] subst M2_.
Γ /- (let(X) = M1 in M2) ==> (let(X) = M1_ in M2) :- Γ /- M1 ==> M1_.
Γ /- fix((fn(X : T) -> M12)) ==> M12_ :- M12![(X -> fix((fn(X : T) -> M12)))] subst M12_.
Γ /- fix(M1) ==> fix(M1_) :- Γ /- M1 ==> M1_.
Γ /- V1 as _ ==> V1 :- v(V1).
Γ /- M1 as T ==> M1_ as T :- Γ /- M1 ==> M1_.
Γ /- {Mf} ==> {Mf_} :- e(Mf, M, Mf_, M_), Γ /- M ==> M_.
Γ /- {Mf} # L ==> M :- member(L = M, Mf).
Γ /- M1 # L ==> M1_ # L :- Γ /- M1 ==> M1_.
Γ /- {(T1, M2)} as T3 ==> {(T1, M2_)} as T3 :- Γ /- M2 ==> M2_.
Γ /- (let(_, X) = {(T11, V12)} as _ in M2) ==> M :- v(V12), M2![(X -> V12)] subst M2_,
M2_![(X -> T11)] tmsubst M.
Γ /- (let(TX, X) = M1 in M2) ==> (let(TX, X) = M1_ in M2)
:- Γ /- M1 ==> M1_.
Γ /- (fn(X) => M11)![T2] ==> M11_ :- M11![(X -> T2)] tmsubst M11_.
Γ /- M1![T2] ==> M1_![T2] :- Γ /- M1 ==> M1_.
Γ /- M ==>> M_ :- Γ /- M ==> M1, Γ /- M1 ==>> M_.
Γ /- M ==>> M.
gettabb(Γ, X, T) :- member(X :: T, Γ).
compute(Γ, X, T) :- tx(X), gettabb(Γ, X, T).
simplify(Γ, T, T_) :- compute(Γ, T, T1), simplify(Γ, T1, T_).
simplify(Γ, T, T).
Γ /- S = T :- simplify(Γ, S, S_), simplify(Γ, T, T_), Γ /- S_ == T_.
Γ /- bool == bool.
Γ /- nat == nat.
Γ /- unit == unit.
Γ /- float == float.
Γ /- string == string.
Γ /- X == T :- tx(X), gettabb(Γ, X, S), Γ /- S = T.
Γ /- S == X :- tx(X), gettabb(Γ, X, T), Γ /- S = T.
Γ /- X == X :- tx(X).
Γ /- (S1 -> S2) == (T1 -> T2) :- Γ /- S1 = T1, Γ /- S2 = T2.
Γ /- {Sf} == {Tf} :- length(Sf, Len), length(Tf, Len),
maplist([L : T] >> (member(L : S, Sf), Γ /- S = T), Tf).
Γ /- (all(TX1) => S2) == (all(_) => T2) :- [TX1 - name | Γ] /- S2 = T2.
Γ /- {some(TX1), S2} == {some(_), T2} :- [TX1 - name | Γ] /- S2 = T2.
% ------------------------ TYPING ------------------------
Γ /- true : bool.
Γ /- false : bool.
Γ /- if(M1, M2, M3) : T2 :- Γ /- M1 : T1, Γ /- T1 = bool,
Γ /- M2 : T2, Γ /- M3 : T3, Γ /- T2 = T3.
Γ /- 0 : nat.
Γ /- succ(M1) : nat :- Γ /- M1 : T1, Γ /- T1 = nat, !.
Γ /- pred(M1) : nat :- Γ /- M1 : T1, Γ /- T1 = nat, !.
Γ /- iszero(M1) : bool :- Γ /- M1 : T1, Γ /- T1 = nat, !.
Γ /- unit : unit.
Γ /- F1 : float :- float(F1).
Γ /- M1 * M2 : float :- Γ /- M1 : T1, Γ /- T1 = float,
Γ /- M2 : T2, Γ /- T2 = float.
Γ /- X : string :- string(X).
Γ /- X : T :- x(X), gett(Γ, X, T).
Γ /- (fn(X : T1) -> M2) : (T1 -> T2_) :- [X:T1|Γ] /- M2 : T2_.
Γ /- M1 $ M2 : T12 :- Γ /- M1 : T1, simplify(Γ, T1, (T11 -> T12)),
Γ /- M2 : T2, Γ /- T11 = T2.
Γ /- (let(X) = M1 in M2) : T :- Γ /- M1 : T1, [X:T1|Γ] /- M2 : T.
Γ /- fix(M1) : T12 :- Γ /- M1 : T1, simplify(Γ, T1, (T11 -> T12)), Γ /- T12 = T11.
Γ /- inert(T) : T.
Γ /- (M1 as T) : T :- Γ /- M1 : T1, Γ /- T1 = T.
Γ /- {Mf} : {Tf} :- maplist([L = M, L : T] >> (Γ /- M : T), Mf, Tf).
Γ /- M1 # L : T :- Γ /- M1 : T1, simplify(Γ, T1, {Tf}), member(L : T, Tf).
Γ /- ({(T1, M2)} as T) : T :- simplify(Γ, T, {some(Y), T2}), Γ /- M2 : S2,
T2![(Y -> T1)] tsubst T2_, Γ /- S2 = T2_.
Γ /- (let(TX, X) = M1 in M2) : T2 :- Γ /- M1 : T1, simplify(Γ, T1, {some(_), T11}),
[X:T11, TX - tvar | Γ] /- M2 : T2.
Γ /- (fn(TX) => M2) : (all(TX) => T2) :- [TX - tvar | Γ] /- M2 : T2.
Γ /- M1![T2] : T12_ :- Γ /- M1 : T1, simplify(Γ, T1, (all(X) => T12)),
T12![(X -> T2)] tsubst T12_.
show(X : T) :- !,format('~w : ~w\n', [X, T]).
show(X :: T) :- !,format('~w :: *\n', [X]).
show(X) :- format('~w\n', [X]).
run({(TX, X)} = M, Γ, [X:some(TBody)=T12,TX-tvar|Γ])
:- tx(TX), x(X), m(M), Γ /- M : T, simplify(Γ, T, {some(_), TBody}),
Γ /- M ==>> {(_, T12)} as _, format('~w\n~w : ~w\n', [TX, X, TBody]).
run({(TX, X)} = M, Γ, [X:TBody,TX-tvar|Γ]):- tx(TX), x(X), m(M), Γ /- M : T, simplify(Γ, T, {some(_), TBody}),
format('~w\n~w : ~w\n', [TX, X, TBody]).
run(type(X), Γ, [X-tvar|Γ]) :- tx(X), show(X).
run(type(X) = T, Γ, [X::T|Γ]) :- tx(X), t(T), show(X :: T).
run(X : T, Γ, [X:T|Γ]) :- x(X), t(T), show(X : T).
run(X : T = M, Γ, [X:T=M_|Γ]) :- x(X), t(T), m(M), Γ /- M : T_, Γ /- T_ = T,
Γ /- M ==>> M_, show(X : T).
run(X = M, Γ, [X:T=M_|Γ]) :- x(X), m(M), Γ /- M : T, Γ /- M ==>> M_, show(X : T).
run(M, Γ, Γ) :- !, m(M), !, Γ /- M : T, !, Γ /- M ==>> M_, !, writeln(M_ : T).
run(Ls) :- foldl(run, Ls, [], _).
% ------------------------ TEST ------------------------
% "hello";
:- run(["hello"]).
% unit;
:- run([unit]).
% lambda x:A. x;
:- run([(fn(x : 'A') -> x)]).
% let x=true in x;
:- run([(let(x) = true in x)]).
% timesfloat 2.0 3.14159;
:- run([2.0 * 3.14159]).
% lambda x:Bool. x;
:- run([(fn(x : bool) -> x)]).
% (lambda x:Bool->Bool. if x false then true else false)
% (lambda x:Bool. if x then false else true);
:- run([(fn(x : (bool -> bool)) -> if(x $ false, true, false)) $
(fn(x : bool) -> if(x, false, true))]).
% lambda x:Nat. succ x;
:- run([(fn(x : nat) -> succ(x))]).
% (lambda x:Nat. succ (succ x)) (succ 0);
:- run([(fn(x : nat) -> succ(succ(x))) $ succ(0)]).
% T = Nat->Nat;
% lambda f:T. lambda x:Nat. f (f x);
:- run([type('T') = (nat -> nat),
(fn(f : 'T') -> fn(x : nat) -> f $ (f $ x))]).
% lambda X. lambda x:X. x;
:- run([(fn('X') => fn(x : 'X') -> x)]).
% (lambda X. lambda x:X. x) [All X.X->X];
:- run([(fn('X') => fn(x : 'X') -> x)![(all('X') => 'X' -> 'X')]]).
% {*Nat, lambda x:Nat. succ x} as {Some X, X->Nat};
:- run([{(nat, (fn(x : nat) -> succ(x)))} as {some('X'), ('X' -> nat)}]).
% {*All Y.Y, lambda x:(All Y.Y). x} as {Some X,X->X};
:- run([{((all('Y') => 'Y'), (fn(x : (all('Y') => 'Y')) -> x))} as {some('X'), ('X' -> 'X')}]).
% {x=true, y=false};
:- run([{[x = true, y = false]}]).
% {x=true, y=false}.x;
:- run([{[x = true, y = false]} # x]).
% {true, false};
:- run([{[1 = true, 2 = false]}]).
% {true, false}.1;
:- run([{[1 = true, 2 = false]} # 1]).
% {*Nat, {c=0, f=lambda x:Nat. succ x}} as {Some X, {c:X, f:X->Nat}};
:- run([{(nat, {[c = 0, f = (fn(x : nat) -> succ(x))]})} as {some('X'), {[c : 'X', f : ('X' -> nat)]}}]).
% let {X,ops} = {*Nat, {c=0, f=lambda x:Nat. succ x}} as {Some X, {c:X, f:X->Nat}}
% in (ops.f ops.c);
:- run([(let('X', ops) = {(nat, {[c = 0, f = (fn(x : nat) -> succ(x))]})} as {some('X'), {[c : 'X', f : ('X' -> nat)]}}
in ops # f $ ops # c)]).
:- halt.
まとめ
System F は全総型と存在型を持った多相的な型システムです。
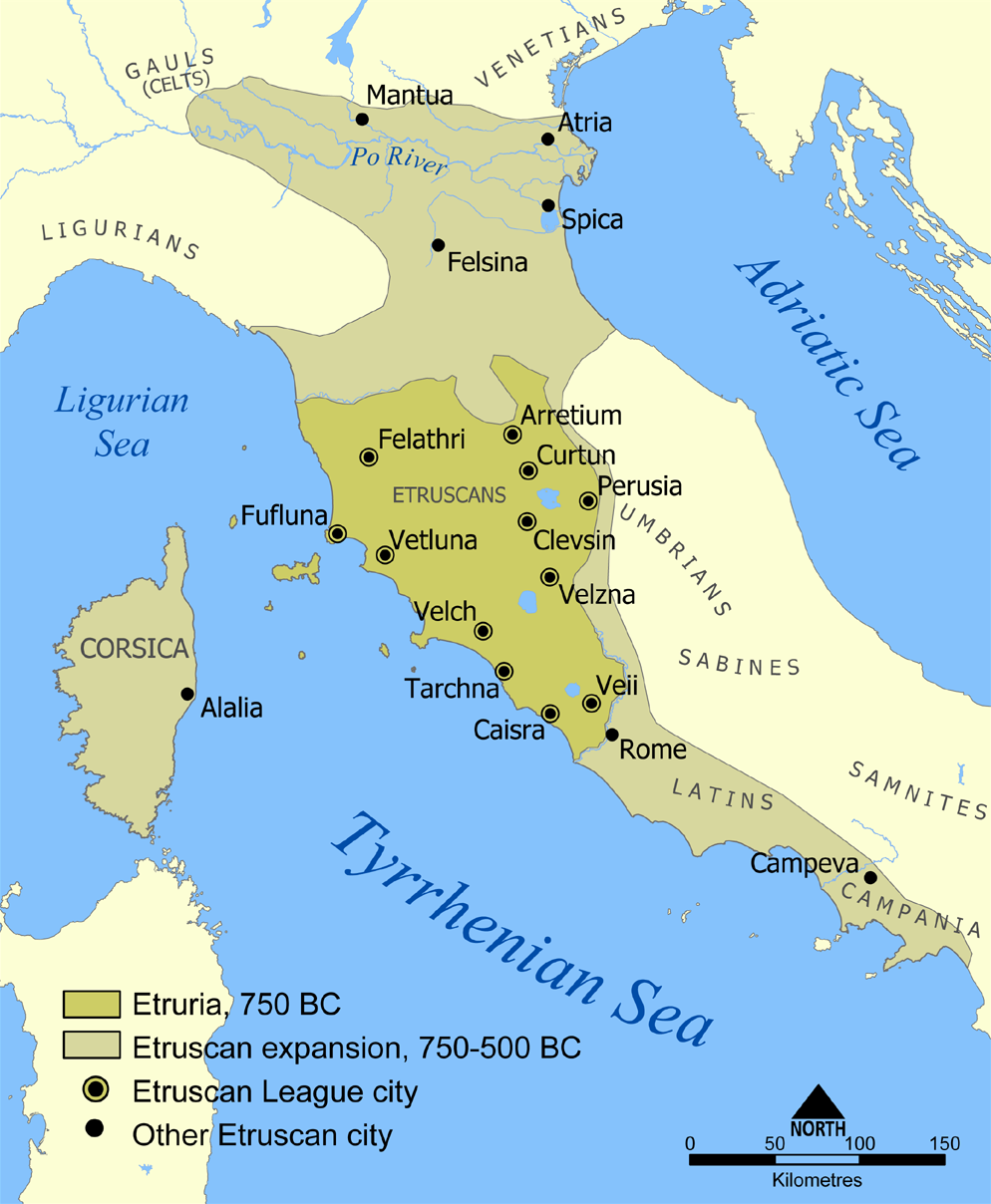
Etruria From Wikipedia, the free encyclopediaEtruria (/ɪˈtrʊəriə/; usually referred to in Greek source texts as Tyrrhenia Greek: Τυρρηνία) was a region of Central Italy, located in an area that covered part of what are now Tuscany, Lazio, and Umbria.
マールスの名前の起源はエトルリア人のマリスから来ているらしい。ギリシャの歴史家ヘロドトスによれば、エトルリア人は小アジアのリュディアからこの地にやってきたという。
小アジアとは現在のトルコのアジア部分にあたり、リュディアという国があった。リュディアでは世界で初の硬化があった。日食の戦いでは世界初の哲学者タレスによって日食が予言されており日食に恐れて休戦になったという。