More than 5 years have passed since last update.

Prolog でわかる TAPL 3日目 - 第Ⅰ部型無しの計算体系 (1)

Last updated at 2019-12-11Posted at 2019-11-29

アレース

アレースもしくはアーレース（ΑΡΗΣ、Arēs、Ἄρης, Ārēs）は、ギリシア神話に登場する神で、戦を司る[1]。ゼウスとヘーラーの子とされる[1]。オリュンポス十二神の一柱[1]。アイオリス方言ではアレウスもしくはアーレウス（Ἄρευς、Areus）とも。日本語では長母音を省略してアレスとも呼ばれる[1]。聖獣はオオカミ、イノシシで聖鳥は啄木鳥、雄鶏。聖樹はトネリコ。

本来は戦闘時の狂乱を神格化したもので、恩恵をもたらす神というより荒ぶる神として畏怖された[2]。「城壁の破壊者」の二つ名がある。戦争における栄誉や計略を表すアテーナーに対して、戦場での狂乱と破壊の側面を表す[2]。その性格も粗野で残忍、かつ不誠実であった。

中略

ローマ神話のマールスに相当し[1]、また火星と同一視される。このため黄道上に位置し火星とよく似た赤い輝きを放つ天体であるさそり座のα星はアンタレス[注 1]と呼ばれる[4][5]。火星の衛星フォボスとダイモスはアレースの子の名から採られている。

Wikipedia アレースより

今日は３，４章の型無し算術式の実装を見ていきます。

Boolとif式がある者に加え、
型無し術式ではペアノ自然数を用いた算術の内足し算と引き算のみが実装されています。
ペアノ自然数は何もない世界に論理的に数字を作り出す際に使われる0から始まる自然数のことです。
0は0ですが、1はsucc(0)、2はsucc(succ(0))、3はsucc(succ(succ(0))) のように表すことで自然数を表します。
ペアの自然数は CPU の演算能力を使った処理系よりも動作が遅いですが、論理的単純さは勝っています。

図3-1.ブール値(B)

B(型無し)

構文

t ::=                項：
  true               定数真
  false              定数偽
  if t then t else t 条件式

v::=                 値：
  true               定数真
  false              定数偽

評価 t ==> t’

if true then t2 else t3 ==> t2   (E-IfTrue)

if false then t2 else t3 ==> t3  (E-IfFalse)

t1 ==> t1’
-------------------------------- (E-If)
if t1 then t2 else t3
==> if t1’ then t2 else t3

この図は Bool のみがある最も簡単な言語です。以下のようにPrologで書くことができます:

b.pl

:- op(1200,xfx,::=).
:- op(920, xfx, ['→', '↠']).
:- op(650,xfx,∈).
:- op(250,yf,*).
G∈{G}. G∈(G|_). G∈(_|G1):-G∈G1. G∈G.
syntax(S/[S2],AEs) :- compound_name_arguments(AEs,A,Es),syntax(S,A),syntax(S2,Es).
syntax(G,E):-G=..[O|Gs],E=..[O|Es],maplist(syntax,Gs,Es),!.
syntax(G,E):-(G::=Gs),!,G1∈Gs,syntax(G1,E),!.
syntax(i,I):-integer(I),!.
syntax(x,I):- atom(I),!.
syntax(E*,Ls) :- maplist(syntax(E),Ls).

% 構文

t ::=             % 項:
      true        % 真
    | false       % 偽
    | if(t, t, t) % 条件式
    .
v ::=             % 値:
      true        % 真
    | false       % 偽
    .

% 評価 t → t'

if(true, T2, _) → T2.                         % (E-IfTrue)
if(false, _, T3) → T3.                        % (E-IfFalse)
if(T1, T2, T3) → if(T1_, T2, T3) :- T1 → T1_.% (E-If)

T ↠ T_                           :- T → T1, T1 ↠ T_.
T ↠ T.

% Main

run(T, Γ/[T_|Ts], Γ/Ts) :- !, syntax(t,T), !, T ↠ T_, !.
run(Ls,Ts)      :- foldl(run, Ls, []/Ts_, _/[]),!,Ts=Ts_.
run(Ls)         :- run(Ls,Ts),writeln(Ts).

:- begin_tests(b).
  test(true) :- run([true],[true]).
  test(if)   :- run([if(false, true, false),if(true,true,false)],[false,true]).
  test(if)   :- run([if(false, true, false),if(if(false, true, false),true,if(true, true, false))],[false,true]).
:- end_tests(b).
:- run_tests.
:- halt.

図3-2.算術式(NB)

B N(型無し) B(図3-1)の拡張

新しい構文形式

t ::= …    項：
  0         定数ゼロ
  succ t    後者値
  pred t    前者値
  iszero t  ゼロ判定
v ::= …    値：
  nv        数値

nv ::=      数値：
  0         ゼロ
  succ nv   後者値

新しい評価規則 t ==> t’

t1 ==> t1’
------------------------------------ (E-Succ)
succ t1 ==> succ t1’

pred 0 ==> 0                         (E-PredZero)

pred(succ nv1) ==> nv1               (E-PredSucc)

t1 ==> t1’
------------------------------------ (E-Pred)
pred t1 ==> pred t1’

iszero 0 ==> true                    (E-IsZeroZero)

iszero(succ nv1) ==> false.          (E-IsZeroSucc)

t1 ==> t1’
------------------------------------ (E-Zero)
iszero t1 ==> iszero t1’

こちらの図はBを算術式について拡張するための図です。arith.plでまとめて実装してあります。

図3-bigstep評価

v ⇓ v                                     (B-Value)

t1 ⇓ true   t2 ⇓ v2
------------------------------------------ (B-IfTrue)
if t1 then t2 else t3 ⇓ v2

t1 ⇓ false   t3 ⇓ v3
------------------------------------------ (B-IfFalse)
if t1 then t2 else t3 ⇓ v3

t1 ⇓ nv1
------------------------------------------ (B-Succ)
succ t1 ⇓ succ nv1

t1 ⇓ 0
------------------------------------------ (B-PredZero)
pred t1 ⇓ 0

t1 ⇓ succ nv1
------------------------------------------ (B-PredSucc)
pred t1 ⇓ nv1

t1 ⇓ 0
------------------------------------------ (B-IszeroZero)
iszero t1 ⇓ true

t1 ⇓ succ nv1
------------------------------------------ (B-IszeroSucc)
iszero t1 ⇓ false

この図は、ビックステップ評価器として実装したものです。以下にコードを示します:

arith_big.pl はここをクリック

arith_big.pl

% ------------------------   SYNTAX  ------------------------
:- op(1200,xfx,[::=,--]).
:- op(920, xfx, [⇓]).
:- op(650,xfx,∈).
:- op(250,yf,*).
G∈{G}. G∈(G|_). G∈(_|G1):-G∈G1. G∈G.
syntax(S/[S2],AEs) :- compound_name_arguments(AEs,A,Es),syntax(S,A),syntax(S2,Es).
syntax(G,E):-G=..[O|Gs],E=..[O|Es],maplist(syntax,Gs,Es),!.
syntax(G,E):-(G::=Gs),!,G1∈Gs,syntax(G1,E),!.
syntax(i,I):-integer(I),!.
syntax(x,I):- atom(I),!.
syntax(E*,Ls) :- maplist(syntax(E),Ls).
term_expansion(A--B,B:-A).

m ::=             % 項:
      true        % 真
    | false       % 偽
    | if(m, m, m) % 条件式
    | 0           % ゼロ
    | succ(m)     % 後者値
    | pred(m)     % 前者値
    | iszero(m)   % ゼロ判定
    .
v ::=             % 値:
      true        % 真
    | false       % 偽
    | nv          % 数値
    .
nv::=             % 数値:
      0           % ゼロ
    | succ(nv)    % 後者値
    .

% ------------------------   EVALUATION  ------------------------

syntax(v,V)
--%---------------------------------------- (B-Value)
V ⇓ V.

T1 ⇓ true,   T2 ⇓ V2
--%---------------------------------------- (B-IfTrue)
if(T1, T2, _) ⇓ V2.

T1 ⇓ false,   T3 ⇓ V3
--%---------------------------------------- (B-IfFalse)
if(T1, _, T3) ⇓ V3.

T1 ⇓ NV1
--%---------------------------------------- (B-Succ)
succ(T1) ⇓ succ(NV1).

T1 ⇓ 0
--%---------------------------------------- (B-PredZero)
pred(T1) ⇓ 0.

T1 ⇓ succ(NV1)
--%---------------------------------------- (B-PredSucc)
pred(T1) ⇓ NV1.

T1 ⇓ 0
--%---------------------------------------- (B-IszeroZero)
iszero(T1) ⇓ true.

T1 ⇓ succ(NV1), syntax(nv,NV1)
--%---------------------------------------- (B-IszeroSucc)
iszero(T1) ⇓ false.

% ------------------------   MAIN  ------------------------

run(M, Γ/[M_|Ms], Γ/Ms) :- !, syntax(m,M), !, M ⇓ M_, !.
run(Ls,Ms)      :- foldl(run, Ls, []/Ms_, _/[]),!,Ms=Ms_.
run(Ls)         :- run(Ls,Ms),writeln(Ms).

% ------------------------   TEST  ------------------------

:- begin_tests(arith).
  test(true) :- run([true],[true]).
  test(if)   :- run([if(false, true, false),if(true,true,false)],[false,true]).
  test(nat)  :- run([0,succ(0),succ(succ(0))],[0,succ(0),succ(succ(0))]).
  test(pred) :- run([pred(succ(0)),pred(succ(succ(0))),succ(pred(0))],[0,succ(0),succ(0)]).
  test(iszero):- run([iszero(pred(succ(succ(0))))],[false]).
  test(iszero):- run([iszero(pred(pred(succ(succ(0)))))],[true]).
  test(iszero):- run([iszero(0)],[true]).
  test(expr):- run([if(true, succ(pred(0)), 0)],[succ(0)]).
  test(expr):- run([if(true, succ(succ(0)), 0)],[succ(succ(0))]).
  test(expr):- run([if(true, succ(pred(succ(0))), 0)],[succ(0)]).
:- end_tests(arith).
:- run_tests.
:- halt.

実装

arith.pl

以下に arith.pl の実装を示します:

プログラムの全体を見る

arith.pl

% ------------------------   SYNTAX  ------------------------
:- op(1200,xfx,::=).
:- op(920, xfx, ['→', '↠']).
:- op(650,xfx,∈).
:- op(250,yf,*).
G∈{G}. G∈(G|_). G∈(_|G1):-G∈G1. G∈G.
syntax(S/[S2],AEs) :- compound_name_arguments(AEs,A,Es),syntax(S,A),syntax(S2,Es).
syntax(G,E):-G=..[O|Gs],E=..[O|Es],maplist(syntax,Gs,Es),!.
syntax(G,E):-(G::=Gs),!,G1∈Gs,syntax(G1,E),!.
syntax(i,I):-integer(I),!.
syntax(x,I):- atom(I),!.
syntax(E*,Ls) :- maplist(syntax(E),Ls).

m ::=             % 項:
      true        % 真
    | false       % 偽
    | if(m, m, m) % 条件式
    | 0           % ゼロ
    | succ(m)     % 後者値
    | pred(m)     % 前者値
    | iszero(m)   % ゼロ判定
    .
n ::=             % 数値:
      0           % ゼロ
    | succ(n)     % 後者値
    .
v ::=             % 値:
      true        % 真
    | false       % 偽
    | n           % 数値
    .

% ------------------------   EVALUATION  ------------------------

if(true, M2, _) → M2.
if(false, _, M3) → M3.
if(M1, M2, M3) → if(M1_, M2, M3) :- M1 → M1_.
succ(M1) → succ(M1_)             :- M1 → M1_.
pred(0) → 0.
pred(succ(N1)) → N1              :- syntax(n,N1).
pred(M1) → pred(M1_)             :- M1 → M1_.
iszero(0) → true.
iszero(succ(N1)) → false         :- syntax(n,N1).
iszero(M1) → iszero(M1_)         :- M1 → M1_.
M ↠ M_                           :- M → M1, M1 ↠ M_.
M ↠ M.

% ------------------------   MAIN  ------------------------

run(M, Γ/[M_|Ms], Γ/Ms) :- !, syntax(m,M), !, M ↠ M_, !.
run(Ls,Ms)      :- foldl(run, Ls, []/Ms_, _/[]),!,Ms=Ms_.
run(Ls)         :- run(Ls,Ms),writeln(Ms).

% ------------------------   TEST  ------------------------

:- begin_tests(arith).
  test(true) :- run([true],[true]).
  test(if)   :- run([if(false, true, false),if(true,true,false)],[false,true]).
  test(nat)  :- run([0,succ(0),succ(succ(0))],[0,succ(0),succ(succ(0))]).
  test(pred) :- run([pred(succ(0)),pred(succ(succ(0))),succ(pred(0))],[0,succ(0),succ(0)]).
  test(iszero):- run([iszero(pred(succ(succ(0))))],[false]).
  test(iszero):- run([iszero(pred(pred(succ(succ(0)))))],[true]).
  test(iszero):- run([iszero(0)],[true]).
  test(expr):- run([if(true, succ(pred(0)), 0)],[succ(0)]).
  test(expr):- run([if(true, succ(succ(0)), 0)],[succ(succ(0))]).
  test(expr):- run([if(true, succ(pred(succ(0))), 0)],[succ(0)]).
:- end_tests(arith).
:- run_tests.
:- halt.

arith_macro.pl Prolog実装(マクロバージョン)

term_expansion/2 いわゆるマクロ的な項書換えを用いたバージョンは以下のとおりです:

プログラムの全体を見る

arith_macro.pl

% ------------------------   SYNTAX  ------------------------
:- op(1200,xfx,[::=,--]).
:- op(920, xfx, ['→', '↠']).
:- op(650,xfx,∈).
:- op(250,yf,*).
G∈{G}. G∈(G|_). G∈(_|G1):-G∈G1. G∈G.
syntax(S/[S2],AEs) :- compound_name_arguments(AEs,A,Es),syntax(S,A),syntax(S2,Es).
syntax(G,E):-G=..[O|Gs],E=..[O|Es],maplist(syntax,Gs,Es),!.
syntax(G,E):-(G::=Gs),!,G1∈Gs,syntax(G1,E),!.
syntax(i,I):-integer(I),!.
syntax(x,I):- atom(I),!.
syntax(E*,Ls) :- maplist(syntax(E),Ls).
term_expansion(A--B,B:-A).

m ::=             % 項:
      true        % 真
    | false       % 偽
    | if(m, m, m) % 条件式
    | 0           % ゼロ
    | succ(m)     % 後者値
    | pred(m)     % 前者値
    | iszero(m)   % ゼロ判定
    .
n ::=             % 数値:
      0           % ゼロ
    | succ(n)     % 後者値
    .
v ::=             % 値:
      true        % 真
    | false       % 偽
    | n           % 数値
    .

% ------------------------   EVALUATION  ------------------------

!
--%-------------------------------- (E-IfTrue)
if(true, M2, _) → M2.

!
--%-------------------------------- (E-IfFalse)
if(false, _, M3) → M3.

M1 → M1_
--%-------------------------------- (E-If)
if(M1, M2, M3) → if(M1_, M2, M3).

M1 → M1_
--%-------------------------------- (E-Succ)
succ(M1) → succ(M1_).

!
--%-------------------------------- (E-PredZero)
pred(0) → 0.

syntax(n,N1)
--%-------------------------------- (E-PredSucc)
pred(succ(N1)) → N1.

M1 → M1_
--%-------------------------------- (E-Pred)
pred(M1) → pred(M1_).

!
--%-------------------------------- (E-IsZeroZero)
iszero(0) → true.

syntax(n,N1)
--%-------------------------------- (E-IsZeroSucc)
iszero(succ(N1)) → false.

M1 → M1_
--%-------------------------------- (E-IsZero)
iszero(M1) → iszero(M1_).

M → M1, M1 ↠ M_
--%-------------------------------- (E-All1)
M ↠ M_.

M ↠ M.                           % (E-All2)

% ------------------------   MAIN  ------------------------

run(M, Γ/[M_|Ms], Γ/Ms) :- !, syntax(m,M), !, M ↠ M_, !.
run(Ls,Ms)      :- foldl(run, Ls, []/Ms_, _/[]),!,Ms=Ms_.
run(Ls)         :- run(Ls,Ms),writeln(Ms).

% ------------------------   TEST  ------------------------

:- begin_tests(arith).
  test(true) :- run([true],[true]).
  test(if)   :- run([if(false, true, false),if(true,true,false)],[false,true]).
  test(nat)  :- run([0,succ(0),succ(succ(0))],[0,succ(0),succ(succ(0))]).
  test(pred) :- run([pred(succ(0)),pred(succ(succ(0))),succ(pred(0))],[0,succ(0),succ(0)]).
  test(iszero):- run([iszero(pred(succ(succ(0))))],[false]).
  test(iszero):- run([iszero(pred(pred(succ(succ(0)))))],[true]).
  test(iszero):- run([iszero(0)],[true]).
  test(expr):- run([if(true, succ(pred(0)), 0)],[succ(0)]).
  test(expr):- run([if(true, succ(succ(0)), 0)],[succ(succ(0))]).
  test(expr):- run([if(true, succ(pred(succ(0))), 0)],[succ(0)]).
:- end_tests(arith).
:- run_tests.
:- halt.

まとめ

プログラミング言語は関数が引数を1つしか取らないため簡単な言語なので型理論の構築によく使われています。
プログラミング言語はMBNFにより構文定義され、操作的意味論により意味づけされます。

今日は手始めに算術式の意味を考え、実装しました。

評価規則がプログラムをどう操作するかを定義します。
スモールステップ評価器の実装は速くはありませんが、1ステップごとの状態を表すことが出来るのでマルチスレッドで動かすような状態も表すことが出来ます。
ビックステップ評価器の実装は高速ですが、平行、並列な計算状態を表すことはできません。

Yggdrasil
From Wikipedia, the free encyclopedia

For other uses, see Yggdrasil (disambiguation).
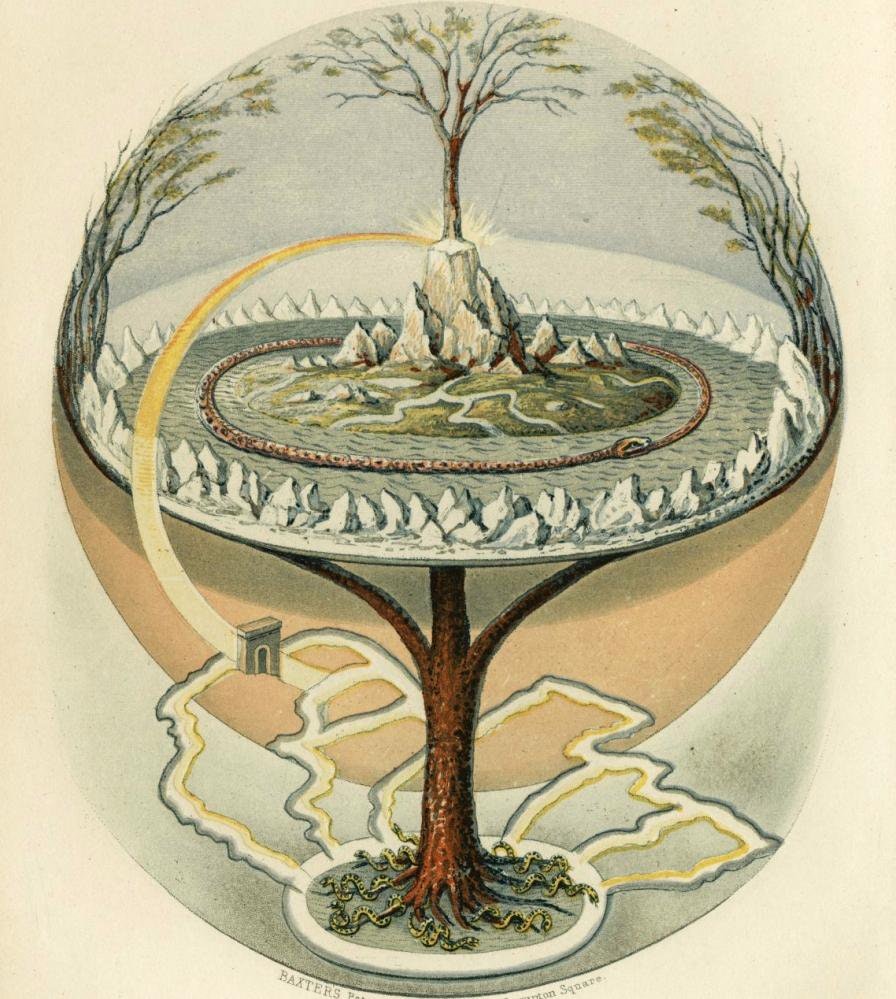
"The Ash Yggdrasil" (1886) by Friedrich Wilhelm Heine

Yggdrasil (from Old Norse Yggdrasill) is an immense mythical tree that plays a central role in Norse cosmology, where it connects the Nine Worlds.

Yggdrasil is attested in the Poetic Edda, compiled in the 13th century from earlier traditional sources, and the Prose Edda, written in the 13th century by Snorri Sturluson. In both sources, Yggdrasil is an immense ash tree that is center to the cosmos and considered very holy. The gods go to Yggdrasil daily to assemble at their things, traditional governing assemblies. The branches of Yggdrasil extend far into the heavens, and the tree is supported by three roots that extend far away into other locations; one to the well Urðarbrunnr in the heavens, one to the spring Hvergelmir, and another to the well Mímisbrunnr. Creatures live within Yggdrasil, including the dragon Níðhöggr, an unnamed eagle, and the stags Dáinn, Dvalinn, Duneyrr and Duraþrór.

Conflicting scholarly theories have been proposed about the etymology of the name Yggdrasill, the possibility that the tree is of another species than ash, its connection to the many sacred trees and groves in Germanic paganism and mythology, and the fate of Yggdrasil during the events of Ragnarök.

World tree
From Wikipedia, the free encyclopedia

This article is about the religious motif. For other uses, see World Tree (disambiguation).

The world tree is a motif present in several religions and mythologies, particularly Indo-European religions, Siberian religions, and Native American religions. The world tree is represented as a colossal tree which supports the heavens, thereby connecting the heavens, the terrestrial world, and, through its roots, the underworld. It may also be strongly connected to the motif of the tree of life, but it is the source of wisdom of the ages.

Specific world trees include égig érő fa in Hungarian mythology, Ağaç Ana in Turkic mythology, Modun in Mongol mythology, Yggdrasil (or Irminsul) in Norse (including Germanic) mythology, the oak in Slavic, Finnish and Baltic, Iroko in Yoruba religion,[citation needed] Jianmu in Chinese mythology, and in Hindu mythology the Ashvattha (a Ficus religiosa).

どうでもいい筆者のつぶやき

聖樹がトネリコでトルネコでも鳥猫でもなくて、日本語では、世界樹とか言われるらしく、面白いなと思って貼っつけてみた。アリスとアレスってなんか似てるなとかだな。哲学者は、、、

PrologAdvent Calendar 2019

Day 3

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up

Prolog でわかる TAPL 3日目 - 第Ⅰ部 型無しの計算体系 (1)

図3-1.ブール値(B)

図3-2.算術式(NB)

図3-bigstep評価

実装

arith.pl

arith_macro.pl Prolog実装(マクロバージョン)

まとめ

Prolog でわかる TAPL 3日目 - 第Ⅰ部型無しの計算体系 (1)