極限
数列または関数がある値に近づくとき、その値を「数列の極限」または「関数の極限」といいます。主に微分で使うのは「関数の極限」になります。
関数の極限
定義
関数f(x)において、xがaと異なる値を取りながらaに限りなく近づくとき、f(x)がある一定の値bに限りなく近づく場合、
\lim_{x \to a}f(x) = b \\
と書き、xがaに限りなく近づくときのf(x)の極限値はbであるといいます。
考え方
例として、f(x)=2x+1において$lim_{x→1}f(x)$がいくつになるか考えてみましょう。
例えば、xを0.9からスタートして、0.99,0.999,0.9999,…と1に近づけていくと
f(0.9) = 2 × 0.9 + 1 = 2.8 \\
f(0.99) = 2 × 0.99 + 1 = 2.98 \\
f(0.999) = 2 × 0.999 + 1 = 2.998 \\
f(0.9999) = 2 × 0.9999 + 1 = 2.9998 \\
となり、f(x)の値は3に近づいていくことが分かります。
多項式の極限値は、関数値（単に値を代入したもの）と等しくなります。
例題
次の極限値を求めなさい。(+0：xが0よりも大きい値を取りながら0に近づく)
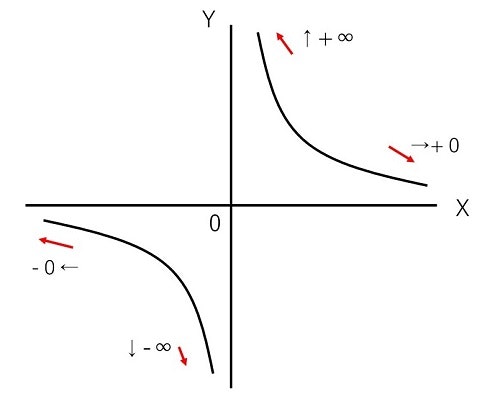
\lim_{x \to +0} \frac{1}{x}
次の図はy=1/xのグラフです。
この図から、以下のことが分かります。
\lim_{x \to +0} \frac{1}{x} = \infty \\
\lim_{x \to -0} \frac{1}{x} = -\infty \\
\lim_{x \to +\infty} \frac{1}{x} = 0 \\
\lim_{x \to -\infty} \frac{1}{x} = 0 \\
練習問題
1. \lim_{x \to 3} (x^2 + 2x -3) \\
2. \lim_{x \to 1} \frac{x^2 -3x +2}{x-1} \\
3. \lim_{x \to 0} \frac{x^2-2x}{x} \\
4. \lim_{x \to +\infty} \frac{2}{x-1}\\
$$1. \lim_{x \to 3} (x^2 + 2x -3) = (3^2 + 2×3 -3) = 12$$
$$2. \lim_{x \to 1} \frac{x^2 -3x +2}{x-1} = \lim_{x \to 1}\frac{(x-2)(x-1)}{x-1} = \lim_{x \to 1}(x-2) = -1$$
$$3. \lim_{x \to 0} \frac{x^2-2x}{x} = \lim_{x \to 0} (x -2) = -2$$
$$4. \lim_{x \to +\infty} \frac{2}{x-1} = 0$$
微分係数
区間を狭くしていったときの平均変化率（傾き）の値のことを、微分係数をいいます。
定義
関数 y = f(x) の x = a における微分係数を f’(a) で表わし，次の式で定義します。
1. f'(a)=\lim_{b \to a} \frac{f(b) -f(a)}{b-a} \\
2. f'(a)=\lim_{h \to 0} \frac{f(a+h) -f(a)}{h} \\
平均変化率
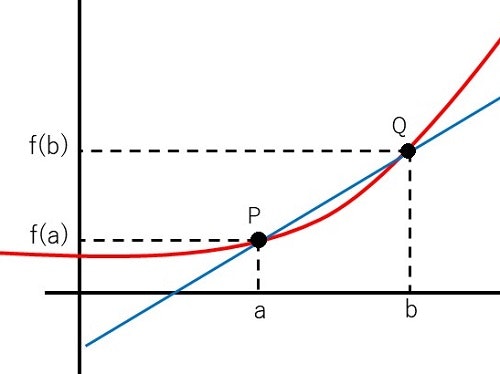
下の図にように、関数f(x)のxの値が、aからbに変化したとき、f(x)の変化量をxの増加量b-aで割ったものを平均変化率といい、直線PQの傾きになります。この平均変化率(傾き)を式で表すと、
\frac{f(b) -f(a)}{b-a} \\
となります。
微分係数
微分係数とは、区間を狭くしていったときの平均変化率（傾き）の値のことをいいます。つまり、x = aでの微分係数は、bをaに限りなく近づけたものなので、
f'(a)=\lim_{b \to a} \frac{f(b) -f(a)}{b-a} \\
が微分係数となります。
また、「bをaに近づける」ではなく「b-aを0に近づける」と考えることできます。差を0に近づけることと同じなので、h=b-aとすると、b=a+hとなり、
f'(a)=\lim_{h \to 0} \frac{f(a+h) -f(a)}{h} \\
のように変形できます。どちらも同じ意味の式ですが、こちらが使われることが多いです。
例題
f(x)=x^2のx=-1での微分係数を求めよ。
微分係数は
\begin{align}
f'(-1)&=\lim_{h \to 0} \frac{(-1+h)^2 - (-1)^2}{h} \\
&=\lim_{h \to 0} \frac{(1-2h+h^2) - (-1)^2}{h}\\
&=\lim_{h \to 0} \frac{-2h+h^2}{h}\\
&=\lim_{h \to 0} (-2+h)\\
&=-2
\end{align}
と求められます。
練習問題
1.f(x)=x^2のとき、f'(3)を求めなさい。
2.f(x)=x^2-xのとき、f'(a)を求めなさい。
$$1. f'(3)=\lim_{h \to 0} \frac{f(3+h)-f(3)}{h} =\lim_{h \to 0} \frac{(3+h)^2-3^2}{h}=\lim_{h \to 0} \frac{6h+h^2}{h}=\lim_{h \to 0} (6+h)=6$$
$$2. f'(a)=\lim_{h \to 0} \frac{f(a+h)-f(a)}{h}
=\lim_{h \to 0} \frac{{(a+h)^2-(a+h)}-(a^2-a)}{h}
=\lim_{h \to 0} \frac{{(a^2+2ah+h^2)-(a+h)}-(a^2-a)}{h}
=\lim_{h \to 0} \frac{2ah-h+h^2}{h}
=\lim_{h \to 0} {2a-1+h}
=2a-1
$$