結論
とりあえず使える(整数計画問題に直せばよい)。ただし効率がいいかはよく知らない。
はじめに
この記事は、私が11月14日に「わんくま同盟 名古屋勉強会#37」で発表した内容の補足記事となります。
取り扱う問題
「SATソルバー」というソフトウェアがある。これは変数を含む論理式(trueとfalseの組み合わせからなる式。演算子としてand, or, notなどを使う)を与えたときに、論理式全体がtrueになるような変数の組み合わせが存在すればそれを一つ返し、なければ「組み合わせは存在しない」と答えてくれるものである。
例えば数独のような「所定の枠が存在して値を埋めていく(決定すべき値の数が有限である)タイプのパズル」を、適切な論理式で書くことで、あとは自動的に解かせるということも可能である(論理式が膨大になるケースもあるので、適切な時間で解けるとは限らない)。上記発表での発表資料で概要を解説しています。
例題
(A or B) and ((not A) or C) and ((not B) or (not C))をtrueにする変数A, B, Cの組み合わせは存在する?
この問題は変数の数が少ないので手計算でも解けるが、これがもっと多い変数になっても解いてくれるのがSATソルバーというわけである。ただSATソルバーを使ったとしても、一般には計算時間が爆発して、あまりに多い変数になると解けないことに注意。
例題の答え
組み合わせは存在する。まず上記の式は、(A or B), ((not A) or C), ((not B) or (not C))のすべてがtrueになれば、全体もtrueとなることに注意する。
Aがtrueだと仮定する。このとき、
-
(A or B)は無条件にtrueになる。 -
((not A) or C)は、Cがtrueのときのみtrueになる。 -
((not B) or (not C))は、Cがtrueと仮定すると、Bがfalseのときのみtrueになる。
以上より、(A, B, C) = (true, false, true)のときこの式はtrueになる。
同様に、Aがfalseだと仮定すると、(A, B, C) = (false, true, false)のときこの式はtrueになる。
今回のテーマ
さて、Excelには「ソルバー」機能がある。「ソルバー」とは一般に、所定の条件を満たす問題を与えると自動的にそれを解いてくれる(SATソルバーなら論理式)ものであるのだが、Excelの場合は値の最大化・最小化や特定の値にすることのみが扱えることになっており、SATソルバーとしての使い方、はぱっと見た感じでは少なくとも意識されてはいない。
ただ、値の最大化・最小化ができるということはSATソルバーのような「1つ答えを見つける」こともできるかも?と思い検討したのがこちらである。
解き方
1. 連言標準形に直す
まず、扱う論理式を連言標準形に直す。
連言標準形とは、上記の例題のように、(X1 or X2 or ...) and (Y1 or Y2 or ...) and ...という形をしている式である。ただしX1, X2, ..., Y1, Y2, ... は「変数」か「(not 変数)」のどちらかしか書けない(「リテラル」と呼ばれる)とする。
連言標準形への直し方は上記リンク(Wikipedia)を参照されたい。ただし直すことで式が大きくなる場合もあるので、最初から連言標準形で書けるならそれが望ましい。
例えば、(A and B) or (C and D)は連言標準形ではない。これを連言標準形にするには以下のようにする。
(A and B) or (C and D)
= (A or (C and D)) and (B or (C and D)) # 分配法則
= ((A or C) and (A or D)) and ((B or C) and (B or D)) # 分配法則
= (A or C) and (A or D) and (B or C) and (B or D) # 結合法則
2. trueを1、falseを0とみなし、不等式で表現する
続いて、trueを1、falseを0とみなし、(X1 or X2 or ...)の部分ごと(andで区切られたそれぞれの部分)が成り立つ条件を不等式で書く。すなわち、これらの不等式がすべて成り立っていれば所望の結果が得られることになる。
このとき、
- 各不等式において、リテラルは必ずorで結ばれている、すなわちどれか一つでも1であればよいので、「[変数の和] >= 1」とかける
-
(not X) = 1-Xとかける
ことがポイントである。
例:(A or B) and ((not A) or C) and ((not B) or (not C))の場合、対応する式は以下の通りとなる。
| 論理式 | 対応する不等式 |
|---|---|
A or B |
A + B >= 1 |
(not A) or C |
(1-A) + C >= 1 |
(not B) or (not C) |
(1-B) + (1-C) >= 1 |
これらの不等式がすべて成り立つA, B, Cを、「A, B, Cは0か1を取る」という条件のもとで見つけることになる。
3. Excelのソルバーで、「これらの不等式がすべて成り立つ」ことを表現する
上記のように式を立てたら、これをExcelに与える。具体的には、以下のセルを作り、それをソルバーの条件指定に記入する。
- 1つの変数を表すセル(A, B, C)。
- これらは0か1を取るように設定する必要がある。Excelなら、ソルバーのオプションにおいて「制約条件」→「追加(変更)」→真ん中を「データ」に設定→右側が「バイナリ」になればOK。LibreOfficeなら、ソルバーのオプションにおいて「制限条件」→「演算子」で「バイナリ」を選択。
- 条件の左辺を表すセル("A + B" など)。これは、上記の「1つの変数を表すセル」のものを参照して作る(例えば、Aの値をセルB4、Bの値をセルB5に書くことにした場合、"A + B"を表すセルには「=B4+B5」と書く)。
- 条件の右辺を表すセル。この例では一律で1になる。
- ダミーのセル。最大化や最小化などしかできないため、その対象となるセルをダミーで作成する。変数A(BでもCでもよいが)の値を参照するようにするのが簡単。
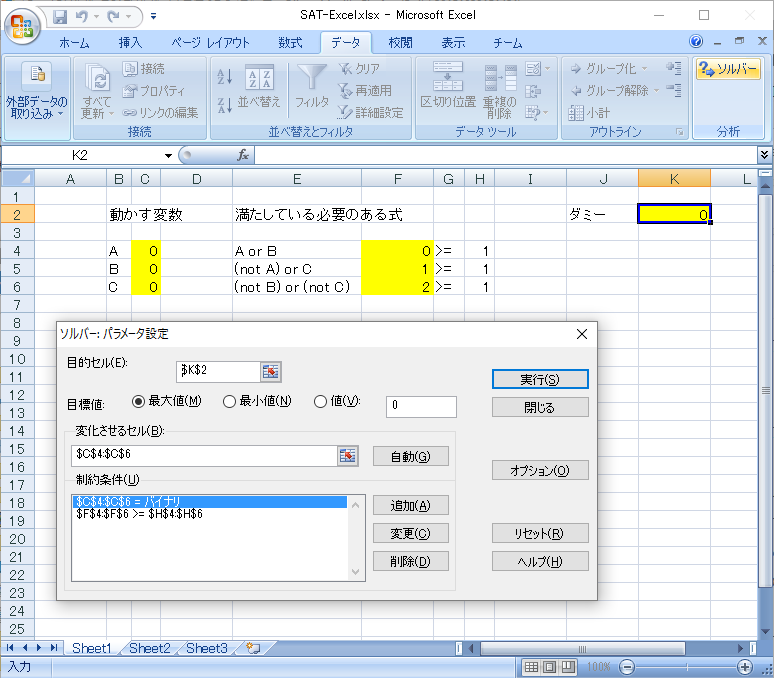
上記の(A or B) and ((not A) or C) and ((not B) or (not C))を入力したものはこちら。xlsxファイル odsファイル
Excelでの例 (xlsxファイル)
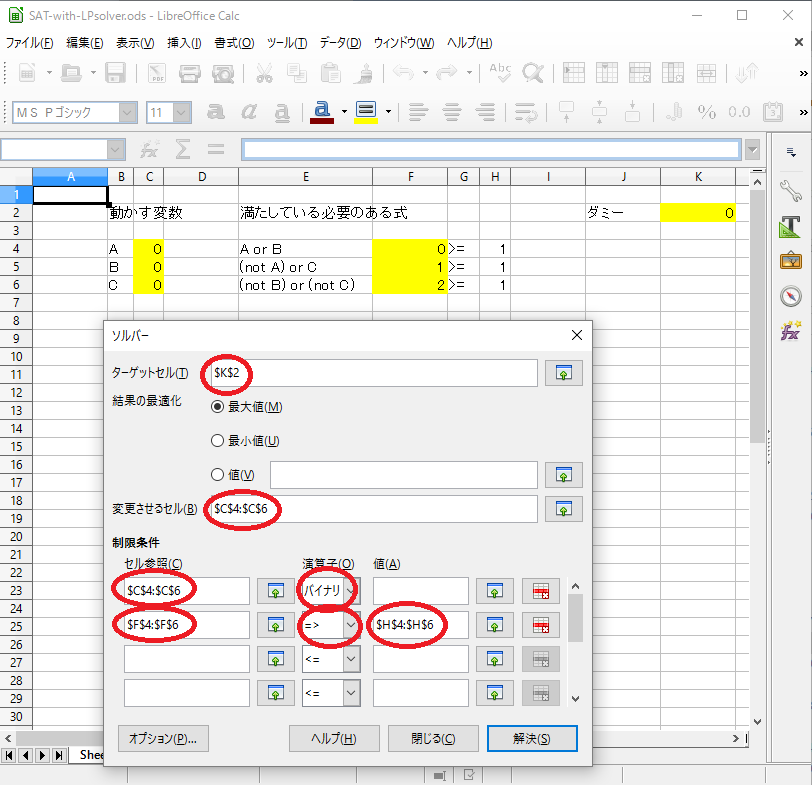
LibreOfficeでの例 (odsファイル)
注意
- Excelではソルバーに条件を与えてファイルを保存するとその条件も保存される一方、LibreOfficeは保存されない。上記のファイルをダウンロードして試される方は、スクリーンショットに提示した内容を手動で入力していただくようお願いします。
- いつからか(2007から?)、Excelは標準ではソルバーが有効化されていないため、有効にしておく必要があります。ウィンドウ左上のOfficeアイコン→「Excelのオプション」→「アドイン」→「設定」→「ソルバー アドイン」にチェックを入れて「OK」
- LibreOfficeでは、ソルバーを起動しようとすると「Java Runtime 環境(JRE)が必要です」というエラーになる場合があります。対処法(Windowsの場合)はこちら:LibreOfficeをインストールするときの注意点: LibreOfficeで行こう!
補足
Excelなどのソルバーは、「不等式でかける条件を満たす」「変数が整数に限定された」最大化・最小化問題を解く機能を備えている。特に上記のようにして得られる式は、不等式で書かれた条件が線形の式(定数×変数 + 定数×変数 + … とかける式)であり、整数計画問題と呼ばれる問題にあたる。これは一般には計算時間が爆発するものの、多くの高速化手法が検討されている分野であり、Excelのソルバー以外にもこれを解くためのソルバーが多数存在する。例えばオープンソースのGLPKとか。
おわりに
一度「整数の不等式」を経由することにはなりますが、ExcelをSATソルバーとして使うこともできるので、手軽に試したい方はいかがでしょうか。