MATLABの隠れたデータ型？ コンマ区切りリスト

はじめに

この記事では，MATLABの「コンマ区切りリスト」について紹介しています．コンマ区切りリストはデータ型ではないないのですが，そのようなモノとして意識することでMATLABの振る舞いがちょっとだけわかりやすくなったりします．

※本記事の内容はMATLAB R2020b の仕様に基づいています．

コンマ区切りリストって？

聞いたことあります？自分もごく最近までこの名前は知りませんでした．MATLABでプログラムを組んでいると，コンマ「,」で区切って変数を並べることってありますよね，例えば関数の引数．

Code

c = plus(1,2);

上の1,2の部分が「コンマ区切りリスト」です．また，コマンドラインで >> 1, 2と入力すると，答が返ってきます．この 1,2 もコンマ区切りリスト．ちなみに>> 1 2はエラーになります．

Code

1,2

Output

ans = 1
ans = 2

また，関数の返値を受ける際にもコンマ区切りリストを使っていますね．下の phi, rho がそれです．

Code

[phi, rho] = cart2pol(2,2);

返値を複数持つ関数は，それらの返値をカンマ区切りリストとして返します．それを受ける側もカンマ区切りリストとして受けるわけです．それならば

Code(Display)

phi, rho = cart2pol(2,2);

のように書くべきかなぁとも思うのですが，MATLABでは文をカンマで区切ることが許されていているわけで，そのへんの曖昧さを回避するために[]でくくることにしたのではないかなと想像してます．また，次のようにカンマ区切りリストを直接代入することは出来ないみたいですね．

Code(Display)

[a,b] = 1,2

たぶん，上の例だと，文として[a,b] = 1までが解釈されて例外が発生して，その後でカンマで区切られた単項 2 が解釈されるのでしょう．また，解釈の区切りの優先順位をつけようと，(1,2) の様に括弧でくくることも出来ませんし，さらに，大括弧[]で囲むと，ご存じのように２要素のベクトルになってしまいます．

このように，コンマ区切りリストはどうにも捉えようがない存在のようですが，プログラムの構成要素としてそういった型（厳密に言うと型ではないのでしょうが）があることを認識するとMATLABのコーディングがちょっとだけ楽しくなったりします．例えば，行ベクトルを作る時に，『スカラーをカンマで区切って大括弧で囲む』方法がありますが，これはまさに，『カンマ区切りリストを関数 horzcat に渡している』訳です．ですので，次の二つの文は，結果は同じでも全く違うことをしていることになります．

Code

[1 2 3 4 5]

Output

ans = 1x5    
     1     2     3     4     5

Code

[1,2,3,4,5]

Output

ans = 1x5    
     1     2     3     4     5

コンマ区切りリストが生まれる時

コンマ区切りリストは，プログラム中に明示的に書かれる場合以外にも，結構多くの場面で生まれています．上で説明した関数の返値の他に，セル配列や構造体配列を使っていると出くわしたりします．例えばセル配列

Code

a = {1,2,'a','b'};

この中身を取り出す時によくやるのが a{:} ですが，これをやると，結果がans = xxx の形で要素の数だけ出てきます．まさに，コンマ区切りリストが生まれているわけです．

Code

a{:}

Output

ans = 1
ans = 2
ans = 'a'
ans = 'b'

これを利用すると，関数への入力をセル配列にまとめて格納しておくことが出来ます．下の例は，関数 sum の引数 を一つのセル配列にまとめていて，関数に渡す時にコンマ区切りリストとして展開しています．実際は，このようにシンプルなケースではあまり使いませんが，関数への入力変数がやたらに多い場合には，コードもすっきりしますし，自作関数で「変数を構造体にまとめると後で展開するのが面倒くさい」という問題も起きないので重宝します．

Code

x = [1:9 nan 11:15]; 
nanFlag = 'omitnan';

varIn = {x,nanFlag};

sum(varIn{:})

Output

ans = 110

構造体配列を使っているときにも，コンマ区切りリストに遭遇することがよくあります．簡単な構造体配列を作ります．

Code

X(1:3) = struct("a",[],"b",[]);
for kk = 1:3
  X(kk).a = kk;
  X(kk).b = 2*kk;
end

ここで，フィールドの値を参照する時に配列の要素を指定しないと，コンマ区切りリストが生まれます．

Code

X.a

Output

ans = 1
ans = 2
ans = 3

このことに，上で少し触れた大括弧の使い方を応用すれば，構造体配列の特定のフィールドの値を取り出して配列に代入することが出来ます．これは，構造体を返す関数をループで回して結果を構造体配列に保存した場合に，その結果から特定のフィールドだけを取り出すのに便利です．（イマドキのMATLABユーザーなら struct2table を使うでしょ！という声もあるにはありますが・・・）

Code

[X.a]

Output

ans = 1x3    
     1     2     3

ちなみに，フィールドが行ベクトルの場合に上の表記を使うと想像していたのとはちょっと違う結果になります．

Code

X(1:3) = struct("a",[],"b",[]);
for kk = 1:3
  X(kk).a = [1 1 1]*kk;
  X(kk).b = [2 2 2]*kk;
end

コンマ区切りリストは出来ています．

Code

X.a

Output

ans = 1x3    
     1     1     1

ans = 1x3    
     2     2     2

ans = 1x3    
     3     3     3

でも，

Code

[X.a]

Output

ans = 1x9    
     1     1     1     2     2     2     3     3     3

この文脈では『大括弧でくくる』のが関数 horzcat の短縮形になっているので，行ベクトルが行の方向に連結されてしまっています．ですので代わりに vertcat を使えば，カンマ区切りリストに現れる行ベクトルを縦に連結した行列が得られます．（普通やりたいのはこっちの場合が圧倒的に多いですよね．）

Code

vertcat(X.a)

Output

ans = 3x3    
     1     1     1
     2     2     2
     3     3     3

カンマ区切りリストを便利に使う

上に書いたような，カンマ区切りリストの使い方がその威力を発揮するのが，cellfun や arrayfun といっしょに使用した場合です．cellfun や arrayfun は便利なのですが，対象とする関数の返値がスカラーでない場合には，必ずcell 配列で受けなければなりません（'UniformOutput' オプションを false に指定）．そのcell 配列の中身を取り出して，例えば行列に代入する際に，上で使った [a{:}] もしくは vertcat(a{:}) が使えます．（「カンマ区切りリストを使った！」という実感はないかもしれませんが・・・）

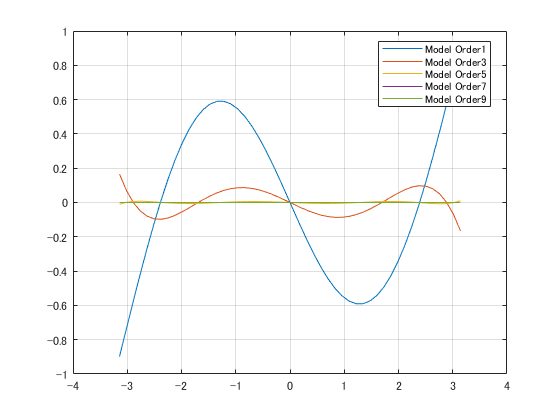
例として，サイン関数を奇数次の多項式でフィットして，残差をプロットします．

Code

t = linspace(-pi,pi,50)';
y0 = sin(t);

fitOrder = 1:2:9;
coefs = arrayfun(@(n) polyfit(t,y0,n), fitOrder,'UniformOutput',false);
yVals = cellfun(@(p) polyval(p,t), coefs,'UniformOutput',false)

	1	2	3	4	5
1	50x1 double	50x1 double	50x1 double	50x1 double	50x1 double

Code

yVals = [yVals{:}]

Output

yVals = 50x5    
   -0.8979    0.1649   -0.0102    0.0003   -0.0000
   -0.8613   -0.0587   -0.1266   -0.1281   -0.1279
   -0.8246   -0.2552   -0.2472   -0.2540   -0.2537
   -0.7880   -0.4258   -0.3678   -0.3754   -0.3753
   -0.7513   -0.5716   -0.4847   -0.4907   -0.4907
   -0.7147   -0.6937   -0.5948   -0.5979   -0.5981
   -0.6780   -0.7933   -0.6954   -0.6954   -0.6957
   -0.6414   -0.8715   -0.7843   -0.7816   -0.7818
   -0.6047   -0.9296   -0.8597   -0.8550   -0.8551
   -0.5681   -0.9686   -0.9202   -0.9144   -0.9144

Code

plot(t,yVals-y0,'-');
legend("Model Order"+string(fitOrder),'Location','best');
grid on;

おわりに

ここで紹介している例を含め，コンマ区切りリストについての詳細な解説が，MATLABドキュメンテーションに掲載されています．（ドキュメンテーションのホームからたどり着くパスが見当たらないので，ローカルバージョンのドキュメンテーションを参照されている方は，検索窓に「コンマ」と入力して検索してみてください．）この機会に是非ご一読を．MATLABの世界が広がりますよ．