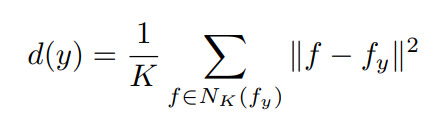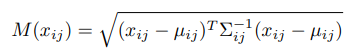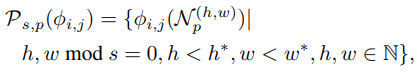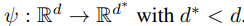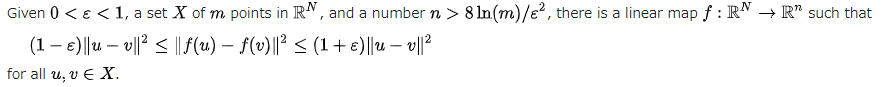概要
- SPADE~PaDiM~PatchCoreに関連するリンクとメモです。
- 2021/09/05 まとめて試せるレポジトリの紹介を追加しました。
- 2021/10/09 Gaussian AD の日本語解説記事があったのでリンクを追加。
- 2021/10/26 PatchCoreの処理の流れについて追記しました。
- 2022/06/07 PatchCoreの公式実装公開とスコアの更新について追記しました。→ リンク
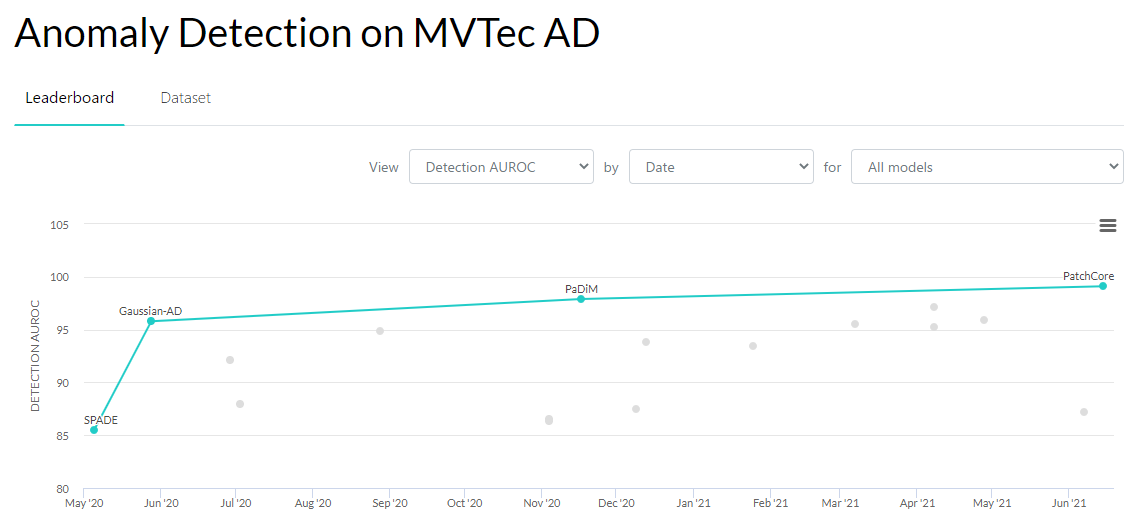
この1年の流れ
- この欠陥の検出をニューラルネットワークの再学習なしでしています。しかもSOTA。
- 最近までAutoEncoderが強かったです。
- 2020/05にSPADEが登場しました。
- その後にSOTAを更新しているのはSPADEの派生です。
- Image-levelの精度は99.1%までいってしまいました。
評価に使うデータ MVTec AD
マシンビジョン業界で有名なHALCONの会社であるMVTECが作ったデータベースです。
2019/06にCVPRで発表。
- 15のカテゴリー
- 5354枚の画像
- 70種類の欠陥と対応したマスク
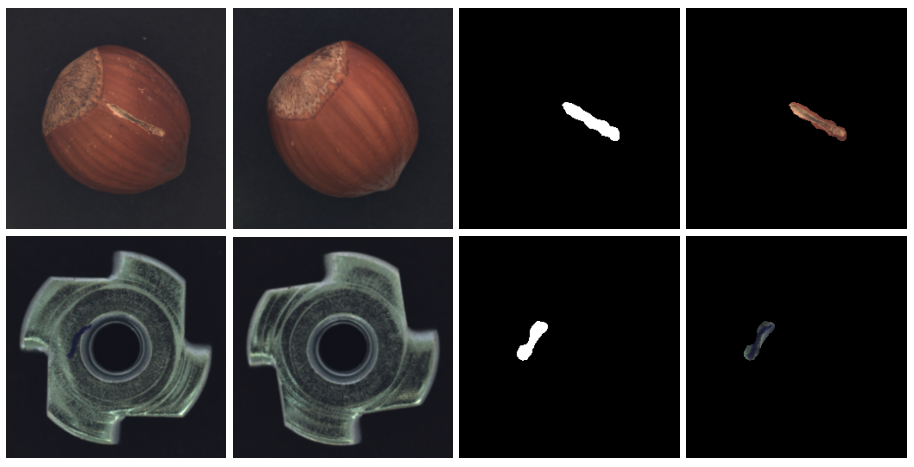
せっかくなので、一例をちょっと細かく紹介します。
画像は、15カテゴリー中の一つ「cable(線を剥いてある3芯のケーブル)」のテスト画像です。
70種類の欠陥のうち8種類の欠陥が「cable」で発生します。
それらの欠陥のひとつ「bent_wire(銅線が折れている)」が発生している画像です。

折れた銅線の画素を白く塗ったマスク画像が用意されています。

良品の画像が手に入りやすい現実を表していて、このパターンの画像はこれが全部と数は少ないです。
cableの良品テスト画像は58枚。トレーニング画像(良品のみ)は224枚。
他もこういう調子で分類されています。
データは「こちら」からダウンロードできる。1時間くらいかかりました。
評価指標 ROCAUC/AUROC
論文によって2つの呼び方をしていますが、意味はどちらも同じです。
①ROC area under the curve (ROCAUC)
②the Area Under the Receiver Operating Characteristic curve (AUROC)
こちらの説明が分かりやすいです。しかも小テスト付き。
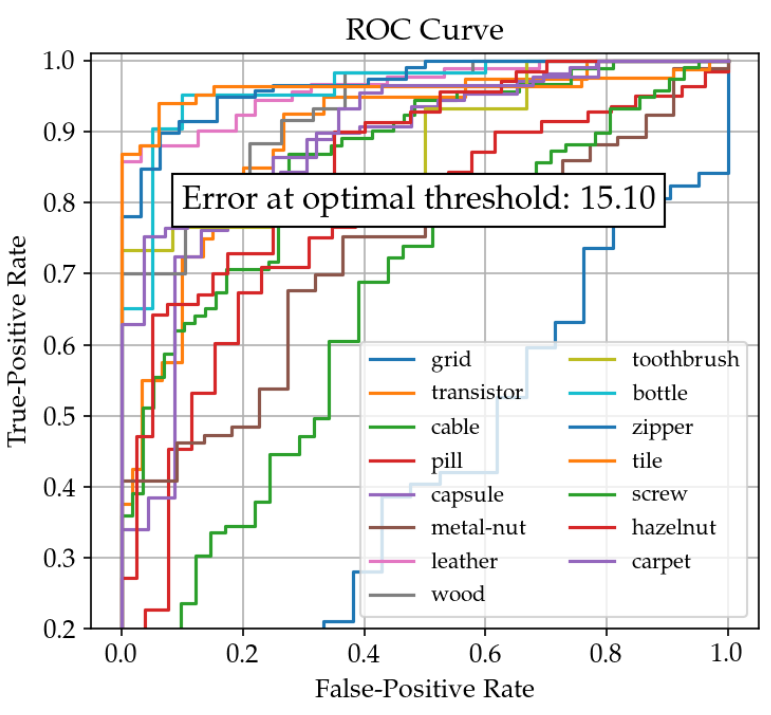
今回の問題での例で説明します。PatchCoreの論文に載っているSPADEのROC Curveがこちらです。
グラフの説明
1)異常検知の閾値を変えながらプロットします。
2)縦軸がTure-Positive Rate(検知できた異常画像の数を異常画像全体で割ったもの)
3)横軸がFalse-Positive Rate(誤検知した正常画像(偽陽性)の数を正常画像全体で割ったもの)
4)とても感度が高い(許容する範囲が広い)設定にすると、すべて陽性になってグラフの右上(1,1)に到達します。
5)とても感度が低い(許容する範囲が狭い)設定にすると、陽性になるものが全然なくて、グラフの左下(0,0)に到達します。
6)あとはその間をプロットしています。ランダムなとき(0,0)と(1,1)を結ぶ直線です。青い「grid」の線は間違えすぎてやばい状態です。
すごく上手くいくと下のグラフのようになります。PatchCoreのグラフです。
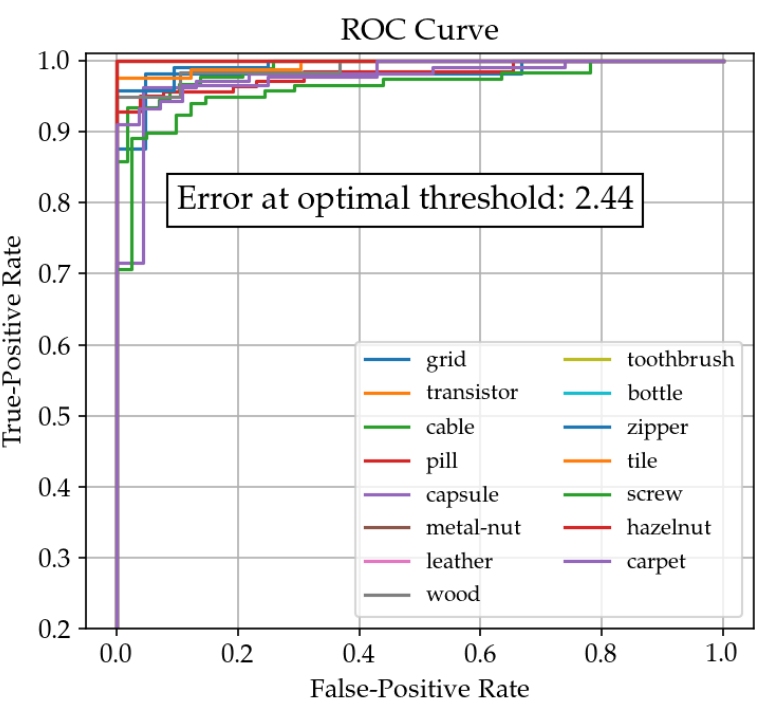
そしてこのグラフの下側の面積(≦ 100%)がAUROCです。最初の偽陽性が出るまで感度を高めたときに全てのTure-Positiveが出れば100%です。
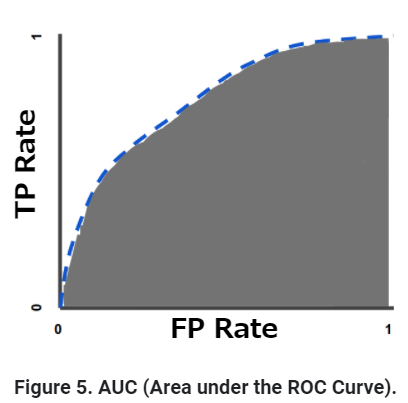
画像単位で比率をだしていましたが、画素単位での比較もあります。
画像単位のほうをimage-levelと呼んでいます。
Deep Nearest Neighbor Anomaly Detection [2020/02]
必ず引用されているのがLiron Bergman, Niv Cohen, Yedid Hoshen の3人の論文。
- 「画像」単位の異常検知
- ImageNetで訓練したResNetを利用する(再訓練なし)
- 正常な画像$y$を変換した特徴量$f_y$を保持する
- 推論では入力した画像の特徴量$f$と$f_y$のk-Nearest Neighbor distanceで判定
確かにこの方式の原点ですね。
ただし、異常個所を表すセグメンテーションの表示はまだ出てきません。
SPADE: Sub-Image Anomaly Detection with Deep Pyramid Correspondences [2020/05]
SPADEは上の論文からBergmanを除いた二人です。
異常個所を表示する拡張をしてSPADEになりました。

- 画素」単位の異常検知 → 異常個所の表示
- ImageNetで訓練したResNetを利用する(再訓練なし)
- 正常な画像$y$の各画素$p$を変換した特徴量$F(y,p)$を保持する
- 推論では入力した画像の画素の特徴量$f$と$F(y,p)$のk-Nearest Neighbor distanceで判定
- 解像度と深い特徴抽出を両立するために、feature pyramidの各層をconcatする
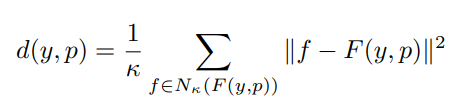
メモ
- 評価基準としてMVTec ADデータセットとROCAUCが登場。PROとか短縮したのが分からなくなたらこの論文を見る。
- 入力画像:224x224。出力は1~3ブロック目(56x56,28x28,14x14)の最終層を同じ重みで結合。
- 画素ごとのスコアはガウシアンフィルタ($\sigma=4$)でスムージング。
公式実装はみつかりませんでした。↓は非公式ですが検出例やグラフが充実しています。
Gaussian AD [2020/05]
この論文はICPR2020。読めてないです。
これだけ公式実装があった。
2021/10/09追加:日本語解説。なぜ2021/9/10にこれを選んだのだろう?と思いましたが、参考になる内容でした。
PaDiM: a Patch Distribution Modeling Framework for Anomaly Detection and Localization [2020/11]
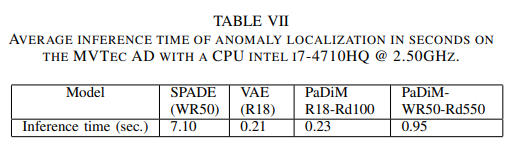
SPADEは画素ごとにkNNで距離を出すので推論が遅いです。
それを克服するために正常な画像のデータを統計量にしておくというアイデアで高速化しました。
性能もこの時点でのSOTAです。
速くなるのはわかるですが、SPADEと比べて性能が一気に上がる理由がよくわかりません。誰か教えてください。
- 「画素」単位の異常検知 → 異常個所の表示
- ImageNetで訓練したResNetを利用する(再訓練なし)
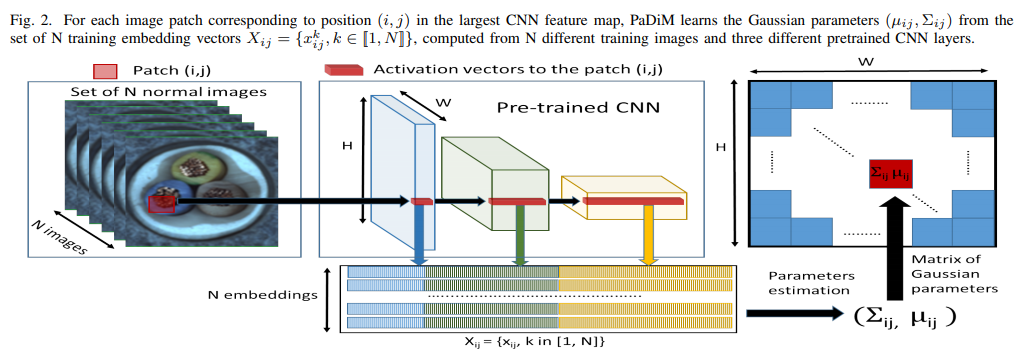
- 正常な画像$y$の各画素$p$を変換した特徴量の平均$\mu_{i_j}$ と共分散行列$\Sigma_{ij}$を保持する
- 推論では入力した画像の画素の特徴量$f$とのマハラノビス距離で判定する
- 解像度と深い特徴抽出を両立するために、feature pyramidの各層をconcatする
- 高速化のために特徴量を削減している。PCAよりランダムサンプリングのほうが性能が良かった。
マハラノビス距離についてはこちらの説明を参照してください。
やはり非公式実装。
PaDiMの日本語解説。
PatchCore: Towards Total Recall in Industrial Anomaly Detection [2021/06]
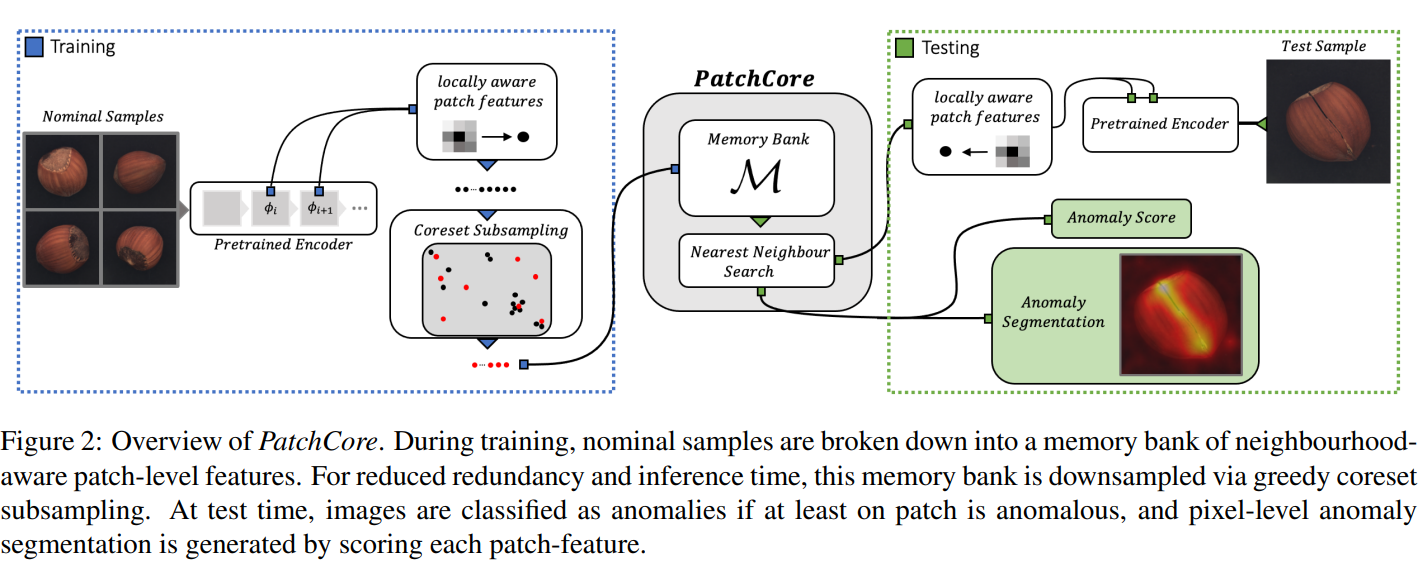
PaDiMとは違った方法で高速化しています。具体的には正常画像を効率的に間引いたサンプルをPatchCoreと呼ばれるモジュールに保持しています。
- Image-levelのAUROCスコア99.1%。データを1%まで間引いてもスコアは99.0%。
- このときのエラーの閾値も従来より低い。
- cold-startという言葉を好んで使っている。one-class classificationを指すとの説明付きだがニュアンスがよくわからない。
非公式実装が早くも2つ。
(2022/6/7追記) 2022/5/6にPatchCoreの公式実装が出ました。
このタイミングで論文にも変更がありスコアが上がっています。
Image-levelのAUROCスコアが99.1% → 99.6%。
以下が差分です。
・backboneをWide ResNet 50 から 101 に変更。
・画像サイズを(224 x 224)から(320 x 320)に変更。
・加えてDenseNet201とResNext101をアンサンブル。
・データのサンプリングは100%から1%に下げて速度を確保。
Wide ResNet 50と画像サイズ(224 x 224)は事前学習済みのネットワークを使った先行研究に合わせたものでした。
fastflow(更新直前までのSOTAでnormalizing flowを利用)など別方式の後続の論文に対抗して縛りを緩めたのだと思われます。
PatchCoreの処理内容 (2021/10/26追記)
処理の流れ
-
wide resnet50 の中で2ブロック目(28x28)と3ブロック目(14x14)の出力を使う
-
位置に敏感にならないように周囲の特徴量と合わせる。下みたいに書いてるが、実際には単に3x3のglobal average pooling。平均化のサイズ$p = 3$,
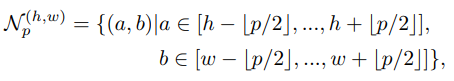
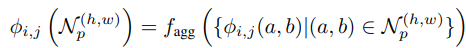
-
二つのブロックの対応する特徴量をconcatする。方法はPaDiMと同じ。小さいほうをバイリニアで大きくして結合。結局28x28のmapに対応した特徴量になる。
-
サンプル数を減らす高速化。貪欲法(サブサンプルの2個目からは今までの選択要素から最も遠いものを選択)で$l$個のサンプルを決める。サブサンプルの個数$l$ はデータに対する比率(1%~)で決める。

補足事項
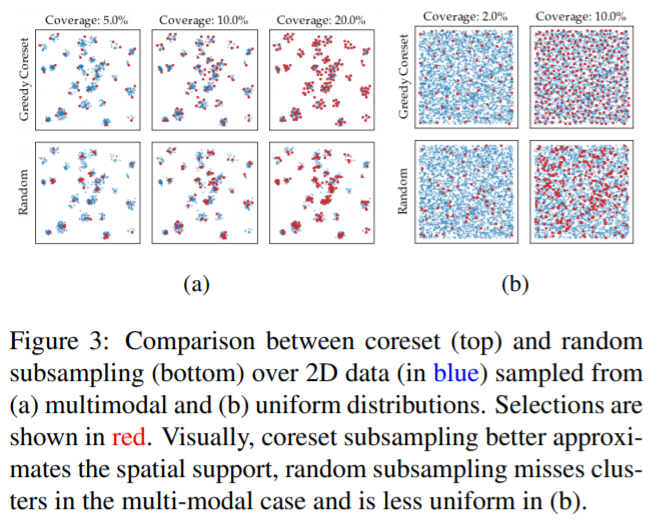
ランダムサンプリング
Johnson–Lindenstrauss の補題が根拠。
サンプルの数mに対して削減後の次元nが大きければ、ランダムサンプリングが結構高い確率でサンプル同士の距離を再現するといっている。
証明はこれがとても丁寧。
http://dopal.cs.uec.ac.jp/okamotoy/lect/2010/metemb/ho4.pdf
以上の背景から以下を使っています。
貪欲法で正しくサンプルを選べる?
-
k個のサブサンプルで近似したいので、他の全部の点がサブサンプルした点から離れないようにしたいです。このような問題をk-center 問題といいます。
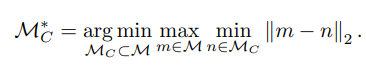
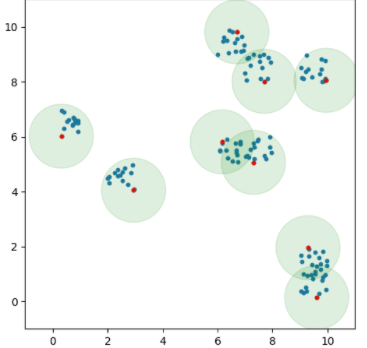
-
k-centerはNP困難なのだそうです。最適解は諦めて貪欲法で近似します。
- サブサンプルの2個目からは今までの選択要素から最も遠いものを選択していきます。
-
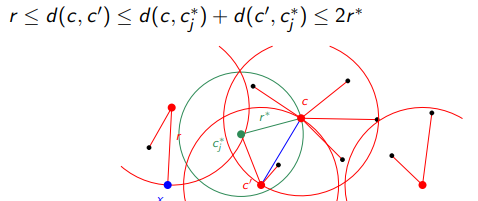
得られた解は最適解の距離の2倍以内(2近似解)に抑えられます。
イラストはこちらから引用しました。
2近似解になることについて日本語の証明。ありがたいです。
コード
まとめて試せるレポジトリの紹介 (2021/09/05追記)
SPADE, PaDiM, PatchCoreをまとめて実装しているレポジトリがありました。ありがたい。
streamlitによるwebアプリが実装されており、手元の写真による評価が簡単です。
↓雑誌の文字と同じ色のペンが乗ってもちゃんと反応していました。

ただし、ヒートマップの表示は要注意です。色の割り当てを画像1枚ごとに決めています。
なので、正常な画像でもまだら模様を作ってしまいます。

対策してみた
streamlit_app.pyを改造して固定にしてしまうのが楽そうです。

しかし、適切な値がモデルと画像ごとに違う。。。GUIを足してみました。緑で囲っている部分です。
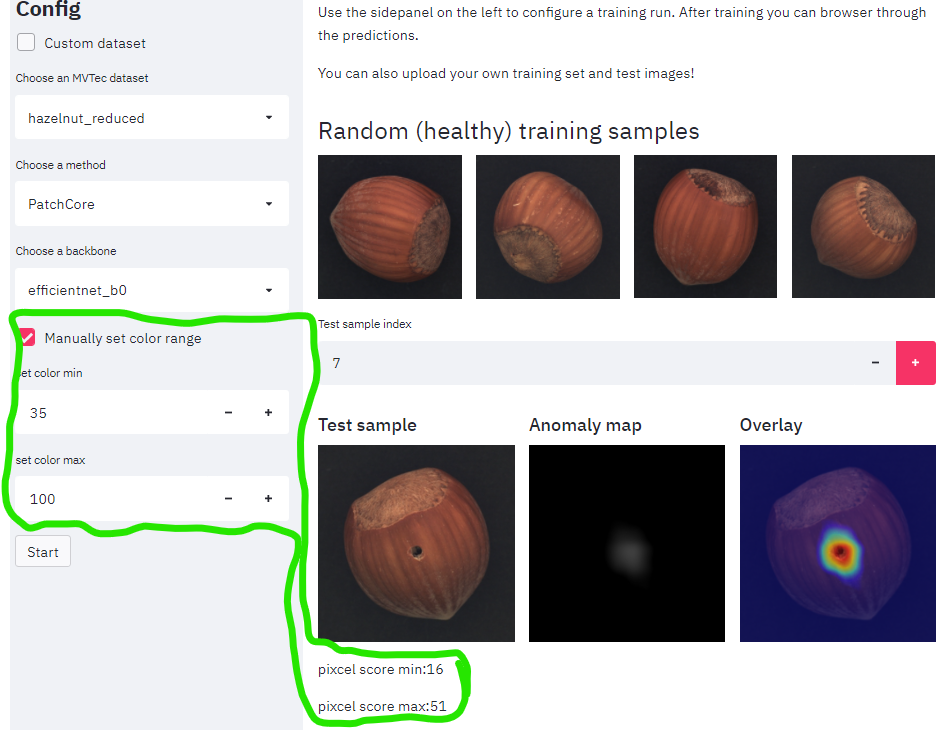
↓改造を入れたレポジトリです。 本家にマージしてもらいました。