概要
- ディープラーニングの話を聞いていて、なんか物理っぽいんだけどなんだったっけという内容のメモです。
- どれも確率を扱う学問なので当たり前なのかなとも思いますが、知ってることと結びつくとイメージわきます。
- 気づくたびに書き足していきます。
- こういうのもあるよと教えてもらえるとすごい嬉しいです。
- 「いいね❤」もらえるとやる気出ます！
20210919: 初稿。エントロピー、温度付きSoftMax、Relu。
20211003: シグモイド、ヒルベルト空間、L2。
20211113: ベクトル、テンソル。
エントロピー
-
シャノンエントロピー（情報理論）
-
ギブスエントロピー（統計力学）
-
フォンノイマンエントロピー（量子力学）
温度付きSoftMaxとボルツマン分布
-
温度付きSoftMax（機械学習）
-
ボルツマン分布（統計力学）
温度によるエネルギー分布の違い。平均値はあがり、分布は広がっている。図はこちらの記事より引用。
シグモイド
ハイパボリックタンジェント $\text{tanh}(x)$とは顔なじみのつもりでいましたが、
実は$\text{cosh}(x)$ 、$\text{sinh}(x)$に比べると物理での出現率が低い？
- シグモイド（機械学習）
- イジングモデルの平均場近似（統計力学）
- フェルミ分布（量子統計力学）
- こんな洒落た書き方したい。
ヒルベルト空間
- SVMのカーネルトリックの再生核ヒルベルト空間（機械学習）
- ブラケットや波動関数（量子力学）
L2ノルム
- L2正則化（機械学習）
損失関数${\displaystyle E({\boldsymbol {w}})} $を書き換える。
L2正則化のときはルートをつけずにノルムの二乗なので、この項をL2ノルムと言われると違和感がある。ちなみに正則化はregularization。
- 正規化（量子力学）
L2ノルム（つまりその2乗も）が１になるように正規化(normalization)するのが普通。
変分法
物理の世界だと保存則にかかわるので超重要。
- Normalizing Flow（機械学習）
- ネーターの定理（量子力学）
アインシュタインの縮約
-
einsum（機械学習）
pytorchのやつ -
計量を使った計算（量子力学）
-
完全反対称テンソルを使った計算（量子力学）
ベクトル
プログラミングの世界以外では配列とベクトルは違うものです。
あとから名前を付けておいて意味が違うstd::vectorは罪深いと思う。
- std::vector (c++)
1次元の動的配列（コンテナ）として表現されるデータ構造。
std::vector<int> v = {1, 99, 4};
-
ベクトル (数学、物理)
ベクトル空間の元。線形性を持つ、すなわち和とスカラー倍を取る事ができる量。
一階のテンソル。
向きを持った量。速度とか力とか量自体は座標系に寄らないので、座標系を変えると表現（数字の組み合わせ）が変わる。
テンソル
プログラミングの世界以外では行列とテンソルは違うものです。
あとから名前を付けておいて意味が違うTensorFlowは罪深いと思う。
-
tf.Tensor, torch.Tensor (ディープラーニング)
行列。多次元の数字のコンテナ。
-
テンソル、テンソル場 (数学、物理)
ベクトルを一般化した量。基底を決めると行列で表現できる。
慣性モーメントとかエネルギー運動量テンソルとか、量自体は座標系に寄らないので座標系を変えると表現（数字の組み合わせ）が変わる。
（大雑把すぎる説明）
座標系を変えたとき、n階のテンソルの表現はベクトルの表現を変える操作n回分で変換できる。
2階のテンソルだったらこのような感じ。
こちらの動画がおすすめ。
あとこれも分かりやすい。
参考
https://www.tensorflow.org/api_docs/python/tf/Tensor
https://pytorch.org/docs/stable/tensors.html
https://ja.wikipedia.org/wiki/%E3%83%86%E3%83%B3%E3%82%BD%E3%83%AB
名前だけ違う系
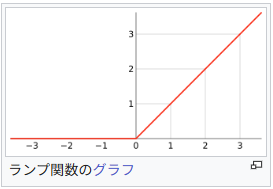
- ReLU と ランプ関数
参考
まだ読んでないがきっと参考になる。