概要

ベイズ推論による機械学習入門の内容について、実際にpythonで試してみた際の記録です。

ポアソン混合モデルをガウスサンプリングを使って推論する箇所について記載しました。

実施内容

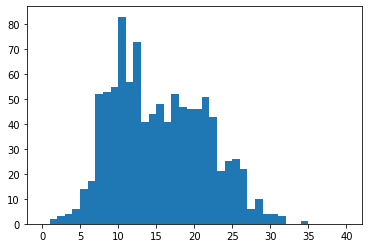
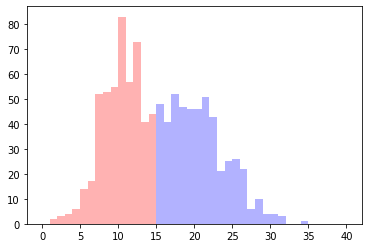
以下のように作成したデータから、ポアソン混合モデルの事後分布を推論します。

import numpy as np
import matplotlib.pyplot as plt

np.random.normal(0, 1, 10)
poi_test = np.random.poisson([10, 20],(1000,2))
s_test = np.random.multinomial(1, [0.5,0.5], (1000))
x = np.prod(np.power(poi_test, s_test), axis=1)
plt.hist(x,bins=40, range=(0,40))

ポアソン混合モデルから出力したデータから、ポアソン混合モデルの事後分布を推論するのであまり面白くはないですけどねw

ポアソン混合モデルのガウスサンプリング

ポアソン混合モデルのガウスサンプリングは以下のようになります。

sのサンプリング

s_n \sim Cat(s_n|\eta_n) \\
\eta_{n,k} \propto exp\{x_n\ln\lambda_k-\lambda_k + \ln\pi_k\} \\
\left( s.t. \sum_{k=1}^K\eta_{n,k}=1\right)

# sのサンプリング
def sample_s(x, lam, pi):
  s = []

  for n in range(len(x)):
    eta_n = np.exp( x[n] * np.log(lam) - lam + np.log(pi))
    eta_n = eta_n / np.sum(eta_n)
    s_n = np.random.multinomial(1, eta_n)
    s.append(s_n)
  s = np.array(s)
  return s

λのサンプリング

\lambda \sim Gam(\lambda_k|\hat{a}_k, \hat{b}_k) \\
\hat{a}_k = \sum_{n=1}^Ns_{n,k}x_n + a \\
\hat{b}_k = \sum_{n=1}^Ns_{n,k} + b

# lambdaをサンプリング
def sample_lam(x, s):
  a_hat = []
  b_hat = []
  for i in range(2):
    a_hat_k = np.sum(s[:, i] * x, axis=0) + a
    b_hat_k = np.sum(s[:, i], axis=0)
    a_hat.append(a_hat_k)
    b_hat.append(b_hat_k)
  lam = np.random.gamma(np.array(a_hat), 1/np.array(b_hat))
  return lam

πのサンプリング

\pi \sim Dir(\pi|\hat{\alpha}) \\
\hat{\alpha}_k = \sum_{n=1}^Ns_{n,k} + \alpha_k

# piをサンプリング
def sample_pi(s):
  alpha_hat = np.sum(s, axis=0) + alpha
  pi = np.random.dirichlet(alpha_hat)
  return pi

サンプリングの実行

# 初期値
a = 2
b = 2
alpha = np.ones((2))
lam = np.random.gamma(a,b,2)
pi = np.random.dirichlet(alpha)

s_samples=[]
lam_samples=[]
pi_samples=[]
for i in range(5):
  print(i)
  for j in range(100):
    s = sample_s(x, lam, pi)
    s_samples.append(s)

    lam = sample_lam(x, s, a, b)
    lam_samples.append(lam)
    pi = sample_pi(s, alpha)
    pi_samples.append(pi)

サンプルした値をみる

本にはサンプル方法は書かれていたのですが、サンプルしたものをどうすればいいのかは良くわかりませんでした（理解度の問題かもしれませんが）。
そこで色々グラフ化してみます。

サンプルされた値からクラスを決めてみる

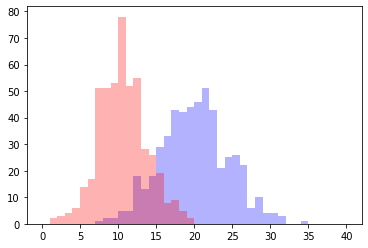
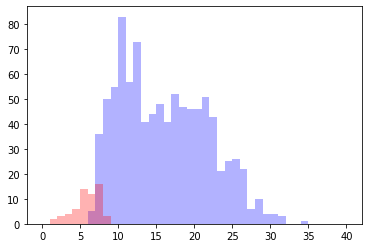
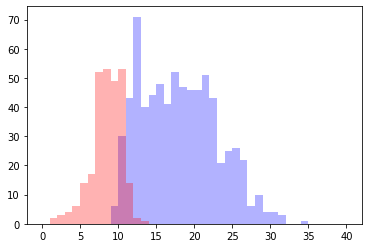
だいぶ雑ですが、クラス毎にサンプルされた値を全て足して、大きい方にクラス分けします。こういう方法で分けるのが正しいのかはわかりません。。。

x_1 = []
x_2 = []
tmp = np.sum(np.array(s_samples),axis=0)
for i in range(len(x)):
  if tmp[i][0] > tmp[i][1] :
    x_1.append(x[i])
  else:
    x_2.append(x[i])

正解のデータはこんな感じ

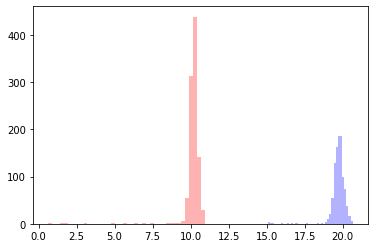
10回サンプルした場合

10回くらいだとあまりいい感じに別れませんね。

20回サンプルした場合

1000回サンプルした場合

なんだか思いの外バツっと別れました。

lambdaの分布をみてみる

これは最初に決めた10,20あたりにピークが来ました。ちゃんと推論できたってことでいいのかな？

ポアソン混合モデルを使ったクラスタリング

概要