#PowerApps における数学 (アニメーション)

はじめに

PowerAppsで作成するアプリのUIを、ネイティブアプリまたは通常のWebアプリに近づける１つの方法として、アニメーションの効果を工夫するということがあります。
例えば、サイドメニューを表示する際、単純に考えれば、タイマーの時間に比例したX座標をサイドメニューに設定するでしょう。

Object.X : -1*Object.Width + Object.Width*Timer1.Value/Timer1.Duration

もちろんこれでもタイマーコントロール(Timer1)の時間がTimer1.Durationになったときに、メニューが表示されます。ですが、メニューは、単調な速度で移動して急に静止するので、非常に不自然な動きになります。
これを解消し、メニューの動きをより自然にするために、私はしばしばHyperbolic Tangent関数で挙動を制御しています。※Hyperbolic Tangent関数の概形は下図を参照してください。

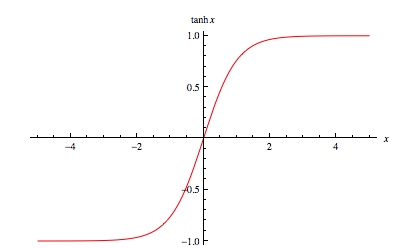
Hyperbolic Tangent関数は、おおよそ、x=-3のときTanh(x)≒-1になり,x=3のときTanh(x)≒+1の値をとります。また、最初(xが小さい時)はxの増加に対して急激に値が大きくなるのに対して、x=2付近からサチュレートし、１に漸近することが見て取れます。
本投稿では、このHyperbolic Tangent関数を利用して、PowerAppsにおけるアニメーション効果をいかに実現するか、改善するかを説明します。

サイドメニューの例

先ほどのサイドメニューの改善例を示します。まずはタイマーの時間に比例した場合の動作と、Hyperbolic Tangentを導入した場合の動作を見てみましょう。

Another example for animation: Show/Hide side menu pic.twitter.com/6nNjc9wFTH

— Hiro (@mofumofu_dance) September 30, 2019

右側がHyperbolic Tangent関数を利用した場合です。
動作の開始からすぐに早いスピードで動かしたい場合には、単純に以下のようにXを設定します。

Object.X : -1*Object.Width + Object.Width*(( Exp(2*3*Timer1.Value/Timer1.Duration) -1 )/( Exp(2*3*Timer1.Value/Timer1.Duration) +1 ))

ちょうど、以下の置き換えをおこなったようになっています。

Timer1.Value/Timer1.Duration　→ (( Exp(2*3*Timer1.Value/Timer1.Duration) -1 )/( Exp(2*3*Timer1.Value/Timer1.Duration) +1 ))

この置き換えがほとんど全てです。右側の関数は 0->1に変化するので、これを利用することによって、あらゆる動作（移動、回転、色の濃淡の変更）を、タイマーの時刻に比例した動作よりも自然に表現することができます。

より一般的には以下のようにかけます。

Object.X : [target x position]-1*[move distance] + [move distance]*(( Exp(2*3*Timer1.Value/Timer1.Duration) -1 )/( Exp(2*3*Timer1.Value/Timer1.Duration) +1 ))

ここで"[target x position]"は、最終的にオブジェクトを配置したいX座標で、"[move distance]"は動く幅になります。即ち、初期位置は"[target x position] - [move distance]"で与えられます。

ちなみに戻す場合には

Object.X : [target x position]-1*[move distance]*(( Exp(2*3*Timer1.Value/Timer1.Duration) -1 )/( Exp(2*3*Timer1.Value/Timer1.Duration) +1 ))

と記述します。
出る/戻るのステート管理はなんらかの変数で行ってください。

円運動の例

あまり利用シーンはありませんが、ローディングサークルのようなアニメーションでも、Hyperbolic Tangentは有効です。

#PowerApps animation
Heyperbolic tangent is very useful for most of animation.
This is example for circular motion. pic.twitter.com/BSdnH7w3cr

— Hiro (@mofumofu_dance) September 30, 2019

この場合には、最初に動き出す円と、あとから動き出す円の角度成分（極座標におけるθ）にHyperbolic Tangentを適用しています。サイドメニューの例との違いは、円が最初はゆっくり動き出し、加速し、最後に静止するということです。
これを実現するためには、以下のような置き換えを行います。

Timer1.Value/Timer1.Duration　→ (( Exp(4*3*(Timer1.Value/Timer1.Duration-0.5)) -1 )/( Exp(4*3*(Timer1.Value/Timer1.Duration-0.5)) +1 ) +1)/2

先ほどとの違いは何かというと、"(....+1)/2"の部分です。Hyperbolic Tangentは、xが負の場合に-1になります。これを0->1の変化に直すために、１を足して２で割っています。
また、Exp()の中身も、タイマーの時刻が0の場合に、負の値を取るようにずらしています。

このような置き換えを円運動の角度部分に施すことによって、通常見るようなWebのローディングサークルと同様のアニメーション効果を実現できます。

おわりに

今回のアニメーションを含むサンプルアプリは以下のURLで公開されています。実際に数式をみてみて、自分のアプリに適用してみてください！
すごくそれっぽくなります！