本稿は計算化学等で周期境界条件を用いた計算を行っている方向けのメモです。
並進ベクトル(Translation Vectors: TV)の長さと角度が既知であるユニットセルについて、格子点の3次元座標(TVの成分)を求める計算について述べます。結晶構造データベースから取得したCIFファイルに記載された結晶構造をxyzに変換するなどの際にご参照頂ければ幸いです。
結晶単位格子
AO系の結晶格子の一例を示します。
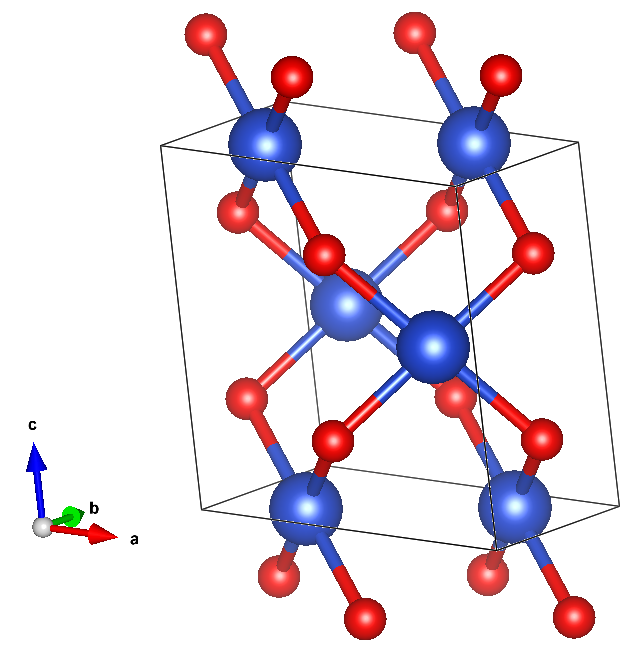
このような単位結晶格子は通常、$a$軸、$b$軸、$c$軸という3次元のベクトルによって記述されます。
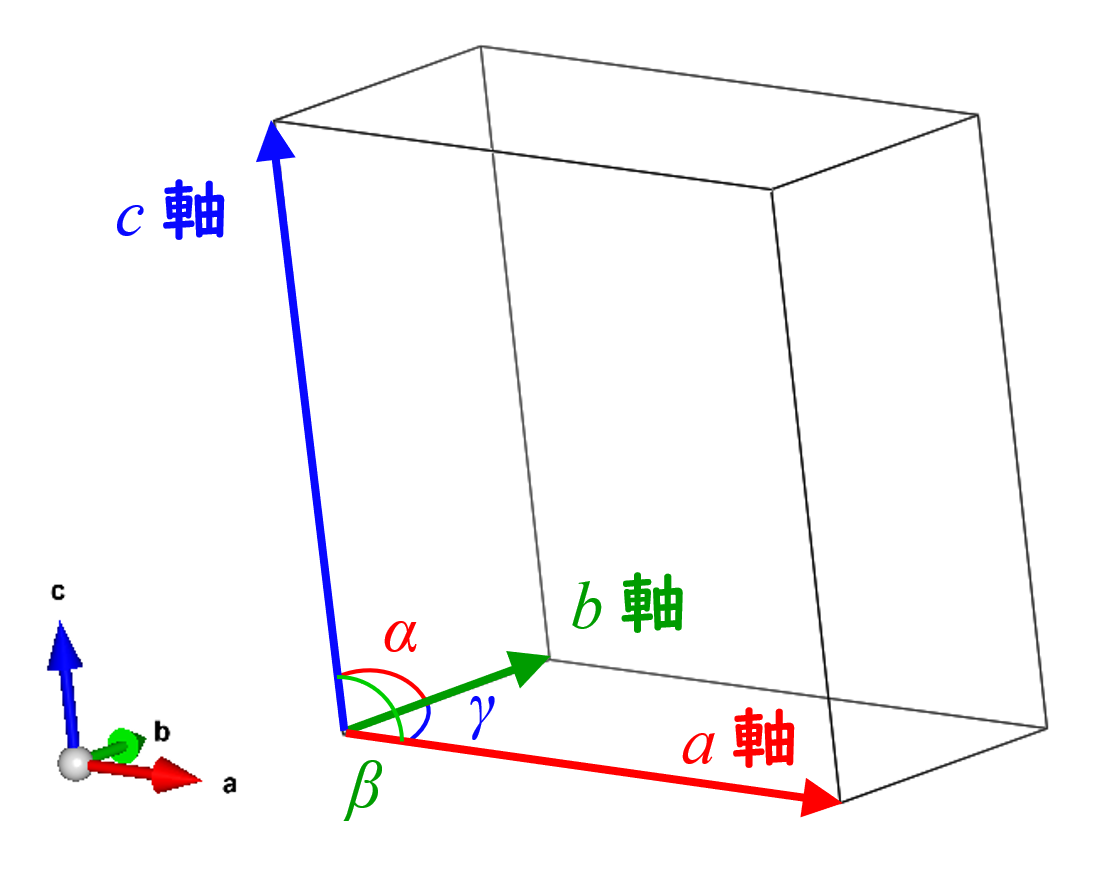
$b$軸と$c$軸の成す角が$\alpha$、$c$軸と$a$軸の成す角が$\beta$、$a$軸と$b$軸の成す角が$\gamma$です。
軸の長さとそれらの角度が分かっていれば3次元のカーテシアン座標系(直交座標系)に変換することが可能です。
カーテシアンへの変換
結晶格子を変換後の座標は一意に定まりません。
ここでは$a$軸を$x$軸に合わせて、$b$軸を$xy$平面に乗せるように変換します。
結果だけ載せると、
\vec{a}=\left[\begin{array}{c}
|\vec{a}| \\
0 \\
0
\end{array}\right]
\vec{b}=\left[\begin{array}{c}
|\vec{b}| \cos \gamma \\
|\vec{b}| \sin \gamma \\
0
\end{array}\right]
\vec{c}=\left[\begin{array}{c}
|\vec{c}| \cos \beta \\
\dfrac{|\vec{c}|(\cos \alpha -\cos \beta \cos \gamma )}{\sin\gamma } \\
|\vec{c}|\sqrt{1-\cos^2 \beta-\left(\dfrac{\cos \alpha -\cos \beta \cos \gamma}{\sin\gamma }\right)^2}
\end{array}\right]
となります。軸はすべて原点を始点としています。
因みにセルの体積$V$は$$V=|\vec{a}||\vec{b}||\vec{c}|\sqrt{\sin^2 \beta\sin^2 \gamma-\left(\cos \alpha -\cos \beta \cos \gamma\right)^2}$$で求められます。$V=\left|\vec{a} \cdot \vec{b} \times \vec{c}\right|$ としても求められますが、いまTVは
\small \left[\begin{array}{ccc}
|\vec{a}| & 0 & 0 \\
|\vec{b}| \cos \gamma & |\vec{b}| \sin \gamma & 0 \\
|\vec{c}| \cos \beta & \dfrac{|\vec{c}|(\cos \alpha -\cos \beta \cos \gamma )}{\sin\gamma } & |\vec{c}|\sqrt{1-\cos^2 \beta-\left(\dfrac{\cos \alpha -\cos \beta \cos \gamma}{\sin\gamma }\right)^2}
\end{array}\right]
という下三角行列になるように整理されているので、セルの体積は対角成分の積で表せます。
変換用コード
変換用のpythonのスクリプトを載せておきます。リスト内の数値は適当に書き換えて下さい。
なお、pythonでは三角関数の中身をラジアン単位にする必要があるので、$\pi/180$ を乗じて換算する必要があります。
import math
length = [6.18704, 2.91581, 7.28313] # a, b, c
degree_angle = [81.6066, 99.4557, 76.4221] # alpha, beta, gamma
angle = [i * math.pi/180.0 for i in degree_angle] # degree --> rad
a_axis = [0.0] * 3
b_axis = [0.0] * 3
c_axis = [0.0] * 3
a_axis[0] = length[0]
a_axis[1] = 0.00000
a_axis[2] = 0.00000
b_axis[0] = length[1]*math.cos(angle[2])
b_axis[1] = length[1]*math.sin(angle[2])
b_axis[2] = 0.00000
c_axis[0] = length[2]*math.cos(angle[1])
c_axis[1] = length[2]*(math.cos(angle[0])-math.cos(angle[1]) * math.cos(angle[2]))/math.sin(angle[2])
c_axis[2] = length[2]*math.sqrt(1-math.cos(angle[1])**2-((math.cos(angle[0])-math.cos(angle[1])*math.cos(angle[2]))/math.sin(angle[2]))**2)
print("TV",'{:>14.10f}'.format(a_axis[0]),'{:>14.10f}'.format(a_axis[1]),'{:>14.10f}'.format(a_axis[2]))
print("TV",'{:>14.10f}'.format(b_axis[0]),'{:>14.10f}'.format(b_axis[1]),'{:>14.10f}'.format(b_axis[2]))
print("TV",'{:>14.10f}'.format(c_axis[0]),'{:>14.10f}'.format(c_axis[1]),'{:>14.10f}'.format(c_axis[2]))