はじめに
numpyの多次元配列の次元を落としたり,任意の2つの一元配列を取り出して分散図を書く練習をします.
ここではサイズ2×3×4の3次元の配列を題材とします.
インデックスはdata[z][y][x]のように,zからx方向に並びます.zは最大1,yは最大2,xは最大3となります.本記事における配列の図はすべて,奥行きをz,下方向yを,右方向をxとしています.

練習
練習1 題材となる3次元配列の生成
問題
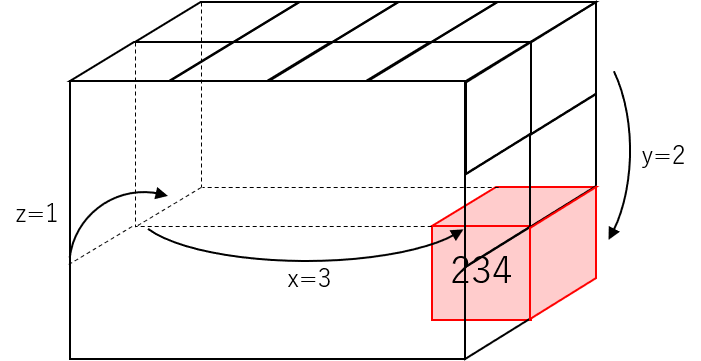
以下の図のようにdata[z][y][x]=(z+1)100+(y10)+(z+1)という値が設定されている3次元配列を生成してください.

解答例
3重ループ文で書く場合
q0.py
>>> data=np.zeros((2,3,4),dtype=np.int)
>>> for x in range(4):
... for y in range(3):
... for z in range(2):
... data[z][y][x]=(z+1)*100+(y+1)*10+x+1
内包表記でも書けます
q1.py
>>> import numpy as np
>>> data=np.array([[[(z+1)*100+(y+1)*10+x+1 for x in range(4)] for y in range(3)] for z in range(2)])
>>> data
array([[[111, 112, 113, 114],
[121, 122, 123, 124],
[131, 132, 133, 134]],
[[211, 212, 213, 214],
[221, 222, 223, 224],
[231, 232, 233, 234]]])
>>> data[1,2,3]
234
練習2 1次元配列(ベクトル)の取り出し
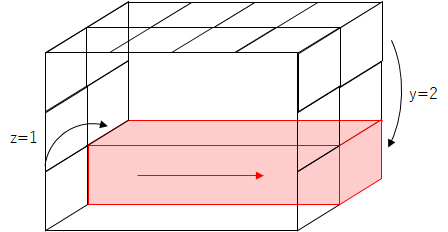
問題2-1 赤色部分のデータを1元配列として取り出してください
 ### 解答例2-1
```python:q2-1.py
>>> data[1,2,:]
array([231, 232, 233, 234])
# 省略形
>>> data[1,2]
array([231, 232, 233, 234])
```
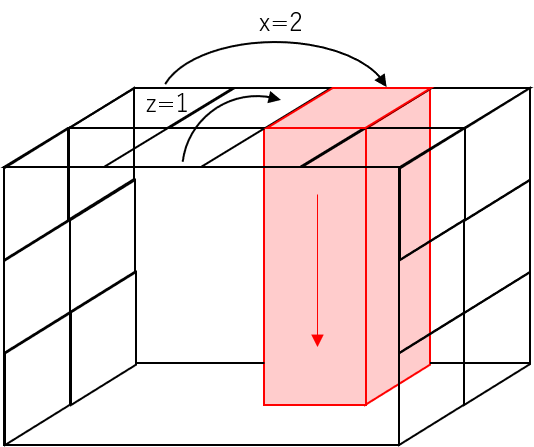
### 問題2-2 赤色部分のデータを1元配列として取り出してください
### 解答例2-1
```python:q2-1.py
>>> data[1,2,:]
array([231, 232, 233, 234])
# 省略形
>>> data[1,2]
array([231, 232, 233, 234])
```
### 問題2-2 赤色部分のデータを1元配列として取り出してください
 ### 解答例2-2
```python:q2-2.py
>>> data[1,:,2]
array([213, 223, 233])
```
### 問題2-3 赤色部分のデータを1元配列として取り出してください
### 解答例2-2
```python:q2-2.py
>>> data[1,:,2]
array([213, 223, 233])
```
### 問題2-3 赤色部分のデータを1元配列として取り出してください
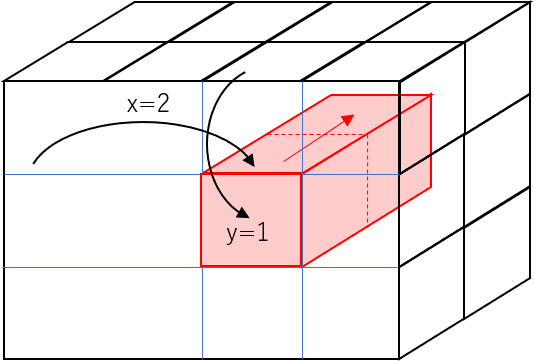 ### 解答例2-3
```python:q2-3.py
>>> data[:,1,2]
array([123, 223])
```
## 練習3 2次元配列の取り出し
### 問題3-1 赤色部分のデータを2元配列として取り出してください
### 解答例2-3
```python:q2-3.py
>>> data[:,1,2]
array([123, 223])
```
## 練習3 2次元配列の取り出し
### 問題3-1 赤色部分のデータを2元配列として取り出してください
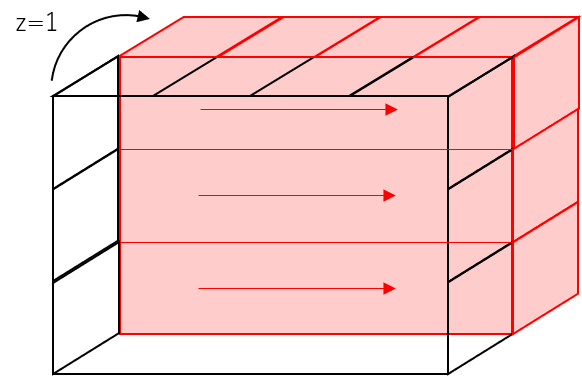 ### 解答例3-1
```python:q3-1.py
>>> data[1,:,:]
array([[211, 212, 213, 214],
[221, 222, 223, 224],
[231, 232, 233, 234]])
# 省略形
>>> data[1]
array([[211, 212, 213, 214],
[221, 222, 223, 224],
[231, 232, 233, 234]])
```
### 問題3-2 赤色部分のデータを2元配列として取り出してください
### 解答例3-1
```python:q3-1.py
>>> data[1,:,:]
array([[211, 212, 213, 214],
[221, 222, 223, 224],
[231, 232, 233, 234]])
# 省略形
>>> data[1]
array([[211, 212, 213, 214],
[221, 222, 223, 224],
[231, 232, 233, 234]])
```
### 問題3-2 赤色部分のデータを2元配列として取り出してください
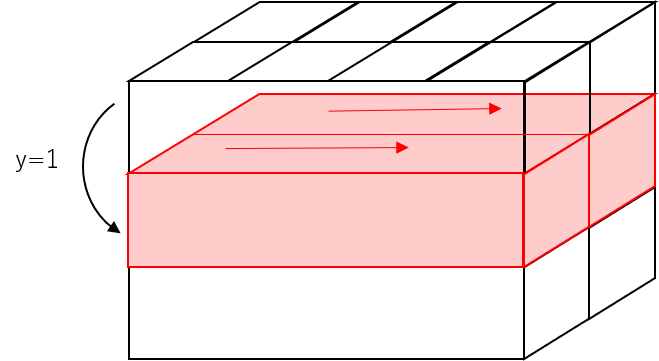 ### 解答例3-2
```python:q3-2.py
>>> data[:,1,:]
array([[121, 122, 123, 124],
[221, 222, 223, 224]])
# 省略形
>>> data[:,1]
array([[121, 122, 123, 124],
[221, 222, 223, 224]])
```
### 問題3-3 赤色部分のデータを2元配列として取り出してください
### 解答例3-2
```python:q3-2.py
>>> data[:,1,:]
array([[121, 122, 123, 124],
[221, 222, 223, 224]])
# 省略形
>>> data[:,1]
array([[121, 122, 123, 124],
[221, 222, 223, 224]])
```
### 問題3-3 赤色部分のデータを2元配列として取り出してください
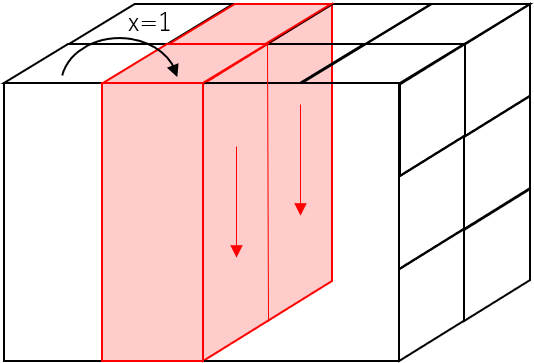 ### 解答例3-3
```python:q3-3.py
>>> data[:,:,1]
array([[112, 122, 132],
[212, 222, 232]])
```
### 解答例3-3
```python:q3-3.py
>>> data[:,:,1]
array([[112, 122, 132],
[212, 222, 232]])
```
練習4 スライス
問題4-1 図のZ方向に取り出した1次元配列の最初の要素をスライスします
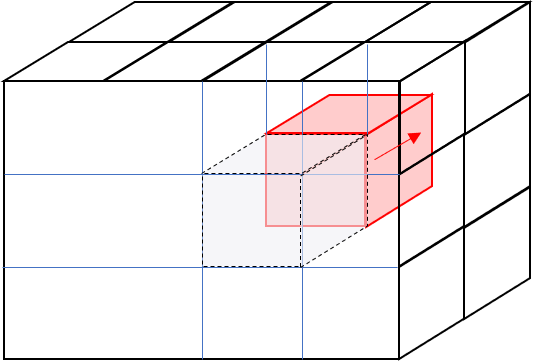 ### 解答例4-1
```python:q4-1.py
>>> data[1:,1,2]
array([223])
```
上の通り結果はスカラではなく配列です.
### 問題4-2 図ように取り出した2次元配列のyの最初の要素をスライスします
### 解答例4-1
```python:q4-1.py
>>> data[1:,1,2]
array([223])
```
上の通り結果はスカラではなく配列です.
### 問題4-2 図ように取り出した2次元配列のyの最初の要素をスライスします
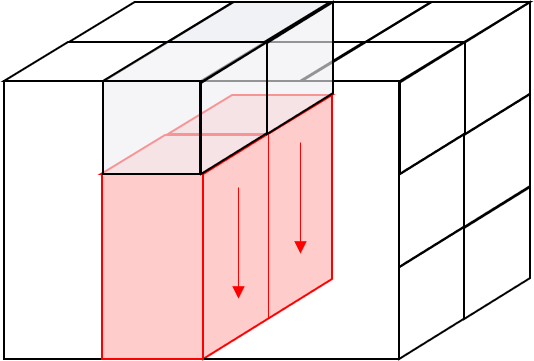 ### 解答例4-2
```python:q4-2.py
>>> data[:,1:,1]
array([[122, 132],
[222, 232]])
```
### 問題4-3 図ようにもとの配列をスライスします
### 解答例4-2
```python:q4-2.py
>>> data[:,1:,1]
array([[122, 132],
[222, 232]])
```
### 問題4-3 図ようにもとの配列をスライスします
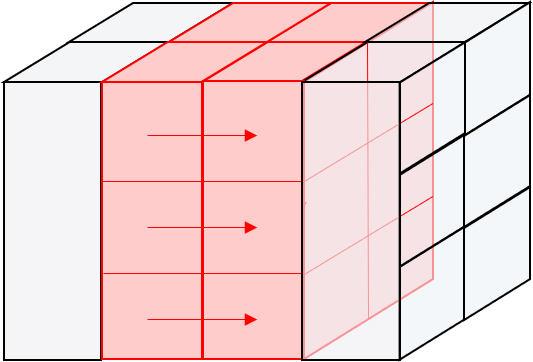 ### 解答例4-3
```python:q4-3.py
>>> data[:,:,1:3]
array([[[112, 113],
[122, 123],
[132, 133]],
### 解答例4-3
```python:q4-3.py
>>> data[:,:,1:3]
array([[[112, 113],
[122, 123],
[132, 133]],
[[212, 213],
[222, 223],
[232, 233]]])
## 練習5 分散図
### 問題5-1 図の赤い部分を2つの1次元配列とみなして,その関係を分散図として表示してください.
<img src="https://qiita-image-store.s3.ap-northeast-1.amazonaws.com/0/135512/b0f08152-4414-ed68-f6dd-300f22e27724.png" width=50%>
### 解答例5-1
```python:q5-1.py
>>> import matplotlib.pyplot as plt
>>> (data[0,1,:],data[1,1,:])
(array([121, 122, 123, 124]), array([221, 222, 223, 224]))
>>> plt.scatter(data[0,1,:],data[1,1,:])
<matplotlib.collections.PathCollection object at 0x0000019ACC48C208>
>>> plt.show()

問題5-2 図の赤い部分を2つの1次元配列とみなして,その関係を分散図として表示してください
 ### 解答例5-2
```python:q5-2.py
>>> (data[0,:,1],data[1,:,1])
(array([112, 122, 132]), array([212, 222, 232]))
>>> plt.scatter(data[0,:,1],data[1,:,1])
>>> plt.show()
```
### 解答例5-2
```python:q5-2.py
>>> (data[0,:,1],data[1,:,1])
(array([112, 122, 132]), array([212, 222, 232]))
>>> plt.scatter(data[0,:,1],data[1,:,1])
>>> plt.show()
```
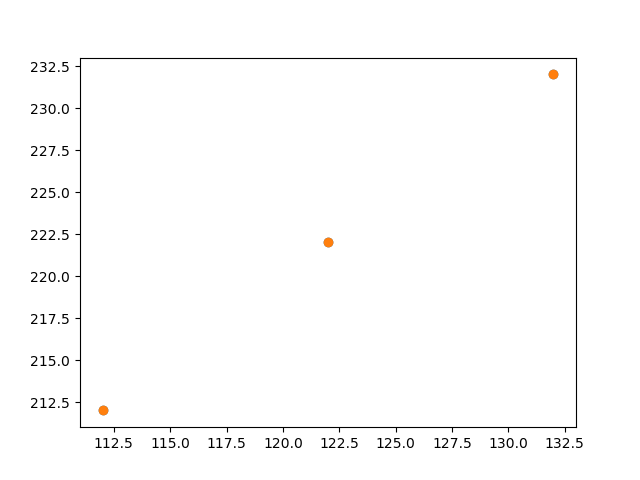
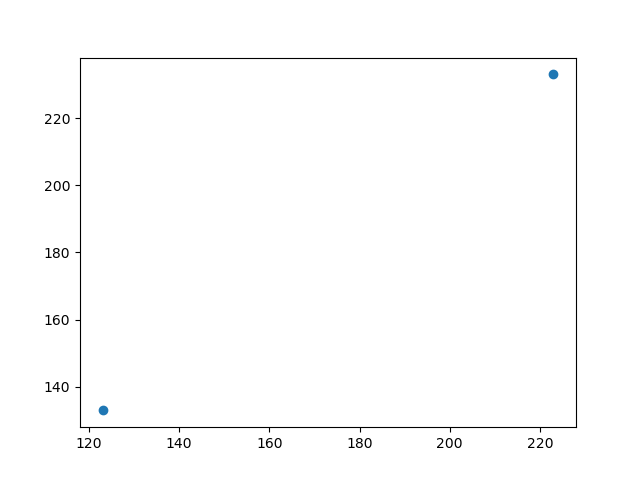
問題5-3 図の赤い部分を2つの1次元配列とみなして,その関係を分散図として表示してください
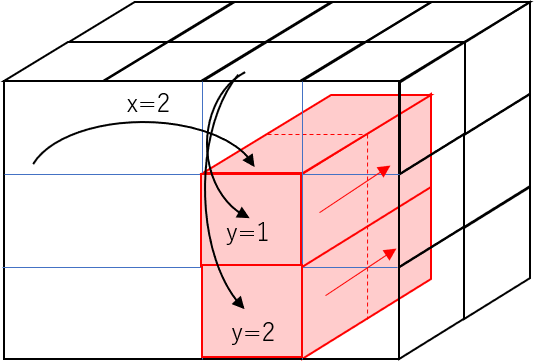
解答例5-3
q5-3.py
>>> (data[:,1,2],data[:,2,2])
(array([123, 223]), array([133, 233]))
>>> plt.scatter(data[:,1,2],data[:,2,2])
<matplotlib.collections.PathCollection object at 0x0000019AC70D1808>
>>> plt.show()