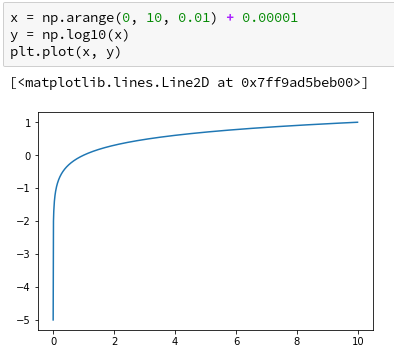
対数関数
高校数学で習ったような気がする、対数関数。
忘れてしまった人も多いのではないでしょうか。
「こんなもの覚えて何の役に立つんだ」と思って高校の授業を受けていた人もいたかもしれませんが、コンピュータの世界では、たまに出てきます。
- 統計や機械学習の式の中に出てくる
- 情報量の議論で出てくる
- アルゴリズムの話で、計算量のオーダーで
O(log N)などと出てくる
などです。
対数関数って一体何でしょう。どういう性質があるんでしょう。これらを見ていきましょう。
コードはPythonとJavaScriptで書いていますが、大抵の言語では同じようなものが用意されています。
納得するまで、手元で動かしてみることをおすすめします。
雑に言っちゃうと、桁数を求める関数です。
まずは、一番分かりやすい、常用対数と呼ばれるものを見ていきます。
常用対数はPythonではmath.log10 (numpyだとnumpy.log10)、JavaScriptではMath.log10です。
import math
[math.log10(x) for x in (1, 10, 100, 1000, 10000)]
# => [0.0, 1.0, 2.0, 3.0, 4.0]
[1, 10, 100, 1000, 10000].map(Math.log10)
// => [ 0, 1, 2, 3, 4 ]
逆に、0.1, 0.01, 0.001だとどうなるでしょう?
[0.1, 0.01, 0.001, 0.0001].map(Math.log10)
// => [ -1, -2, -3, -4 ]
マイナスになりました。
じゃあ、log10(0)やlog10(-1)は?
math.log10(0)
# => ValueError: math domain error
math.log10(-1)
# => ValueError: math domain error
おっ??
Math.log10(0)
// => -Infinity
Math.log10(-1)
// => NaN
おやおや??!
log10は、(0を含まない)正の数でのみ定義されているようです。0に近づくにつれ小さくなります。また、先程みたように、log10(1)が0で、それより小さくなるとマイナスになります。
さっきは1, 10, 100, 1000などのキリのいい数ばかり試しましたが。もうちょっと試してみましょう。
[math.log10(x) for x in range(1, 11)] # log10([1, 2, ..., 9, 10])
# => [0.0, 0.3010299956639812, 0.47712125471966244, 0.6020599913279624, 0.6989700043360189, 0.7781512503836436, 0.8450980400142568, 0.9030899869919435, 0.9542425094393249, 1.0]
[math.log10(x*10) for x in range(1, 11)] # log10([10, 20, ..., 90, 100])
# => [1.0, 1.3010299956639813, 1.4771212547196624, 1.6020599913279625, 1.6989700043360187, 1.7781512503836436, 1.845098040014257, 1.9030899869919435, 1.9542425094393248, 2.0]
実は、y = log10(x)とは、$10^y = x$になる$y$を探す計算なのです。
y = math.log10(1); print(y) # => 0.0
print(10**y) #=> 1.0
y = math.log10(10); print(y) # => 1.0
print(10**y) #=> 10.0
y = math.log10(0.1); print(y) # => -1.0
print(10**y) #=> 0.1
y = math.log10(2); print(y) # => 0.3010299956639812
print(10**y) #=> 2.0
浮動小数点なので、完全には一致しない可能性がありますが、概ねこうなります。
log10? 知りたいのはlogなんだけど?
log10の説明で、y = log10(x)とは$10^y = x$を探す関数だ、と書きました。
logとlog10の違いは、上式の10の部分を何の数字にするかの違いです。(この数字を「対数の底」と呼びます)
実は、この部分が何の数字になるのかは、分野によって違ったりします。
- 工学の分野には、10になる、つまりlog10と同じになる流儀が存在するようです
- 情報の分野では、2になる流儀が存在します
- 計算量のオーダーでは、対数の底を2で考えることが多いです
- 二分法で計算にかかる時間を求めるときに相性がよさそうですね
- 情報量(エントロピー)の定義でも、対数の底を2にすることが多いです
- 理学、数学では「ネイピア数」と呼ばれるものにすることが多いです
- ネイピア数を対数の底とする対数を「自然対数」と呼びます
- また、自然対数を$\log$で書かずに$\ln x$のように表記する流儀もあります
- ネイピア数は、Pythonでは
math.e、JavaScriptではMath.Eで定義されていて、2.718281828459045...のようになっています - また、指数関数(exp)は、ネイピア数をeとして $\exp(x) = e^x$という関係を持っています
Python, JavaScriptでは、math.log あるいは Math.log は、自然対数が使われています。
(ただし、Pythonでは、第2引数に対数の底を指定することも可能です)
この数字は、対数関数を微分しているうちに出てくるんですが、「この意味不明な数字にしておくと、数学的に都合がいいらしい」という雑な理解で構いません。
(ちゃんと理解したい方には、こちらのブログ記事がお勧めです)
常用対数と自然対数の関係
実は定数倍です。
[0.1, 0.2, 1, 2, 10, 20, 100, 200].map(Math.log10)
// => [ -1, -0.6989700043360187, 0, 0.3010299956639812, 1, 1.3010299956639813, 2, 2.3010299956639813 ]
[0.1, 0.2, 1, 2, 10, 20, 100, 200].map(Math.log)
// => [ -2.3025850929940455, -1.6094379124341003, 0, 0.6931471805599453, 2.302585092994046, 2.995732273553991, 4.605170185988092, 5.298317366548036 ]
// 試しに、割り算してみる。
[0.1, 0.2, 1, 2, 10, 20, 100, 200].map((x)=>Math.log10(x)/Math.log(x))
// => [ 0.43429448190325187, 0.4342944819032518, NaN, 0.43429448190325187, 0.43429448190325176, 0.43429448190325187, 0.43429448190325176, 0.43429448190325187 ]
// 0/0が発生したので、NaNがあるけど、どれもだいたい0.4342944...倍
Math.log10(Math.E) // => 0.4342944819032518 おお!!
常用対数と自然対数に限らず、次のような数式で、底の変換ができます。(ただし、ゼロ除算には気をつけて下さい)
$$\log_a x = \frac{\log_b x}{\log_b a}$$
ここで、$\log$の横に小さく書いてある数字が対数の底です。
logを使って、常用対数を求めてみましょう。
[10, 100, 1000, 10000].map((x)=>Math.log(x)/Math.log(10))
// => [ 1, 2, 2.9999999999999996, 4 ]
若干の誤差はありますが、出ました。
また、単に定数倍の関係になっているため、対数の底が何であっても
\log x
\begin{cases}
> 0 & (x > 1)\\
= 0 & (x = 1) \\
< 0 & (0 < x < 1) \\
\end{cases}
になっており、$x \le 0$では対数を計算できないことも覚えておいてください。
対数を使うと何が嬉しいか?
いろんな場面で対数関数は出てくるのですが、一体なんでこんなの使うんでしょう?
グラフを描くとき
数字が非常に大きくなる場合、y軸を対数スケールにすると分かりやすくなることがあります。
ムーアの法則のように指数関数的に増えるものは、対数スケールにすると(すごく上がってる感は薄くなりますが)見やすくなります。
また、通常は為替には対数スケールは使いませんが、Wikipediaのジンバブエ・ドルの項目には、ハイパーインフレが起こった際の為替を対数スケールで表示したグラフが載っています。
x軸も対数スケールにした「両対数グラフ」というものも、たまに使われます。
例えば$y = x^k$のグラフを両対数グラフで表すとしましょう。$Y = \log y$, $X = \log x$と置くと、両対数グラフでは、$\log y = \log x^k \Rightarrow Y = kX$のような形になり、kが傾きとして出てきます。($\log x^k = k \log x$という公式を使っています)
掛け算、割り算を多用するとき
対数には、禿げ上がるほどクソ便利な公式があります。
$$\log xy = \log x + \log y$$$$\log \frac{x}{y} = \log x - \log y$$
掛け算が足し算に、割り算が引き算になるんです。
機械学習などで使う、対数尤度関数なんかは、尤度関数だと掛け算を多用するから、それを足し算に変換できるのは嬉しいですね。
1以下の数字を何度も掛け算していくと、どんどん0に近づいていって計算できなくなるので、対数を取っているという事情もありそうなので、そういう意味では前に挙げた例と同じなのですが。
機械学習の本とかを読んでいて、掛け算がなぜか足し算になっていることに戸惑った人もいるかもしれませんが、対数を使うとそうなります。
アルゴリズムの計算量では勝手に出てくることも
例えば、二分法での検索を考えましょう。ソートされた配列のどこに、目的の数字があるのかを探す場合、まず真ん中を見て、それよりも小さいか大きいかで、さらにその真ん中を見るのが2分法でした。
N要素の中から目的の数字を探す場合に、何回見たら答えが分かるでしょうか? 1回見るたびに、候補を半分に減らせるので、見る回数をxとすると
$2^x = N$
ということになります。
これは、対数を使って $x = \log_2 N$と表せます。
デシベルやマグニチュードも対数
音圧レベル(音の大きさ)の単位でデシベル(dB)というのを聞いたことありませんか?
これは、「人間に聞こえる最小の音圧の何倍の音圧か?」を常用対数で表して10倍したものです。
つまり、10 dB上がると、常用対数が1大きくなるので、10倍の音圧ということになります。
20 dBだと、2大きくなるので、10x10 = 100倍の音圧です。
また、デシベルは通信などでの増幅・減衰を表す場合にも使われます。
増幅や減衰などは「エネルギーが100増える」などではなく「エネルギーが10倍になる」とか、そういう起こり方をする場合が多いのですが、対数で表すと都合がいいです。
増幅器をつなげたとき、デシベルの足し算で議論できるのも楽です。
また、地震のエネルギーを表すマグニチュードは、$\sqrt{1000}\approx 31.6$を底とする対数で表されており、マグニチュードが2増えると地震のエネルギーは1000倍になります。
まとめ
- 対数は、雑に言うと、桁数を求める関数。対数の底によって定数が掛かっている
- 0やマイナスの値は対数を取れないので気をつける
- 対数の底が何であっても、$\log 1 = 0$, $\log x < 0\ (0 < x < 1)$, $\log x > 0\ (x > 1)$
- 掛け算が足し算になるなどの便利な公式がある
- 大きい数字や、ゼロに近い数字を扱いやすくするのによく使われる
- 対数は怖くない