量子回路シミュレータのノイズモデル

量子コンピュータの実機は、外部からのノイズの影響で計算途中にエラー(誤り)が生じます。
そのため、従来のコンピュータで動作させる、量子回路のシミュレータでの理想的な実行結果との差が生じます。

では、量子回路のシミュレータで、エラーのある実機の動作を真似ることはできるでしょうか。
Qiskitでは、ノイズモデルという形でそれをサポートしています。

エラーのモデルとノイズモデル

これらのライブラリでは、量子回路にエラーを入れるために2段階でのモデル化を行っています。

1. エラー自体のモデル化。どのような確率で量子ビットがどのように変化するかをモデル化する
2. ノイズモデル。量子回路のどこに、上でモデル化したエラーが現れるかをモデル化する

まずはQiskitのエラーのモデルを見ていきます。

Qiskitのエラーモデル

Qiskitのパートは大体ここを参考にしています。

Qiskitには、エラーは、量子状態に対するエラー(QuantumError)と、測定時に測定値を読み誤るエラー(ReadoutError)があります。

今回はReadoutErrorについては深く取り上げません。

量子状態に起こるエラーとして、最も一般的なものはKraus表現ですが、より直感的なエラーを見ていきます。

Pauli エラー

一定の確率で、bit flipやphase flipが起こるエラーを考えます。

以下のようにすると、確率0.1でXゲートが入り、0.9でIゲートが入る(つまりエラーが起こらない)エラーを作ることができます。

bit flip エラー

from qiskit.providers.aer.noise import *
err = pauli_error([('X', 0.1), ('I', 0.9)])
print(err)

QuantumError on 1 qubits. Noise circuits:
  P(0) = 0.1, Circuit = 
   ┌───┐
q: ┤ X ├
   └───┘
  P(1) = 0.9, Circuit = 
   ┌───┐
q: ┤ I ├
   └───┘

また、同様に、意図せずZゲートが入るphase flipエラーを書くこともできます。

phase flip エラー

from qiskit.providers.aer.noise import *
err = pauli_error([('Z', 0.1), ('I', 0.9)])
print(err)

QuantumError on 1 qubits. Noise circuits:
  P(0) = 0.1, Circuit = 
   ┌───┐
q: ┤ Z ├
   └───┘
  P(1) = 0.9, Circuit = 
   ┌───┐
q: ┤ I ├
   └───┘

depolarization エラー

これは、一定の確率で量子ビットに関する情報が完全にデタラメになってしまうエラーです。
ブロッホ球で描くと、通常はブロッホ球の半径は1ですが、それが小さくなってしまう、というイメージを持つと直感的です。

1量子ビットで考えられる嫌なエラーのひとつとして、よく用いられます。

depolarization エラー

err = depolarizing_error(0.1, 1)
print(err)

QuantumError on 1 qubits. Noise circuits:
  P(0) = 0.925, Circuit = 
   ┌───┐
q: ┤ I ├
   └───┘
  P(1) = 0.025, Circuit = 
   ┌───┐
q: ┤ X ├
   └───┘
  P(2) = 0.025, Circuit = 
   ┌───┐
q: ┤ Y ├
   └───┘
  P(3) = 0.025, Circuit = 
   ┌───┐
q: ┤ Z ├
   └───┘

amplitude damping エラー

ある確率で、重ね合わせが破壊されて、確率p0で$|0\rangle$に、p1で$|1\rangle$になるエラーです。

熱緩和エラー

実用上は、このエラーが一番重要です。
熱緩和エラーは、物理系で実装された量子ビットが、熱による影響を受けて起こる誤りをモデル化していて、2つのパラメータからなります。

T1: $|1\rangle$ が $|0\rangle$ にRESETされる時間を表す
T2: 位相が分からなくなる時間を表す

最近調べた際、実機ibmq_manillaでは、T1が平均162.83 μs, T2が平均61.64 μsでした。
CNOT操作は平均368 nsで行っています。

これらの値を当てはめると、

熱緩和エラー

print(thermal_relaxation_error(161.83e3, 61.64e3, 368))

QuantumError on 1 qubits. Noise circuits:
  P(0) = 0.9958881145044123, Circuit = 
   ┌───┐
q: ┤ I ├
   └───┘
  P(1) = 0.0018404778295728285, Circuit = 
   ┌───┐
q: ┤ Z ├
   └───┘
  P(2) = 0.0022714076660148574, Circuit = 
        
q: ─|0>─

Iの部分の確率が約0.996なので、エラーが0.004の確率で起きています。これは、実際のエラー率よりやや低いですが、桁としては近い値です。

エラーの作り方を見る

以下は、Qiskitのチュートリアルのコードの引用です。

4量子ビットの系を作るために、以下のようにエラーを定義しています。

Example 2の前半

# T1 and T2 values for qubits 0-3
T1s = np.random.normal(50e3, 10e3, 4) # Sampled from normal distribution mean 50 microsec
T2s = np.random.normal(70e3, 10e3, 4)  # Sampled from normal distribution mean 50 microsec

# Truncate random T2s <= T1s
T2s = np.array([min(T2s[j], 2 * T1s[j]) for j in range(4)])

# Instruction times (in nanoseconds)
time_u1 = 0   # virtual gate
time_u2 = 50  # (single X90 pulse)
time_u3 = 100 # (two X90 pulses)
time_cx = 300
time_reset = 1000  # 1 microsecond
time_measure = 1000 # 1 microsecond

# QuantumError objects
errors_reset = [thermal_relaxation_error(t1, t2, time_reset)
                for t1, t2 in zip(T1s, T2s)]
errors_measure = [thermal_relaxation_error(t1, t2, time_measure)
                  for t1, t2 in zip(T1s, T2s)]
errors_u1  = [thermal_relaxation_error(t1, t2, time_u1)
              for t1, t2 in zip(T1s, T2s)]
errors_u2  = [thermal_relaxation_error(t1, t2, time_u2)
              for t1, t2 in zip(T1s, T2s)]
errors_u3  = [thermal_relaxation_error(t1, t2, time_u3)
              for t1, t2 in zip(T1s, T2s)]
errors_cx = [[thermal_relaxation_error(t1a, t2a, time_cx).expand(
             thermal_relaxation_error(t1b, t2b, time_cx))
              for t1a, t2a in zip(T1s, T2s)]
               for t1b, t2b in zip(T1s, T2s)]

T1, T2を正規分布からランダムに設定しています。
物理的な制約からT1とT2の関係には制約があり、制約を満たさないものを書き換えています。
量子ゲートによって実行時間が異なるため、熱緩和エラーが異なってきます。そのため、ゲートごとの実行時間を定義しています。

これらのパラメータから、 thermal_relaxation_error を作っています。

このように、量子ビットごと、量子ゲートごとにエラーを定義しました。ここから、ノイズモデルに埋め込んでいきます。

ノイズモデル

ノイズモデルは、エラーを量子回路にどのように埋め込むかをモデル化します。Qiskitでは、以下のように行います。

再びQiskitのチュートリアルのコードを引用します。

Example 2の後半

noise_thermal = NoiseModel()
for j in range(4):
    noise_thermal.add_quantum_error(errors_reset[j], "reset", [j])
    noise_thermal.add_quantum_error(errors_measure[j], "measure", [j])
    noise_thermal.add_quantum_error(errors_u1[j], "u1", [j])
    noise_thermal.add_quantum_error(errors_u2[j], "u2", [j])
    noise_thermal.add_quantum_error(errors_u3[j], "u3", [j])
    for k in range(4):
        noise_thermal.add_quantum_error(errors_cx[j][k], "cx", [j, k])

NoiseModel() でノイズモデルを作成して、 add_quantum_error(エラーモデル, "ゲート名", [量子ビット番号]) でエラーをモデルに加えています。

このように、Qiskitでは、量子ビットごと・量子ゲートごとにエラーをノイズモデルに埋め込むことができ、比較的細かく設定ができます。

ノイズモデルを使ったシミュレーション

ノイズモデルを使った量子回路の実行は、以下のようにバックエンドを作る際にnoise_modelを指定することで行えます。

ノイズモデルを使ったシミュレーション

from qiskit import QuantumCircuit, execute
from qiskit.providers.aer import AerSimulator
from qiskit.tools.visualization import plot_histogram

circ = QuantumCircuit(2, 2)
# Run the noisy simulation
backend = AerSimulator(noise_model=noise_thermal)
# Run and get counts
counts_thermal = execute(circ, backend).result().get_counts()

# Plot noisy output
plot_histogram(counts_thermal)

ノイズの効果を実感してみる

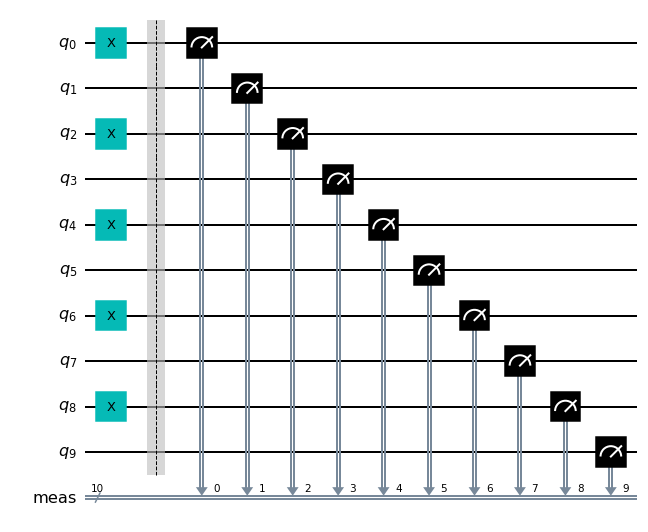
こんな回路を考えます。

ただXがあるだけの回路

n = 0
qc = QuantumCircuit(10)
qc.x([2 * i for i in range(5)])
qc.measure_all()
qc.draw("mpl")

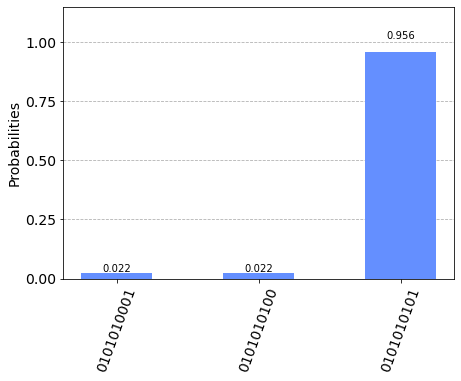
この測定値は(Qiskitでは右から左に向かって測定結果を並べるので) 0101010101がノイズがない場合の理想です。
ノイズつきシミュレータで動かしても、ほぼ理想通りの結果が得られています。

shots = 1000
backend = AerSimulator(noise_model=noise_thermal)
counts_thermal = execute(qc, backend, shots=shots, optimization_level=0).result().get_counts()

plot_histogram(counts_thermal)

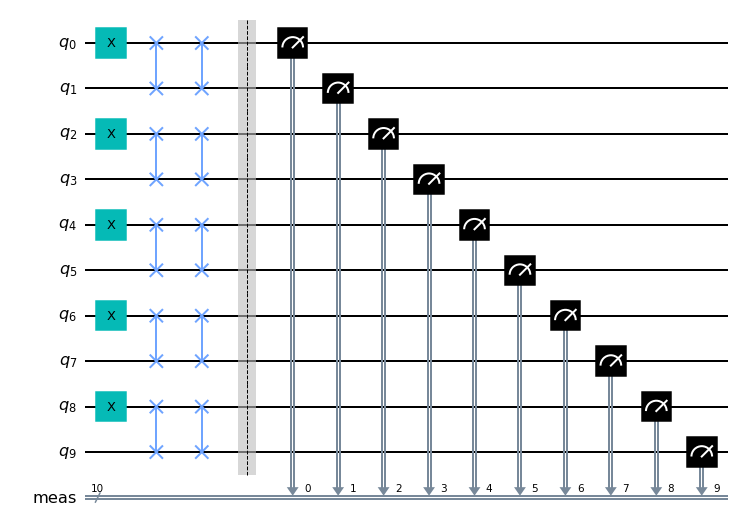
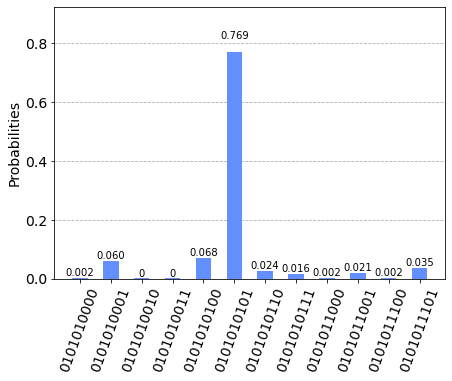
ここに、無駄なSWAPを付け加えます。実行時にoptimization_level=0で、トランスパイラが無駄なSWAPを削除するのを防止していることに気をつけてください。この操作をしても理想的には0101010101が出るはずです。

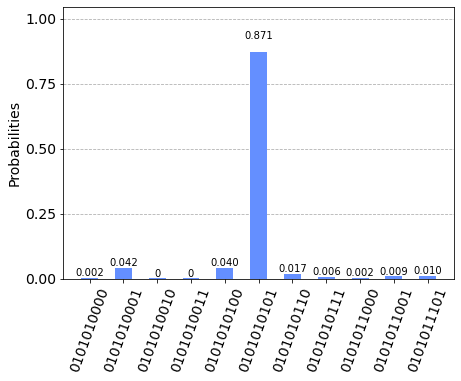
すると、

さらに無駄なSWAPを増やすと

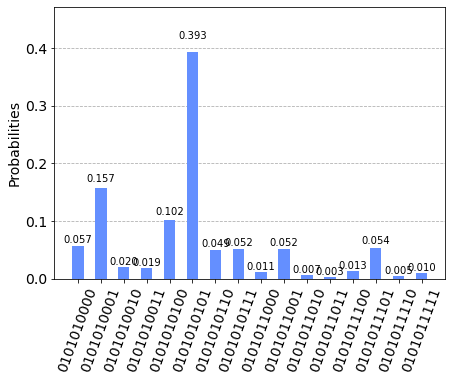
SWAP2回を10セット繰り返すと

正しい結果は4割弱でしか得られなくなりました。

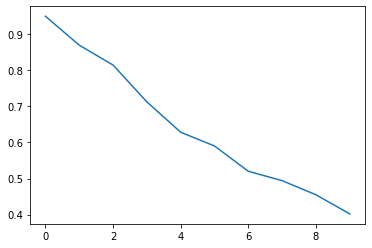
回数が増えるごとの正しい結果を得る確率は、以下のようになりました。

このように、回路が長くなれば、エラーが大きくなっていく様子が見えました。

まとめ

• Qiskitでのノイズモデルを使ったシミュレーションを見た
• 個々のエラーを表すエラーモデルと、それを回路に埋め込んだノイズモデル
• ノイズありのシミュレーションでは、回路が長くなればエラーが大きくなっていく様子がわかる