そういえば、ベン図書いてなんとなく分かった気になってたけど、対偶って本当に等しいんだっけ? と気になったので、Coqで証明してみました。

対偶とは

「AならばB」の対偶は、「BでないならばAでない」です。
再び対偶を取れば元に戻る¹ので、
「BでないならばAでない」の対偶は「AならばB」です。

対偶を考えるメリットですが。対偶を取っても、真偽は一致します。
つまり

「AならばB」が真ならば、「BでないならばAでない」も真
「AならばB」が偽ならば、「BでないならばAでない」も偽

が常に成り立ちます。また、同様に

「BでないならばAでない」が真ならば、「AならばB」も真
「BでないならばAでない」が偽ならば、「AならばB」も偽

も成り立ちます¹。

ベン図による理解

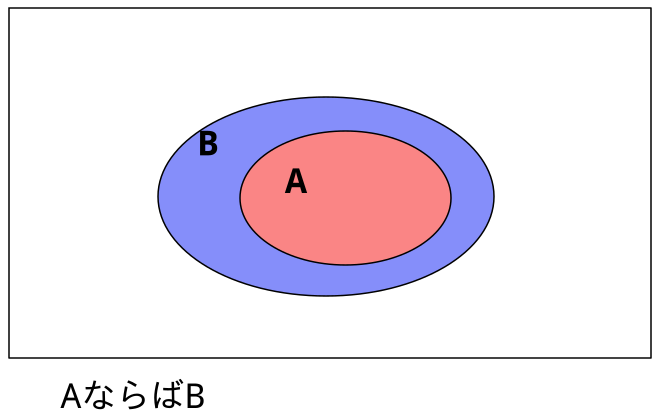
命題AとBをマルで表すことにしましょう。すると、「AならばB」は、Bのマルの中にAのマルがおさまっている形になります。

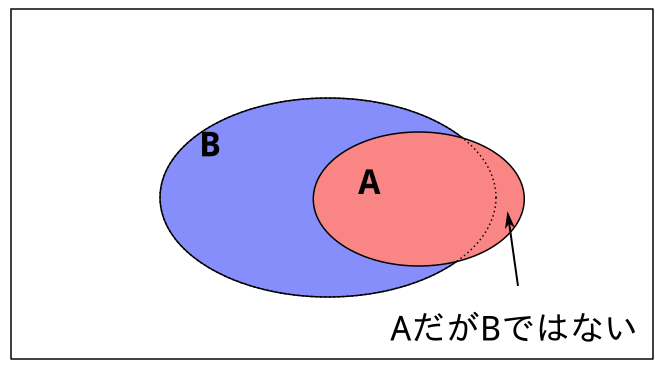
おさまらずにはみ出している部分がある場合、Aであるにも関わらずBでない部分が出てきてしまいます。

さて、Aの否定、Bの否定を考えます。この場合、マルの外側に色を塗ります。
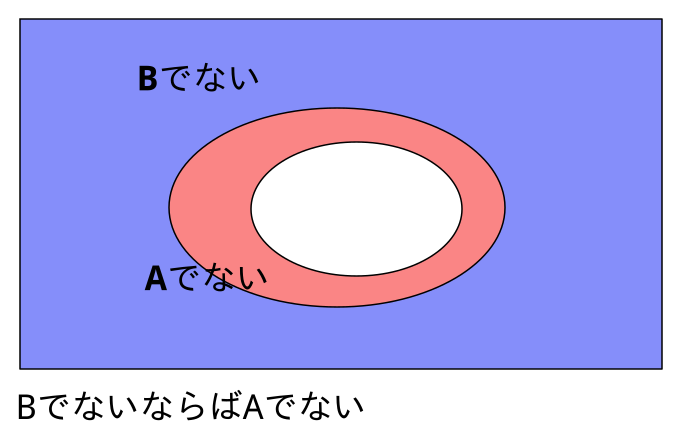
「AならばB」の図の、マルの内側を塗っていたのを、外側を塗るように変えると、以下のようになります。

すこし分かりにくいですが、「Aでない」の中に「Bでない」がおさまっています。
つまり、「BでないならばAでない」です。

Coqで証明してみる

Coq自体の説明については、ソフトウェアの基礎などをご覧ください。

対偶が等しいことを示したいので、次の2つの定理を証明します。

Section contraposition.

Theorem contraposition1 : forall A B: Prop,
  (A -> B) -> (~B -> ~A).
Proof.
  Abort.

Theorem contraposition2 : forall A B: Prop,
  (~B -> ~A) -> (A -> B).
Proof.
  Abort.

End contraposition.

最初のが、「AならばB」ならば「BでないならばAでない」で、2つ目が「BでないならばAでない」ならば「AならばB」です。

1つ目のTheoremの証明

最初のひとつは簡単に証明ができました。

Theorem contraposition1 : forall A B: Prop,
  (A -> B) -> (~B -> ~A).
Proof.
  intros A B ab notb a.
  apply notb.
  apply ab.
  apply a.
Qed.

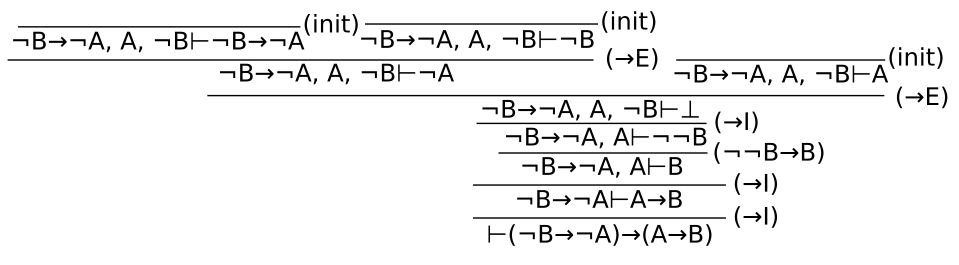
証明図で書くと、次のようになります²。

2つ目のTheoremの証明(?)

2つ目もやってみましょう。

Theorem contraposition2 : forall A B: Prop,
  (~B -> ~A) -> (A -> B).
Proof.
  intros A B nbna a.

ここからBを証明するって、どうするん?

大切なことはWikipediaに全部書いてあった

上述の対偶の性質は古典論理におけるそれであり、非古典論理においては成立しない場合がある。例えば直観主義論理においては、必ずしも「AならばB」とその対偶「BでないならAでない」の真偽は一致しない。
直観主義論理の特徴として、排中律の不成立（あるいは二重否定の除去の制限）があげられるが、対偶の性質はこの制限の影響を受け成立しない。なお「AならばB」から「BでないならAでない」は、直観主義論理においても導出可能である。
Wikipedia 対偶(論理学)#直観主義論理における扱い

Coqの論理は直観主義論理なので、"「BでないならばAでない」ならば「AならばB」"は成り立ちません！　ゆえに証明できません！
……では、つまらないので、仮定を入れてみましょう。

古典論理ってなに?

大切なことはWikipediaに全部書いてあるので、再び読んでみると。
直観主義論理は「排中律の不成立（あるいは二重否定の除去の制限）」という特徴があるので、成立しないようです。
古典論理も調べてみると、排中律が成立することや二重否定の除去が成り立つのが特徴のようです。

二重否定の除去を使って証明する

二重否定の除去を導入して証明してみましょう。
二重否定の除去とは「not not AならばA」です。
「Aならばnot not A」は直観主義論理でも言えるのですが、「not not AならばA」は直観主義論理では一般には言えません。

Section contraposition.

Hypothesis classical : forall A: Prop,
  ~~A -> A.

Theorem contraposition2_classical : forall A B: Prop,
  (~B -> ~A) -> (A -> B).
Proof.
  intros A B nbna a.
  apply classical.
  intros nb.
  apply nbna.
  apply nb.
  apply a.
Qed.

End contraposition.

できた!

証明図も書いてみました。

二重否定の除去はどう書くのか分からなかったので怪しい書き方をしています。
(直観主義論理に二重否定の除去を仮定したもの、と考えるなら、⊢の左側に書いて証明した方がよかったかもしれません)

排中律を仮定してやってみる

排中律でも構わないようですので、やってみます。
排中律とは「すべての命題は真または偽である」ということで、証明の手法としては、ある命題について「真の場合」「偽の場合」と場合分けをして考えることができるようになります。
(逆に、排中律が成立していなければ、そういった場合分けはできません)

Hypothesis classical' : forall A: Prop,
  A\/~A.

Theorem contraposition2_classical' : forall A B: Prop,
  (~B -> ~A) -> (A -> B).
Proof.
  intros A B nbna a.
  destruct (classical' B) as [b|nb].
  - apply b.
  - elimtype False.
    apply nbna.
    apply nb.
    apply a.
Qed.

destructのところで、Bが真の場合と偽の場合に場合分けしています。
Bが真のときは、当然「AならばB」は成り立ちます。
一方、Bが偽のときは、「BでないならばAでない」が成り立つならばAではなく、それゆえ「AならばB」は(前提が偽なので)成り立ちます。

まとめ

Coqを使って、直観主義論理で「A→Bのとき、¬B→¬A」を示しました。
また、二重否定の除去や排中律の成立を仮定して、「¬B→¬Aのとき、A→B」も示しました。
めでたしめでたし。

少なくとも古典論理では。 ↩
証明図の書き方はこちらを参考にしました。 ↩

Coqで対偶は等しいことを証明してみた