以前、Pythonで自由群$F_2$を作ってみました。
今回はその続きで、二面体群$D_4$を作ってみます。
二面体群とは?
平らな正n角形を思い浮かべてください。今回は、$D_4$を作るので、正方形を思い浮かべます。
この正方形について、
- 操作r: 正方形を時計回りに360/n度回転する
- 操作t: 正方形を裏表ひっくり返す
- 操作e: なにもしない
の3つの操作を考えます。
また、これらの積(複数の操作を順に行う)や、逆元(rの逆元は、反時計回りに回転する, tの逆元はt)を考えることもできます。また、「なにもしない」操作eは単位元に相当します。
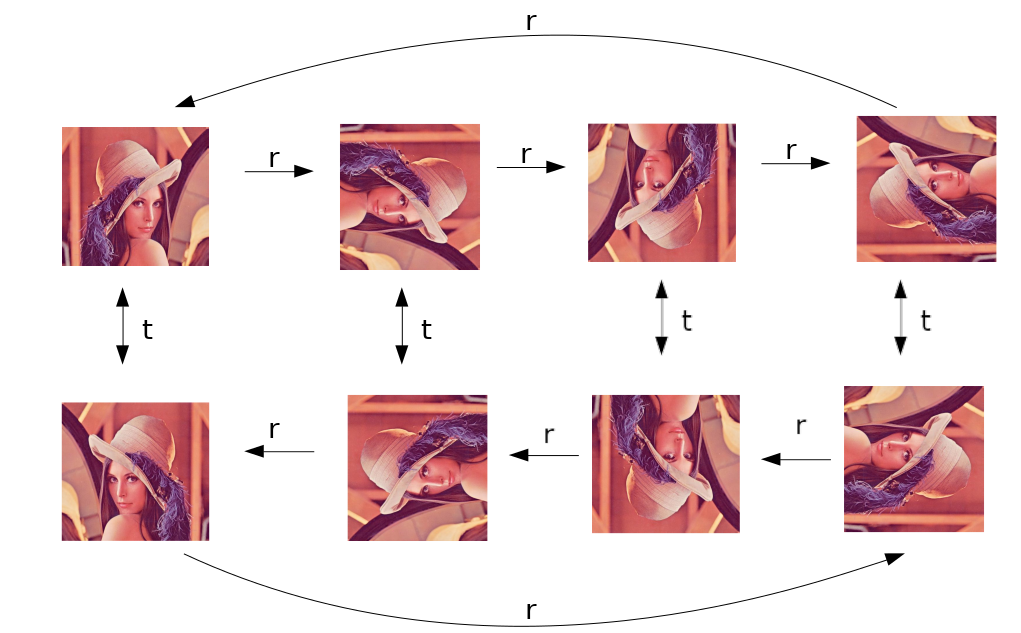
$r^{-1}$を書くのをサボっていますが、図にすると、次のようになります。
2つの元r, tから生成される、という点では、自由群$F_2$と似ているのですが、自由群になかった特徴として、
$r^4 = e$, $t^2 = e$ や、さらには $trt = r^{-1}$ という性質があります。(3つ目の性質に気づかれていましたでしょうか? 裏返して時計回りに回転して、再び裏返すと、反時計回りに回転したことになっている、ということを言っています)
実は、どんな群でも、自由群にこういった関係式を付け加えることで作ることができる、というのは知っておいて損はないかもしれません。
実装していきましょう
簡単な形にしたい
自由群のときと同じように、文字列で保持するのですが、関係式を考慮しながら、できるだけ簡単な形にしておきたいです。
まず、$t^{-1}$は$t$に、$r^{-1}$は$r^3$に置き換えることができます。($r\cdot r^{3} = e$なので$r^{-1} = r^{3}$です)
さらに$t^2 = e$, $r^4 = e$も考慮すると、rとtの数を数えて、4で割った余り、2で割った余りを取ればいいことが分かります。
もっと簡単にならないでしょうか。
$trt = r^{-1}$ がありましたが、右から$t$をかけると、$t^2 = e$を考慮すると$tr = r^{-1}t$となります。
$trrt = trttrt = r^{-1}r^{-1}$となります。これを繰り返すと$tr^nt = tr^{-n}t$が分かります。
上と同様に、$tr^n = r^{-n}t$となります。
これを繰り返すことで、r...rtr...rtr...rtとなっているのを、r...rtの形に、tを右にずらせることが分かります。
結果、どんな元でも、正規表現で書くと 'r{,3}t?' の形 (0〜3個のrと、0個または1個のt)で書けることが分かります。
積を考える
tの有無で場合分けして考えます。
- $(r^n t)\cdot(r^m t)$のとき⇒$r^{n-m}$になります
- $(r^n t)\cdot(r^m)$のとき⇒$r^{n-m}t$になります
- $(r^n)\cdot(r^m t)$のとき⇒$r^{n+m}t$になります
- $(r^n)\cdot(r^m)$のとき⇒$r^{n+m}$になります
つまり、左側にtがあればrの数がn-mに、なければn+mになります。
また、最後にtがつくかどうかは、tの個数が奇数か偶数かで決まります。
逆元を考える
自由群のときと同じように、文字列を逆転して、また、すべてを逆元にするといいのですが、簡単な形式に直すことを考えると、次のように場合分けできます。
- $(r^n)^{-1} = r^{-n}$
- $t^{-1} = t$
- $(r^n t)^{-1} = t r^{-n} = r^n t$
なんと、tがついていたら、自分自身が逆元になるんですね。面白い。
コード
前回作ったFreeGroupBaseを親クラスにしていきます。
from collections import namedtuple
FreeGroupBase = namedtuple('FreeGroupBase', 's')
さらに、先ほど考察したことをコードに書き起こします。
import re
class DihedralGroup(FreeGroupBase):
'''rとtの2つの元からなる群で、r^n = e, t^2 = e, trt = r^-1を満たす。
ここでは、n=4 (D_4)とした。
'''
check = re.compile('r{,3}t?')
def __init__(self, s: str):
if not self.check.fullmatch(s):
raise ValueError('Unexpected format')
def __mul__(self, other: 'DihedralGroup') -> 'DihedralGroup':
return DihedralGroup(self._reduction(self.s, other.s))
def __invert__(self) -> 'DihedralGroup':
# ~(r^n) = r^{-n}
# ~t = t
# ~(r^n t) = t r^{-n} = r^n t
if not self.s or self.s[-1] == 't':
return self
return DihedralGroup('r' * (4 - len(self.s)))
@staticmethod
def _reduction(lhs: str, rhs: str) -> str:
# r^4 = e, t^2 = t, trt = r^-1 の関係式がある。
# trt = r^-1は、tr = r^-1 tと読み替えられるので、これを使って、tを右に寄せていく
# また、r^-k (k>0)のような形が残った場合、r^{n-k}に置き換える
# 結果的に、正規表現で書くと r{,4}t? の形にまとめられる。
# lhs, rhsは、既にこの処理が済んでいると考える
def count(s):
'"r{,3}t?" で表された文字列のrの数とtの数を返す'
if not s:
return 0, 0
if s[-1] == 't':
return len(s) - 1, 1
return len(s), 0
r1, t1 = count(lhs)
r2, t2 = count(rhs)
if t1:
r2 = -r2
return 'r' * ((r1 + r2) % 4) + 't' * ((t1 + t2) % 2)
def __repr__(self) -> str:
if not self.s:
return 'e'
return ' * '.join(self.s)
やってみる
print(t * r * t)
print(t * r * t * r)
print(t * r * r * r * t)
print(e * e * t * r * e * r * e * e * e * r * t)
print(r * r * t * r)
print(~(r*r*r) * (r*r*r))
print(~(r*r*r*t) * (r*r*r*t))
r * r * r
e
r
r
r * t
e
e
なんかできてそう。
まとめ
今回、二面体群をPythonで作ってみました。
二面体群は、簡単ながらも、化学計算などで分子の対称性を考えるときなどにも使われる有用な群です。