何がしたいの?
計算グラフをぶった切って、オリジナルな微分を定義しよう
今回やること
計算グラフのぶった切りが発生する状況はいろいろ考えられると思いますが、複雑な関数だと合ってるのか合ってないのか分からないので、今回は単純な関数を文字列にしてevalで評価する関数を用意します。いくら計算が単純でも、さすがにPyTorchはそんなの面倒見きれないので、計算グラフがぶった切られることになります。
また、そうすると自分で微分を定義しないといけないですが、今回は前進差分法
$$\frac{\partial f(x, w)}{\partial w} = \frac{f(x, w + \Delta w) - f(x, w)}{\Delta w}$$
を使うことにします。
欠点
PyTorchを使う理由のひとつである自動微分を使わないことで、コードが複雑化する。今回の場合、やる必要がないし、速度も遅くなる。
利点
今回やることには、利点はないです。
けれど、どうしても計算グラフをぶった切りたい場合に、とりあえずできる、という何物にも代えがたい利点があります。
一方、もしどうしても無理なら、モデルを考え直す、本当にPyTorchを使ってそれをやらなければいけないのか考え直す、という風になると思うのですが、とりあえずできてしまうため、それを考え直す機会が失われてしまいます。
それでもどうしてもやりたい場合にはどうぞ。
(ぼくは、それでもどうしてもやらなきゃいけなかった)
それでは、やっていきましょう
次のような関数を考えるよ
めちゃくちゃ簡単なものを考えてみます。
# どちらも同じですが、f_strは、さすがにこんなの、PyTorchでは、微分を面倒見きれません。
# 入力は、x, wともPyTorchのTensor型を想定しています。
def f(x, w):
return 2 * x * w[0] + x**2 * w[1]
def f_str(x, w):
return torch.tensor([eval(f'2 * {x_} * {w[0]} + {x_}**2 * {w[1]}') for x_ in x])
fは見たまんまです。f_strは、fと同じなんですが、一旦文字列にして、evalでPython式に解釈しなおして計算しています。
入力xはバッチで入ってくる可能性を考えて、f_strの方では、一旦中身をバラしてtensorを作り直しています。
torchの賢い自動微分
x = torch.tensor([1.])
w = torch.tensor([1., 1.]).requires_grad_()
f(x, w) # => tensor([3.], grad_fn=<AddBackward0>)
y.backward()
w.grad # => tensor([2., 1.])
PyTorchは賢いので、fでやったことが全部すべてまるっとお見通しで、y.backward()したらw.gradが自動でできます。PyTorchを始めとする機械学習フレームワークを使う理由のひとつがこれだと思います。
自動微分できない愚かな関数
先ほど、f_strを大変愚かしい作り方をしたのを覚えているかと思います。この場合、次のような憂き目に遭います。
x = torch.tensor([1.])
w = torch.tensor([1., 1.]).requires_grad_()
f_str(x, w) # => tensor([3.]) grad_fnがない!!!!
y.backward() # RuntimeError: element 0 of tensors does not require grad and does not have a grad_fn
w.grad # => None
なんかgrad_fnがないなー、と思ったら、backwardしたらエラーでるし、gradはセットされてないし、散々です。
まずは、普通に作った方を学習させてみよう
データを作ろう
actual_w = 1.2, -3.4
xs = np.random.rand(200).astype(np.float32)
ys = np.array([f(x, actual_w) for x in xs], dtype=np.float32)
train_d = torch.utils.data.TensorDataset(torch.from_numpy(xs), torch.from_numpy(ys))
train_loader = torch.utils.data.DataLoader(train_d, batch_size=10)
v_xs = np.random.rand(10).astype(np.float32)
v_ys = np.array([f(x, actual_w) for x in v_xs], dtype=np.float32)
valid_d = torch.utils.data.TensorDataset(torch.from_numpy(v_xs), torch.from_numpy(v_ys))
valid_loader = torch.utils.data.DataLoader(valid_d, batch_size=1)
真のwとして、適当に値をセットします。で、適当に乱数振って、xとf(x, 真のw)の組を作ります。
さらにこれにガウシアン乱数とか載せたらいいんでしょうけど、面倒なので、今回そういうことしません。
こんなん、PyTorch使うのはオーバーキルです。scipy.minimize.optimizeとか、そんなんで十分だと思います。
普通に学習させてみる
class Model(torch.nn.Module):
def __init__(self):
super().__init__()
self.weight = torch.nn.parameter.Parameter(torch.tensor([0., 0.]))
def forward(self, x):
return f(x, self.weight)
model = Model()
optimizer = torch.optim.Adam(model.parameters(), lr=0.1)
criterion = torch.nn.MSELoss()
loss_hist = []
model.train()
for epoch in range(20):
for i, (xs, l) in enumerate(train_loader):
out = model(xs)
loss = criterion(out, l)
loss_hist.append(loss)
optimizer.zero_grad()
loss.backward()
optimizer.step()
print(epoch, loss, model.weight)
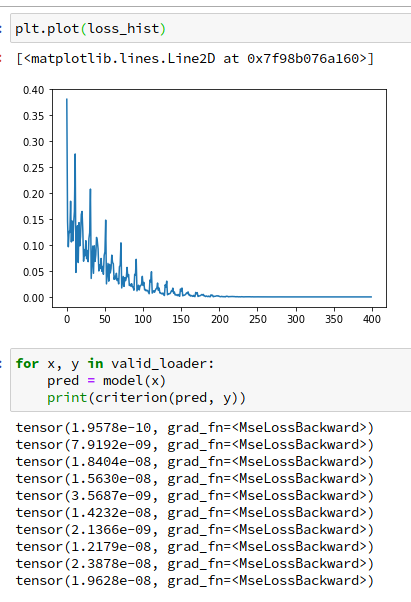
model.weightは最終的に1.1996, -3.3987になりました。1.2, -3.4を真の値として設定したので、ほぼほぼあっています。学習中のlossと、validation用に用意したデータでのloss (全部ほぼ0になっていると成功)は
のようになりました。だいぶよさそうですね。
fをf_strに変えてみる
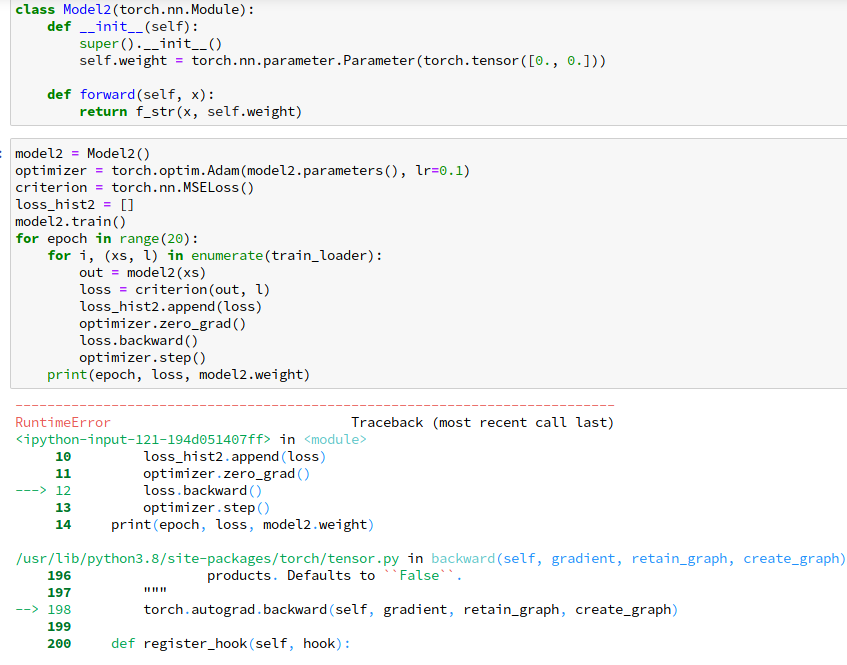
さて、fをクソ関数のf_strに変えてみましょう。
だいぶ分かりにくいエラーですが。言わんとしていることは簡単で。f_strで計算グラフがぶった切られて、自動微分ができなくなったから、backwardでコケているわけです。ということで、自分で微分を定義する必要があります。
キミだけの微分を作ろう
こういう場合の方法は、公式ドキュメントだとここに載っています。
けれど、実際やってみて、かゆいところに手が届かなかったので、そこらへんを紹介します。
まずはコード、そして解説
class GeneralFunctionWithForwardDifference(torch.autograd.Function):
@staticmethod
def forward(ctx, f, xs, weight):
ys = f(xs, weight)
ctx.save_for_backward(xs, ys, weight)
ctx.f = f # 実はctxにも何かを保存できて、backwardで使える
return ys
@staticmethod
def backward(ctx, grad_output):
xs, ys, weight = ctx.saved_tensors
f = ctx.f
dw = 0.001
diff = []
weight = weight.detach() # weightに余計な計算履歴を残さないために、detachする。
for i in range(len(weight)):
weight[i] += dw
diff.append(torch.sum(grad_output * (f(xs, weight) - ys)))
weight[i] -= dw
diff = torch.tensor(diff) / dw
return None, None, diff
torch.autograd.Functionを継承したクラスを作ること、また、@staticmethodでforward, backwardを定義すること、各々の第一引数はctxとすること(別名でもいいけど、こういうのには従っておくとよい)などは、ドキュメントにあるとおりです。
テンソル以外のデータの保存
ctx.save_for_backwardでテンソルを保存できるとドキュメントにありますが、この方法ではtorch.Tensor以外は保存できません。
けれど、今回はforwardの引数にf_strを渡して、それをbackwardのために保存したいのです。
実はこれ、ctx.なんちゃら = ...の形で保存することができ、これはbackwardで使うことが出来るようです。Pytorch内部でも使われているので、おそらく、使ってもいいんじゃないかと思います。
backwardは何を返せばいいの?
backwardで返す値は、forwardの引数に対応しています。forwardの引数からctxを除いたものの微分結果を返していきます。
微分が必要ないもの(テンソルじゃないものや、required_grad=Trueじゃないテンソル)に対応している箇所はNoneを返せばいいです。今回、wのみが微分が必要です。
入力がテンソル${\bf w} = [w_0, w_1, ..., w_{n-1}]$の場合、返す値は
[\sum_i\mathrm{grad\_output}_i\frac{\partial f(x_i, {\bf w})}{\partial w_0}, \sum_i \mathrm{grad\_output}_i\frac{\partial f(x_i, {\bf w})}{\partial w_1}, ... \sum_i\mathrm{grad\_output}_i\frac{\partial f(x_i, {\bf w})}{\partial w_{n-1}}]
となります。ただし、$\sum_i$は、入力xがミニバッチ$[x_0, x_1, ...]$で来た場合に、各々の結果を足し合わせることを言っています。grad_outputの次元はミニバッチの大きさに対応しているので、このように結果に掛け合わせます。
ようやくf_strを使った方も学習が出来る
class Model2(torch.nn.Module):
def __init__(self):
super().__init__()
self.weight = torch.nn.parameter.Parameter(torch.tensor([0., 0.]))
def forward(self, x):
# 書くのが若干めんどくさい。
return GeneralFunctionWithForwardDifference.apply(f_str, x, self.weight)
model2 = Model2()
optimizer = torch.optim.Adam(model2.parameters(), lr=0.1)
criterion = torch.nn.MSELoss()
loss_hist2 = []
model2.train()
for epoch in range(20):
for i, (xs, l) in enumerate(train_loader):
out = model2(xs)
loss = criterion(out, l)
loss_hist2.append(loss)
optimizer.zero_grad()
loss.backward()
optimizer.step()
print(epoch, loss, model2.weight)
作ったFunctionは、.applyの形で呼び出すことに注意しましょう。
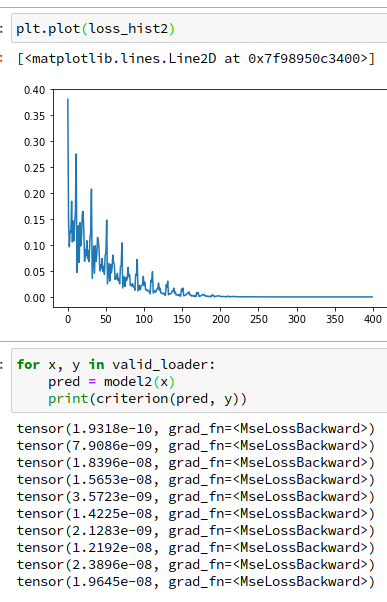
どっか間違えたんちゃうかって思うほど、さっきのと似たグラフが出てきました。
最終的なパラメータも 1.1996, -3.3987と、やはり真の値の1.2, -3.4とほぼ一致する値になりました。
まぁ、乱数とか使わず、同じデータで同じパラメータ初期値でやってるから、そうなるんでしょうね。知らんけど。
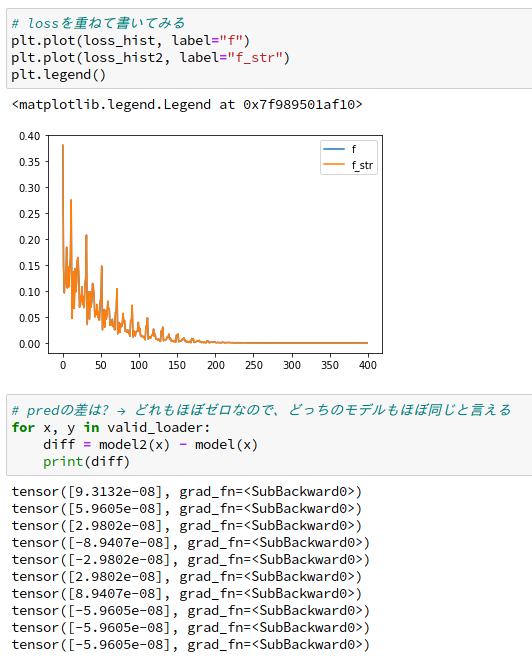
ついでに、lossを重ねて描いてみたり、validationの予測値の差分をとってみたりしました。
ほぼほぼ一致してます。
いい加減な微分を使ったので、多少差が出るかと思ったら、大した違いがなさそうです。よかったです。
まとめ
計算グラフをぶった切るような変な関数を、自分で微分を定義して無理矢理PyTorchで使う方法を見ていきました。もうやりたくありません。
今回のノートブックをこちらに置いときます