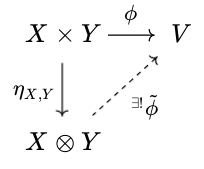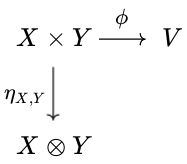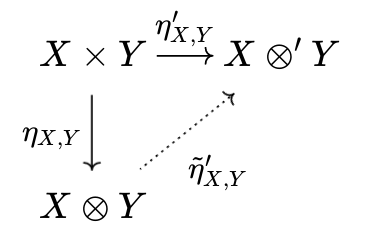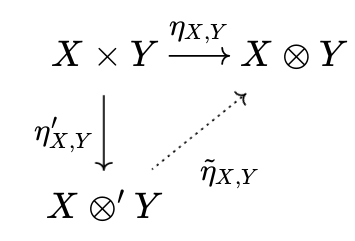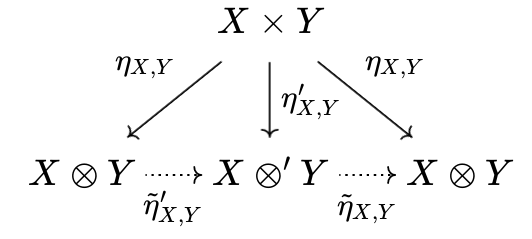はじめに
量子力学では、量子状態をベクトルとして扱うことが多い。そして複数の量子状態を合成した系を考える際にテンソル積を導入する。その際、テンソル積の定義にクロネッカー積を採用している。
一方で、数学では、テンソル積をクロネッカー積としてではなく、双線形写像とその普遍性で定義しているものも見かける。本記事は、クロネッカー積によるテンソル積の定義を理解している読者に、普遍性によるテンソル積の定義のイメージを掴んでもらうことを目標としている。
量子力学におけるテンソル積
量子力学においてテンソル積が必要になるのは、複数の系を合成して、ひとつの系と考えたいためだ、といえる。本記事では、2つの系を1つの系に合成することにフォーカスを当てて議論する。合成する系の数が有限であれば、2つずつ合成を繰り返すことで1つの系とできるので、このように考えても問題がない。また、本記事で扱うベクトル空間も、有限次元のものに限ることとする。
2つの系が相互作用を持たない独立した系で、また、系の間での情報通信もないとすれば、片方の系のみに対する操作は、もう片方の系には影響せず、それぞれの系を個別に扱うのと変わらないはずである。つまり、テンソル積は、そのような独立した系においてはテンソル積を取らずに個別に系を考えたときと同じ振る舞いをすることが期待される。
局所的な操作の他に、系の間での情報通信を許容することで、2つの系は相関を持つことができる。さらに系の間に相互作用がある場合には「量子もつれ状態」と呼ばれる状態を取りえる。これは個別に系を考えた場合には決して得られないことが知られている。しかし、合成系もまたベクトル空間であり、量子もつれ状態であっても、状態は、各基底ごとに係数を掛けて重ね合わせた、ひとつのベクトルとして整合的に振る舞う。
こういった要求を満たすベクトル空間として、2つの系のテンソル積があり、また、テンソル積を構成するための演算としてクロネッカー積がある。
普遍的な双線形写像としてのテンソル積
テンソル積の普遍性による定義は、クロネッカー積による構成的な定義とは一見、かなり違ったものに見える。しかしこれらは、本質的な意味では同じものであることを後に見る。
記法
以下では、次の記法を用いる。
- $x \in X$は、要素$x$が$X$に属していることを表す。
- $X \times Y$とは、$X$と$Y$との集合論的な直積である。すなわち、$x \in X$と$y \in Y$を組にしたもの$(x, y)$の集合であり、形式的な書き方をすれば$X \times Y = \{(x, y) \mid x \in X, y \in Y\}$である。
- $X \rightarrow Y$のような記法は、$X$から$Y$への写像(=関数)を表す。
- $\phi: X \rightarrow Y$のように書けば、写像$\phi$が$X$から$Y$への写像であることを表す。
- $(x, y) \in X \times Y$に写像$\phi: X \times Y \rightarrow Z$を適用する操作は、字義通りに書けば$\phi((x, y))$となるが、$\phi(x, y)$と略記する。(すなわち、$\phi$を2引数関数のように見ることにする)
- $\phi \circ \phi'$ は、写像の合成であり、 $(\phi \circ \phi')(x) = \phi(\phi'(x))$を意味する。
- ある集合$A$とその部分集合$X \subseteq A$があったとき、$\mathrm{span}(X)$は$X$の元を基底としてとったベクトル空間を表す。
双線形写像
テンソル積の定義を示す前に、双線形写像の定義を確認する。
定義: 2つのベクトル空間$X, Y$の組をベクトル空間$V$に移す写像$\phi: X \times Y \rightarrow V$が双線形写像であるとは、$\phi$が以下の性質を満たすことをいう。
- 任意の$x_1, x_2 \in X, y \in Y$について、$\phi(x_1 + x_2, y) = \phi(x_1, y) + \phi(x_2, y)$を満たす
- 任意の$x \in X, y_1, y_2 \in Y$について、$\phi(x, y_1 + y_2) = \phi(x, y_1) + \phi(x, y_2)$を満たす
とくに、
$$\phi(\sum_i x_i, \sum_j y_j) = \sum_i \sum_j \phi(x_i, y_j) $$
が成り立つことを後に使う。
ベクトル空間の組は、ベクトル空間ではないことに注意する。
例えば、$\{|0\rangle, |1\rangle\}$を基底に持つベクトル空間を$\mathbf{2}$と書くことにする。$(|0\rangle, |0\rangle), (|1\rangle, |1\rangle) \in \mathbf{2}\times\mathbf{2}$であるが、$(|0\rangle, |0\rangle) + (|1\rangle, |1\rangle)$はうまく定義されているだろうか? ($\mathbf{2}\times\mathbf{2}$同士の足し算は、再び$\mathbf{2}\times\mathbf{2}$の元、つまり、$\mathbf{2}$の組になっていなければならない。もし、うまい定義を思いついたなら、$(|0\rangle, |0\rangle) + (|1\rangle, |1\rangle) - (|0\rangle, |1\rangle) - (|1\rangle, |0\rangle)$が何になるかを考えてほしい)
双線形写像は、ベクトル空間の組をベクトル空間に変換する。
テンソル積は、普遍的な双線形写像として定義される。
普遍的な双線形写像としてのテンソル積の定義
定義: 2つのベクトル空間$X, Y$のテンソル積とは、あるベクトル空間$X \otimes Y$と双線形写像$\eta_{X, Y}: X \times Y \rightarrow X \otimes Y$の組であって、以下の「普遍性」を満たすものである。
普遍性: 任意のベクトル空間$V$と双線形写像$\phi: X \times Y \rightarrow V$の組に対し、$\phi = \tilde \phi \circ \eta_{X, Y}$となるような$\tilde \phi$がただ一つ存在する。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
まず気をつけるべきは、この定義は$X \otimes Y$の具体的な構成を与えていないことだ。つまり、所与の性質を満たす何らかのベクトル空間に$X \otimes Y$という名前を付けたとしか言っていない。さらに言うならば、このような性質を満たすベクトル空間がそもそも存在するのか(また、存在するとして一つに定まるのか)についても、まだ示していない。
であるので、具体的な$X \otimes Y$について考えることは脇に置いて、上に書いた性質がどのようなものかを考える。
ベクトル空間$X$と$Y$は固定して考える。$X, Y$から、どこでもいいのでベクトル空間$V$に行くような双線形写像をなんでもいいので取ってくる。例えば、ベクトル空間$V$と双線形写像$\phi: X \times Y \rightarrow V$を取ってきたとする。
状況を整理しよう。いま、$X \times Y$を出発点とする、2つの双線形写像を考えている。ひとつは$X \otimes Y$へと行く$\eta_{X, Y}$で、もうひとつが$V$へと行く$\phi$である。また、$V$および$\phi$の選び方は任意であった。
このとき、$(V, \phi)$が何であったとしても、それに対応した線形写像$\tilde{\phi}: A \otimes B \rightarrow V$が存在していて、$\phi = \tilde{\phi} \circ \eta_{X, Y}$を満たすこと、また、これを満たす$\tilde{\phi}$の作り方はただ一つしかない。そのような性質を$\eta_{X, Y}$が満たすことを言っている。
別の言い方をすれば、$\phi$は、$X \otimes Y$を経由した形に書き換えることができ、また、その書き換えは1通りに定まる。$X \otimes Y$は、ベクトル空間の組$X \times Y$に「できる限り近づけた」ような、最も一般的なベクトル空間であると考えてもよい。
クロネッカー積はテンソル積である
以上の議論を見ても、テンソル積の定義が非常に曖昧で、そのようなものが存在するのかすら明らかでないように思われる。そこで、具体的な構成方法であるクロネッカー積が、テンソル積の性質を満たしていることを示す。
クロネッカー積
ベクトル空間$X, Y$を固定し、また、$X$の基底$\{|x_1\rangle, ..., |x_n\rangle\}$, $Y$の基底$\{|y_1\rangle, ..., |y_m\rangle\}$を選ぶ。$K = \mathrm{span}(\{|x_1\rangle, ..., |x_n\rangle\}\times\{|y_1\rangle, ..., |y_m\rangle\})$と置くと、$k: X \times Y \rightarrow K$を、各基底の組を$k(|x_i\rangle, |y_j\rangle) = |x_i y_j\rangle$に移す双線形写像として定義する。
$X$の元、$Y$の元はベクトル空間なので、それぞれ、基底を使って$\sum_i x_i |x_i\rangle, \sum_j y_j |y_j\rangle \in Y$と書き表すことができる。上では、$k$の行き先を、明示的には各基底ごとにしか与えていないが、元を基底を使って書き直せることと、双線形性より、任意の$\sum_i x_i |x_i\rangle \in X, \sum_j y_j |y_j\rangle \in Y$について、
$$k(\sum_i x_i |x_i\rangle, \sum_j y_j |y_j\rangle) = \sum_i \sum_j x_i y_j |x_i y_j\rangle$$
と、一意的に定まる。このように定めたベクトル空間$K$と、双線形写像$k$の組を、クロネッカー積と呼ぶ。
クロネッカー積はテンソル積の性質を満たしている
双線形写像$\phi: X \times Y \rightarrow V$を任意に取る。双線形性より、任意の$\sum_i x_i |x_i\rangle \in X, \sum_j y_j |y_j\rangle \in Y$について、
$$
\phi(\sum_i x_i |x_i\rangle, \sum_j y_j |y_j\rangle)
= \sum_i \sum_j x_i y_j \phi(|x_i\rangle, |y_j\rangle)$$
がいえる。
ここで、$\tilde{\phi}: K \rightarrow V$について、
$$\tilde{\phi}(\sum_{i, j} k_{i, j} |x_i y_j\rangle) = \sum_{i} \sum_j k_{i, j} \phi(|x_i\rangle, |y_j\rangle)$$
と定義すると、任意の$\sum_i x_i |x_i\rangle \in X, \sum_j y_j |y_j\rangle \in Y$について$(\tilde{\phi} \circ k)(\sum_i x_i |x_i\rangle, \sum_j y_j |y_j\rangle) = \phi(\sum_i x_i |x_i\rangle, \sum_j y_j |y_j\rangle)$であることが計算できるので、$\tilde{\phi} \circ k = \phi$であることが分かる。
また、$\phi' \circ k = \phi$となるような$\phi': K \rightarrow V$が与えられたとき、任意の$K$の基底が$k$によって作れることから、$\phi' = \tilde{\phi}$が示せる。
よって、クロネッカー積はテンソル積の性質を満たしている。
クロネッカー積とテンソル積は実質的に等しい
ここまでで、クロネッカー積がテンソル積の性質を満たしているもののうちの一つであることを見た。では、クロネッカー積以外でテンソル積の性質を持つベクトル空間、双線形写像の組み合わせは存在しないだろうか。これについては、実は存在しているかもしれない。しかし、テンソル積の性質を持つものは多数あったとしてもそれらは全て同型であることが知られている。ここで、同型であるとは、ベクトル空間$V, W$について、線形写像$\phi: V \rightarrow W, \psi: W \rightarrow V$で$\psi \circ \phi = I, \phi \circ \psi = I$を満たすようなものが存在することをいう。ただし$I$は恒等写像(なにも変化しない写像。単位行列をかけることに相当する)である。
クロネッカー積はテンソル積(のうちのひとつ)であるので、テンソル積の性質より、テンソル積同士が同型を除いて一意であることが言えれば、クロネッカー積とテンソル積は(せいぜい、同型写像が作れる範囲でしか違いがないという意味で)同じものとみなせる。
$$X \otimes Y \cong K$$
テンソル積は同型を除いて一意である
2つのテンソル積を$(\eta _ {X, Y}, X \otimes Y), (\eta' _ {X, Y}, X \otimes' Y)$
ととる。(クロネッカー積があるテンソル積と同型であることを考えるときは、$\eta'_{X, Y} = k, X \otimes' Y = K$と置けばいい)
このとき、
および
を組み合わせると、
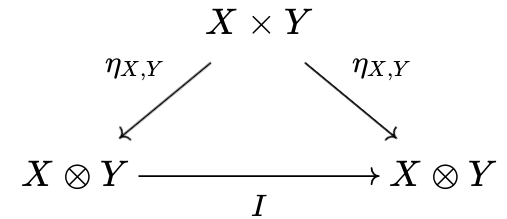
であるが、
もまた成り立ち、$\tilde{\eta} _ {X, Y} \circ \tilde{\eta}' _ {X, Y} = I$である。同様に$\tilde{\eta}' _ {X, Y} \circ \tilde{\eta} _ {X, Y} = I$も示される。よって、
$$ X \otimes Y \cong X \otimes' Y$$
がいえる。
参考文献
- 堀田昌寛. 入門 現代の量子力学 量子情報・量子測定を中心として. 講談社, 2021.
- S.マックレーン. 圏論の基礎. 三好博之, 高木理 訳. 丸善出版, 2012.
- T.レンスター. ベーシック圏論. 斎藤恭司監修, 土岡俊介訳. 丸善出版, 2017.
- Wikipedia
- nLab tensor product