量子ゲートで、非常に基本的なゲートにCNOTゲートがあります。
これは、Controlビットが1のときのみ、Targetビットを反転させる、というものです。
また、少し応用的なゲートにToffoliゲートがあります。
これは、Controlが2つあるCNOTゲートで、Controlビットが両方共1のときのみ、Targetビットを反転させる、というものです。
では、Controlが3つ, 4つ, ... の場合も、こうしたゲートを作ることができるのでしょうか。
このような、Multi-controlled NOTゲートを作っていきます。
基本方針
まず、Multi-controlled Zゲートを作ります。
続いて、Multi-controlled Zゲートの前後をHゲートで挟みます。
そうすると、Multi-controlled NOTゲートができます。
Targetビットに注目しましょう。
もしも、controlビットに0が含まれていた場合、Multi-controlled Zゲートは、Targetビットに何も起こりません。
すると、Targetビットには、Hゲートが2回適用されることになるので、何も起こりません。
もしも、controlビットがすべて1だった場合、Multi-controlled Zゲートによって、TargetビットにZゲートがかけられます。
すると、Targetビットには、 H, Z, H の操作がなされます。
これは、Xゲートを操作するのと等価であることが知られています。
こういったゲート操作がどのような行列になるのかを知るには、Blueqatを使うのが便利です。
from blueqat import Circuit
print(Circuit().h[0].z[0].h[0].run(backend='sympy_unitary'))
# => Matrix([[0, 1], [1, 0]])
print(Circuit().x[0].run(backend='sympy_unitary'))
# => Matrix([[0, 1], [1, 0]]) 上と同じ
Controlled RZゲートを作る
Controlled RZゲートは、Z軸を任意の角度だけ回転させるRZゲートの、controlled版です。
Multi-controlled Zゲートを作るために必要になるので、先に作っておきます。
これはとても簡単で、角度θを回転させるControlled RZは、次のように作ります。ただし、cはcontrolビット、tはtargetビットです。
CXはCNOTと同じ意味です。
rz(θ/2) t
cx c, t
rz(-θ/2) t
cx c, t
cが0のときは、CXゲートは何もしないので、
ターゲットビットは、θ/2回転した後、-θ/2回転し、元に戻ります。
cが1のときは、CXゲートはtをX軸周りに180度回します。
ターゲットビットは、θ/2回転した後、X軸まわりに180度回ります。それから-θ/2回転すると、回転は打ち消し合わず、追加で回ります。それから、X軸まわりに180度回したのを元に戻す操作をします。
イメージしにくいので、次のように、時計を考えます。面倒なので、短針だけ描いています。
(ブロッホ球が分かる人向けの説明: ブロッホ球のXY平面を輪切りにしたと思ってください)
4時間分、回転するには、次のようにします。
Multi-controlled RZゲートを作る
Multi-controlled RZゲートを作って回転角をπにすれば、Mutli-controlled Zゲートになるので、Multi-controlled RZゲートを作っていきます。
Controlled RZゲートを上で作りましたが、その際に行った、「回して、CNOTして、逆方向に回す」という方針はMulti-controlled RZゲートにも使えます。
全てのcontrolビットが1のときだけ、所定の回数を回るようにして、そうでないときは元に戻るようにする、というのが基本方針となります。
Controlが2個だと
回転したい角度をθとして、φ=θ/2とおきます。φが2回で、ちょうどθだけ回ることになります。
controlビットをc0, c1とおきます。また、targetビットをtとおきます。
まず、さっき作ったcrzを使いましょう。
crz(φ) c0, t // (1)
これだと、c1が0のときにも回転してしまうので、次のように対処します。
cx c0, c1
crz(-φ) c1, t // (2)
さらに、
cx c0, c1
crz(φ) c1, t // (3)
とします。
動きがわかりにくいので、表にします。
ただし、c0 c1: tの順で、tには、回転した角度の累計を書いています。
| 最初 | (1) | (2) | (3) |
|---|---|---|---|
| 0 0 | 0 0: 0 | 0 0: 0 | 0 0: 0 |
| 0 1 | 0 1: 0 | 0 1: -φ | 0 1: 0 |
| 1 0 | 1 0: φ | 1 1: 0 | 1 0: 0 |
| 1 1 | 1 1: φ | 1 0: φ | 1 1: 2φ |
ちょうど、c0, c1が1のときのみ2φ=θ、回転していることが分かります。
Grayコード
じゃあ、controlが3ビット、4ビット、...だったら、どうするのか。
自分でがんばって探さないといけないのか、規則性にしたがって自動で構成する方法があるのか。
気になると思います。
Grayコードを使うと、自動的にMulti-controlled RZゲートを作ることができます。
これは、nビットの数を、順に1ビットずつ変化させる符号化形式で、例えば、3ビットのGrayコードは次のようになります。
000
001
011
010
110
111
101
100
機械的に構成する
Grayコードを使って、次のような手順で構成します。
また、ターゲットとなるビットをTビットと表します。
- controlの数と同じビット数のGrayコードを考える。最初は0とする
- Grayコードを1つ進める。このとき「変化したビットが何番目か」、「立っているビットのうち最上位のものは何番目か」「立っているビットが偶数個か奇数個か(Grayコードの性質上、偶数、奇数、偶数、奇数、と繰り返す)」を覚えておく
- 変化したビットの番号をcontrol、最上位ビットの番号をtargetとして、CNOTゲートをかける。ただし、最上位ビットが変化した場合は、ひとつ下位のビットをcontrolとする。また、初回、0から1に進める場合は、CNOTはかけない
- 最上位ビットをcontrol、Tビットをtargetにして、crzゲートをかける。ただし、回転角は、立っているビットが奇数個のときはφ、偶数個のときは-φとする
- 2.に戻る。Grayコードを進めた結果、controlの数を超えたビットが立ったら6.に進む
- これにより、controlが全部1のときのみTビットが$2^{n-1}\phi$(ただしnはcontrolの数)回転し、それ以外はTビットが回転しない操作ができた。なので、$\phi = \theta/2^{n-1}$とおくと、θを回転させるmulti controlled RZゲートができた
すみません、なんでこれでできるのかは、まだ理解していません。
(知っている方がいたら、コメントいただけると有り難いです)
とりあえず、4ビットで回路を書いてみます。
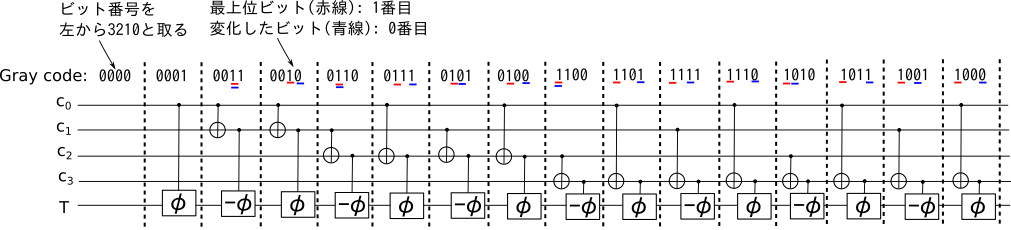
た、多分あってるはず……!
Multi-controlled RZゲートからMulti-controlled NOTゲートに
Multi-controlled RZゲートをMulti-controlled Zゲートとして使いたいので、回転角を180度、つまりθ = π (rad)とします。
Multi-controlled Zゲートのtargetビットの前後にHゲートを挿入すると、Multi-controlled NOTゲートができました。
参考文献&謝辞
この記事の大部分は、Qiskit Aquaのソースコードリーティングで得られた知見を元に書いています。
また、ソースコードリーディングは、MDR株式会社でのインターンの一環として、インターン生の助けをたくさん借りて行いました。
IBMの開発者とMDRのインターン生に深く感謝を申し上げます。