はじめに

友人たちと、古典のカーネル法について勉強をしていた。それが一通り終わったので、量子カーネル法について自分が知っていることをまとめて、友人に紹介することにした。
そのまとめを公開するが、そういった経緯から、この記事は線形代数やカーネル法を既に学んだことのある読者をターゲットとしている。

線形代数

複素数体での線形代数を、実数体での線形代数と比較する形で軽く触れる。
また、量子コンピュータでよく用いられるブラケット記法についても触れる。

複素数体での線形代数

実数体と比べて特徴的な違いを、以下に述べる。

エルミート共役または転置複素共役とは、行列やベクトルの転置を取り、また、値の複素共役を取る操作である。行列$A$のエルミート共役を$A^\dagger$で表す
- 実数行列における転置を複素数行列に拡張したものと考えることができる
- $(A^\dagger)_ {ij} = (A _ {ji})^*$ である。ただし、$ {}^ * $は複素共役を表している
エルミート行列とは、$A = A^\dagger$を満たすような行列$A$のことである
- 実数行列における対称行列を複素数行列に拡張したものと考えることができる
ユニタリ行列とは、$UU^\dagger = U^\dagger U = I$を満たすような行列$U$のことである。ここで、$I$は単位行列である
- すなわち、ユニタリ行列$U$については、$U^{-1} = U^\dagger$である
- 実数行列における直交行列を複素数行列に拡張したものと考えることができる
- 直交行列と同様、$U_1, U_2$をユニタリ行列としたとき、$(U_1 U_2)^\dagger = U_2^\dagger U_1^\dagger$ が成り立つ
- ユニタリ行列の行列式は、絶対値が$1$となる。すなわち、$e^{i\theta}$の形で表せる
複素数ベクトル$\mathbf{x}, \mathbf{y}$の内積$\langle\mathbf{x}, \mathbf{y}\rangle$は、$\mathbf{x}^\dagger \mathbf{y}$ に等しい
- $\langle\mathbf{y}, \mathbf{x}\rangle = \langle\mathbf{x}, \mathbf{y}\rangle^*$が成り立つ。実数ベクトルでは、内積は対称的であったが、複素数ベクトルでは少し異なる
- $A$を行列としたとき、$\langle\mathbf{x}, A\mathbf{y}\rangle = \langle A^\dagger\mathbf{x}, \mathbf{y}\rangle$が成り立つ

ブラケット記法

ブラケット記法は、ベクトルの記法のひとつである。

通常の縦ベクトルを$|x\rangle$のように表記し、ケットと呼ぶ。
$|x\rangle$のエルミート共役を$\langle x|$と表記し、ブラと呼ぶ。すなわち、ブラは横ベクトルである。
内積は、ブラとケットの積で表すが、$\langle x|$と$|y \rangle$の積を$\langle x||y \rangle$ではなく$\langle x|y \rangle$と表記する。$A$を行列としたとき、$\langle x|A|y \rangle$は、横ベクトル$\langle x|$と縦ベクトル$A|y \rangle$の積であり、すなわち、$\langle x|A = (A^\dagger |x\rangle)^\dagger$と$|y \rangle$の積に等しい。
また、$|\langle x|y\rangle|^2 = \langle x|y\rangle^ * \langle x|y\rangle = \langle y|x \rangle \langle x|y \rangle$ が成り立つ。

$|x\rangle = \sum_i^n x_i |i\rangle, |y\rangle = \sum_j^m y_j |j\rangle$のとき、$|x\rangle \langle y|$ は$n\times m$の行列$(x_i y_j^* |i\rangle\langle j|)_{ij}$である。

量子コンピュータ

量子コンピュータとは、以下に述べるような量子ビットを持ち、以下に述べるような操作を高速に行うことができる計算機である¹。それらは、量子回路として図示することができる。

量子ビット

量子ビットとは、その状態をノルムが1の2次元の複素数ベクトルで表すことができ、また、後に述べるような操作が行える量子力学的な物理系のことである。$n$個の量子ビットの状態は、ノルムが1の$2^n$次元の複素数ベクトルで表すことができる。また、量子ビットのような量子力学的な状態のことを量子状態と呼ぶ。
この記事では、具体的な物理系については取り上げない。

実際の量子コンピュータにおいては、量子状態を直接得ることは出来ない。かわりに、何度も同じ量子回路を実行し、その結果をサンプリングすることで、その量子回路の実行結果の分布や期待値を知ることができる。
また、通常のコンピュータで量子状態を追跡することにより量子回路の実行をシミュレーションすれば、量子状態は直接知ることができる。しかし、$n$量子ビットの量子状態は$2^n$次元の複素ベクトルであるため、$n$がある程度大きい場合、量子状態は膨大な空間である。そのため、量子ビットが多数の量子回路は、シミュレーションを行うことが不可能あるいは難しい。²

計算基底

以下で定義する $\{|0\rangle, |1\rangle\}$ は、計算基底と呼ばれている。計算基底は正規直交基底である。
$$\begin{align*}
|0\rangle & = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \\
|1\rangle & = \begin{pmatrix} 0 \\ 1 \end{pmatrix}
\end{align*}$$
量子回路を実行する際、量子状態は、各量子ビットが $|0\rangle$ で表される状態に初期化されている。
すなわち、量子ビットのインデックスをケットの右下に注釈して書くと、$|0\rangle_0\otimes\cdots\otimes|0\rangle_{n-1}$の状態に初期化されている。以後、特に曖昧性がない場合は、量子ビットのインデックスやケットの間の$\otimes$を略記して書く。

量子回路

量子回路とは、量子ビットに対する演算を表す図式である。
横線が量子ビットであり、左から右に向かって、書かれている演算を行うことを示す。

演算は、量子ビットに対して、特定のユニタリ行列を掛ける操作と、量子ビットが計算基底のうちどちらの状態であるかを決定して得る測定とがある。

1量子ビットに対する演算

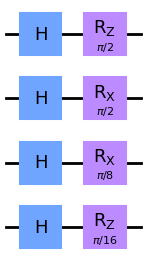
任意の$2\times 2$のユニタリ行列は、(定数倍の違いを除いて)以下のユニタリ行列の積として書き表すことが出来る。ここで、$\theta \in \mathbb{R}$はパラメータとする。

$$\begin{align*}
RX(\theta) & = \begin{pmatrix} \cos \frac{\theta}{2} & -i\sin \frac{\theta}{2} \\ -i\sin \frac{\theta}{2} & \cos \frac{\theta}{2} \end{pmatrix} \\
RY(\theta) & = \begin{pmatrix} \cos \frac{\theta}{2} & -\sin \frac{\theta}{2} \\ \sin \frac{\theta}{2} & \cos \frac{\theta}{2} \end{pmatrix} \\
RZ(\theta) & = \begin{pmatrix} e^{-i\frac{\theta}{2}} & 0 \\ 0 & e^{i\frac{\theta}{2}}\end{pmatrix} \\
\end{align*}$$

また、これらのエルミート共役は、

$$\begin{align*}
RX(\theta)^\dagger &= RX(-\theta) = \begin{pmatrix} \cos \frac{\theta}{2} & i\sin \frac{\theta}{2} \\ i\sin \frac{\theta}{2} & \cos \frac{\theta}{2} \end{pmatrix} \\
RY(\theta)^\dagger &= RY(-\theta) = \begin{pmatrix} \cos \frac{\theta}{2} & \sin \frac{\theta}{2} \\ -\sin \frac{\theta}{2} & \cos \frac{\theta}{2} \end{pmatrix} \\
RZ(\theta)^\dagger &= RZ(-\theta) = \begin{pmatrix} e^{i\frac{\theta}{2}} & 0 \\ 0 & e^{-i\frac{\theta}{2}}\end{pmatrix} \\
\end{align*}$$

である。

また、計算基底を別の正規直交基底に写すために以下がよく用いられる。

$$
H = H^\dagger = \frac{1}{\sqrt 2}\begin{pmatrix}1 & 1 \\ 1 & -1
\end{pmatrix} = e^{i\frac{3}{2}\pi}RZ(\frac{\pi}{2})RX(\frac{\pi}{2})RZ(\frac{\pi}{2})$$

これらのユニタリ行列は、量子ビットに対して作用させることができる。量子状態$|\psi\rangle$があったとき、$i$番目の量子ビットに$2\times 2$のユニタリ行列$U$を作用させたとき、量子状態は

$$(\underbrace{I\otimes\cdots \otimes I}_ {i}\otimes U\otimes\underbrace{I\otimes\cdots \otimes I}_ {n - i - 1})|\psi\rangle$$

に変化する。ただし、$I$は$2\times 2$の単位行列である。量子回路では、このような1量子ビットに対するユニタリ行列の適用を、以下のように四角と文字で図示する。

2量子ビットに対する演算

2量子ビットに対し、以下のユニタリ行列を考える。

$$\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0
\end{pmatrix}$$

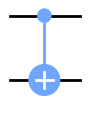
このユニタリ行列の作用を、以下の量子回路で表す。

このユニタリ行列の作用は、$\bullet$ で表された量子ビット(制御量子ビット)が$|1\rangle$のときだけ、 $\oplus$ で表された量子ビット(標的量子ビット)の計算基底の$|0\rangle$と$|1\rangle$を入れ替えるものと捉えることができ、制御NOT(Controlled-NOT)あるいはCNOTやCXと呼ばれている。

測定

以下に定める$P_0, P_1$は、それぞれ$|0\rangle, |1\rangle$への射影である。

$$\begin{align*}
P_0 & = \begin{pmatrix} 1 & 0 \\ 0 & 0\end{pmatrix} =|0\rangle\langle 0| \\
P_1 & = \begin{pmatrix} 0 & 0 \\ 0 & 1\end{pmatrix} =|1\rangle\langle 1|
\end{align*}$$

また、$n$量子ビットからなる量子状態$|\psi\rangle$の$i$番目の量子ビットを測定すると、確率

$$\langle\psi|(\underbrace{I\otimes\cdots \otimes I}_ {i}\otimes P_0\otimes\underbrace{I\otimes\cdots \otimes I}_ {n - i - 1})|\psi\rangle$$
で0が得られ、確率
$$\langle\psi|(\underbrace{I\otimes\cdots \otimes I}_ {i}\otimes P_1\otimes\underbrace{I\otimes\cdots \otimes I}_ {n - i - 1})|\psi\rangle$$
で1が得られる。

$n$量子ビットからなる量子状態$|\psi\rangle$のすべての量子ビットを測定した場合に、得られる値について考える。

$$|\psi\rangle = \sum_{(b_0, \cdots, b_{n-1})\in \{0, 1\}^n} a_{b_0, \cdots, b_{n-1}}|b_0\rangle\cdots|b_{n-1}\rangle$$

のように計算基底で展開すると、$0, \cdots, n-1$番目の量子ビットを測定した値が$b_0, \cdots, b_{n-1} ((b_0, \cdots, b_{n-1})\in \{0, 1\}^n)$となる同時確率は以下のようになる。
$$\begin{align*}
\langle\psi|(P_{b_0}\otimes\cdots\otimes P_{b_{n-1}})|\psi\rangle &= \langle\psi|(|b_0\rangle\langle b_0|\otimes\cdots\otimes|b_{n-1}\rangle\langle b_{n-1}|)|\psi\rangle
\\
&= |(\langle b_0|\cdots\langle b_{n-1}|)|\psi\rangle|^2 \\
&= | \sum_{(b_0', \cdots, b_{n-1}')\in \{0, 1\}^n} \langle b_0|\cdots\langle b_{n-1}|a_{b_0', \cdots, b_{n-1}'}|b_0'\rangle\cdots|b_{n-1}'\rangle|^2 \\
&= |\sum_{(b_0', \cdots, b_{n-1}')\in \{0, 1\}^n} a_{b_0', \cdots, b_{n-1}'}\delta_{b_0', b_0}\cdots\delta_{b_{n-1}', b_{n-1}}|^2 \\
&= |a_{b_0, \cdots, b_{n-1}}|^2
\end{align*}$$

カーネル法

読者は既にカーネル法を知っているものとするため、詳細には述べない。

回帰問題と分類問題

入力データ $x_1, \cdots, x_n \in \mathbb{R}^d$ と、それらに対応する出力データ $y_1, \cdots, y_n$ を考える。$d$は入力データの次元を表す正整数である。
$y_1, \cdots, y_n \in \mathbb{R}$ であり、
$$y \cong f(x)$$
となるような$f$を求める問題を回帰問題という。また、
$y_1, \cdots, y_n \in \{+1, -1\}$ であり、
$$y \cong \mathrm{sign}(f(x))$$
となるような$f$を求める問題を分類問題という。

$f$ が一次関数などの単純すぎる関数の場合、十分に精度のいい$f$を作れないことがあり、また、複雑すぎる関数の場合、過学習を起こすことがある。

カーネルトリック

入力データを写像$\Phi: \mathbb{R}^d \rightarrow X$ により変換した、$\Phi(x_1), \cdots, \Phi(x_n) \in X$と $y_1, \cdots, y_n$ について、一次関数で回帰問題や分類問題を解くことを考える。ここで、$X$は内積を持つ空間とし、特徴空間と呼ぶ。また、$\Phi$を特徴写像と呼ぶ。関数$k: \mathbb{R}^d \times \mathbb{R}^d \rightarrow\mathbb{R}$を、特徴空間上の内積によって、
$$k(x, x') = \langle \Phi(x), \Phi(x')\rangle$$
と定義する。ここでは、このように定められた$k$をカーネルと呼ぶ。

カーネルを用いることで、特徴空間が、どのような空間であるかを知らなくても、

$$K = \begin{pmatrix}
k(x_1, x_1)&\cdots&k(x_1, x_n) \\
\vdots &\ddots & \vdots \\
k(x_n, x_1)&\cdots&k(x_n, x_n)
\end{pmatrix}$$

を使い、回帰問題や分類問題を解くことが出来る(カーネルトリック)。

カーネル

多項式カーネルやRBFカーネルなど、表現力が高いカーネルが経験的に知られている。

量子カーネル法

量子コンピュータは量子回路を高速に実行できること、量子状態は直接得ることが出来ない巨大な空間であることを既に述べた。
そこで、特徴写像の写す先を、量子状態にすることを考える。すなわち、特徴写像$\Phi: \mathbb{R}^d \rightarrow \mathbb{C}^{2^n}$により、入力データ$x$を

$$\Phi(x) = U(x)|0\rangle\cdots|0\rangle$$

のように写す。ここで、$U(x)$は、$x$によって決まるユニタリ行列であり、量子回路としての表し方が既知のものとする。このとき、カーネルは以下のように定まる。

$$k(x, x') = \langle\Phi(x), \Phi(x')\rangle = \langle 0|\cdots\langle 0|U(x)^\dagger U(x')|0\rangle\cdots|0\rangle$$

これは、量子コンピュータで$U(x'), U(x)^\dagger$の操作を行い、量子ビットを測定したときに、全てが0となる確率の平方根に等しい。そのため、量子コンピュータでそのような量子回路を作成し、サンプリングを行うことで、$k(x, x')$の値を得ることが出来る。

特徴写像

上記のような特徴写像は多数考えられるが、その特徴写像によって回帰問題や分類問題などが解けるようなものを選ばなければならない。古典のカーネル法では良い特徴写像が経験的に知られているのに比べ、量子カーネル法では、そういった知見はまだ少ない。

量子カーネル法でよく用いられる特徴写像に、ZZ feature mapがあるため、以下に示す。

この特徴写像だけでは十分な性能が得られないことが多く、パラメータ$\theta$と、別のユニタリ行列$V(\theta)$を用いて、特徴写像を$U(x)V(\theta)$とし、パラメータ探索を行うことが多い。

実装例

Qiskitのチュートリアルに実装例がある。

量子カーネル法の現状と期待

量子カーネル法は、量子コンピュータの特徴とカーネル法の特徴をうまくマッチさせた、面白い手法ではあるが、現時点ではまだ課題が多い。

パラメータ探索なしで求まる経験的に良い特徴写像が知られていないこと
量子コンピュータを用いた場合であっても、量子カーネルの計算は、古典の軽量なカーネルよりは遅いこと
現状は、量子コンピュータのハードウェアが、低精度、小規模、高コストであること

は、特に大きな課題である。

Scholten, Perry II, Washington, et al. (2023)では、テキサス州での鉄砲水の予測に量子カーネル法を使用することが検討された。
郡レベル(N = 2513)、郵便番号レベル(N = 70571)の入力データセットの量子カーネルを計算するのに必要な時間を見積もったところ、郡レベルのデータセットであっても、約1年かかり、実用上は不可能であった。
より最近の量子コンピュータでは、速度が向上しているが、それでも数ヶ月かかる可能性があり、また、郵便番号レベルは依然として処理できないことが述べられている。

一方、量子カーネル法では、古典と比べて過学習しにくいことが理論的に示されているなど、興味深い特徴を持つ。

これらを考慮すると、小規模ながらも従来手法では学習しづらいようなデータが、優位性を発揮しやすいであろう。

まとめ

量子カーネル法の理解のため、量子コンピュータについて述べた。また、量子カーネル法が、量子コンピュータとカーネル法の性質をうまく使った手法であることを見た。現時点では、量子カーネル法は実用的ではないが、小規模なデータを大きな特徴空間に埋め込むことが出来る。

通常のコンピュータのような汎用的な計算も(理論上は)行うことが出来るが、この記事では取り上げない。 ↩
量子回路に使われる操作の種類が限定的であったり、量子回路の横方向の長さが限定的である場合など、量子ビット数が多数であってもシミュレーションが容易になる事例も知られている。また、シミュレーションの精度を下げて近似的にシミュレーションを行う方法なども考えられる。 ↩