はじまり
量子コンピュータアドベントカレンダー1日目では、量子コンピュータとは何なのかについて、見ていきます。
量子アニーリング方式と量子ゲート方式
今現在、世間で「量子コンピュータ」と呼ばれているものには、イジングモデルと呼ばれる問題を解くためのマシンと、量子回路と呼ばれるモデルを実行するためのマシンの2種類があります。
これらは区別せずに語られることも多いですが、別のものと捉えるべきです。前者を「量子アニーリング方式」や「量子アニーラ」、後者を「量子ゲート方式」と呼んで区別することがよくあります。
本アドベントカレンダーでは、量子アニーリング方式も量子ゲート方式も両方とも対象としています。
量子アニーリング方式 (量子アニーラ)とは
量子アニーリング方式のマシンは、組み合わせ最適化問題を解くことに特化しています。(基本的にはそれしかできません)
人によっては、量子アニーリング方式は「量子コンピュータ」に含めるべきではない、と主張している人もいますが、ここではその議論はしません。
必ず最適解にたどり着けるとは限らないですが、多くの問題では、割といい答えを出してくれます。
組み合わせ最適化問題
- Aという条件を満たすようなBの選び方の中で、最もCが小さくなるのは、どんな選び方か?
- 重さWまで入るナップサックがある。重さw1, 価値v1を持つ荷物1、重さw2, 価値v2を持つ荷物2、...、重さwN, 価値vNを持つ荷物Nの中から、ナップサックに入る範囲で、最も価値が高くなるよう荷物を詰めたい。何を選べばいいか?
- Nつの都市がある。これらの都市を、ちょうど各1回ずつ通るルートの中で、最も距離が短いルートはどこか?
- いくつかの図形を箱の中に詰めたい。最も箱の大きさが小さくなる詰め方はどんなものか?
このように、与えられた条件を満たしながら、選べる組み合わせの中から最もいい答えを選ぶ問題を「組み合わせ最適化」と呼んでいます。
こういった問題は、取りうる組み合わせの数が爆発的に増えることが多く、スパコンでも手を付けられないほど難しい問題になってしまうことも珍しくありません。
ある条件の元で何かを選ぶ、という問題は、世の中にありふれており、組み合わせ最適化問題が高速に解けることは、交通、物流、製造業、金融、化学、創薬、その他多くの分野にとって大変うれしいことです。
また、文字通り最適な、最も良い答えを選ぶのが難しかったとしても、割といい答えを手っ取り早く探すことができれば、ビジネス的には御の字です。
貪欲法
組み合わせ最適化問題の、割といい答えを探す方法を考えてみましょう。
例えば、上に挙げたナップサックの問題ですと、価値を重さで割って、「重さあたりの価値」を求めて、重さあたりの価値が高いものから順に詰めていく方法が考えられます。このような方法を貪欲法といいます。
問題によっては、貪欲法で最適な解が求まることもあります。ですが、残念ながら、ナップサック問題は、この方法では最適解から遠い解が得られる場合があります。
この方法は、一見、ベストな選択肢を選んでいるように見えます。ですが、「重さあたりの価値」は高いけど中途半端に重いものを無理に入れるより、諦めて別のを選んだ方がトータルの価値が高くなることもある、ということを見逃しています。
そういった欠点をカバーできる方法はないでしょうか。
焼きなまし法
貪欲法では解けない問題をよりよく解く方法として、昔から広く使われていた方法に、焼きなまし法があります。
これは金属の焼きなましを元にしたものですが、そういう話は置いといて。ざっくりと説明すると、まずはランダムに答えを選んで、そこからさらに、答えの一部を再びランダムに変更します。そのとき、
- 一部を変更した新たな答えが、変える前の答えよりも、良い答えの場合は: 新たな答えを採用する
- 一部を変更した新たな答えよりも、変える前の答えの方が、良い答えの場合は: 「温度」に応じた確率で新たな答えを採用するか、変える前の答えに戻すかを決める
ようにします。徐々に「温度」を下げながら、これを何度か繰り返します。
単に、より良い答えをランダムに探すだけではなく、より悪い答えになっても「温度」に応じた確率で採用するのがポイントで、これにより、損しているように見えてトータルでは得するような選択ができるようになります。
また、「温度」についてですが、温度が高い方が、悪い答えでも採用する確率が高くなります。温度は徐々に下げていくので、最初は悪い答えでも採用する確率が高く、あとの方になると、悪い答えを採用する確率は下がります。
この方法を使っても、最適解が求まる保証はないですが、比較的いい答えが得られるため、広く使われています。
量子アニーリング法
「イジングモデル」と呼ばれる物理モデルを、焼きなまし法を応用した方法で解いたものが量子アニーリングです。(なお、アニーリングとは焼きなましのことです)
イジングモデルや量子アニーリングについてはこちらの記事がおすすめです。
量子アニーリング法が提唱された論文で示されている問題など、一部の問題では、従来の焼きなまし法よりも量子アニーリング法の方がいいようですが、具体的にどういった問題で、量子アニーリングの方が従来の焼きなまし法よりも良いのかについては、現状では、まだ知見は少ないようです。
ノーフリーランチ定理
ノーフリーランチ定理という定理が知られています。
ざっくり言うと、どんな問題にも強い万能の組み合わせ最適化アルゴリズムは存在しない、という定理です。
従来の焼きなまし法も、量子アニーリングも、どちらも何らかの問題に特化していて、決して、どんな問題も解けるとか、どちらかが優れているということはありません。
量子アニーリング方式のマシン
量子アニーリング方式のマシンは、上述の量子アニーリングを、コンピュータシミュレーションではなく、実機で解きます。
「イジングモデル」とは物質と磁場に関する物理モデルなので、実際に物質と磁場を用意すれば、実際に試すことができます。
D-Wave
2018年現在、量子アニーリングを実機で解くマシンは、D-Waveしか選択肢がないと言っても過言ではありません。
ただし、NEDOのプロジェクトで素子の作成を行うとしているので、今後はD-Wave以外のマシンも現れるかもしれません。
また、量子アニーリングの発展とともに、従来の焼きなまし法をするための専用ハードウェアの開発も活発に進んでいることも興味深いです。
特に、マシンによっては「全結合」と呼ばれる、複雑な問題を解くのに都合のよい性質を持っているものも多くあります。また、超伝導が必要ないので極低温にまで冷やさなくてよいことも利点です。
量子アニーリング方式とよく似たマシン
コヒーレントイジングマシン (NTT)
光を使って、イジングモデルを解くためのマシンです。昨年末、「量子ニューラルネットワーク」という名称で発表され、一部の人々の間で話題になりました。
デジタルアニーラ (富士通), CMOSアニーリング (日立)
従来の半導体技術を使って、焼きなまし法でイジングモデルを解くためのマシンです。
量子ゲート方式とは
元々「量子コンピュータ」と呼ばれていたものが量子ゲート方式です。
今のコンピュータは「チューリングマシン」と呼ばれるモデルと等価なものとして知られていますが、量子ゲート方式のマシンは、理論上は、チューリングマシンを拡張した「量子チューリングマシン」と呼ばれるモデルに等価とされています。
量子コンピュータは速いのか?
量子ゲート方式は、まだ実用的な性能を持ったマシンができていないという課題があるのですが。では仮に実用的な性能を持ったマシンがあったとしたら、量子コンピュータは速いのか、という話をします。
量子ゲート方式の量子コンピュータは、暗号を高速に解読するなどの、従来のコンピュータを圧倒的に上回る性能を発揮することが期待されています。
では、どんな問題でも高速になるのでしょうか。従来のプログラムを量子コンピュータで動かすと、何でも高速になるのでしょうか?
それについては、NOです。
量子ゲート方式でできる計算は、万能量子計算とも呼ばれています。
万能ですので、当然、従来のプログラムを量子コンピュータで動かすことも、理論上はできます。
ですが、それらは速くはなりません。
計算量の観点では、量子コンピュータを使っても、従来の計算は、今のコンピュータとさほど変わらない計算量で解けます。
計算量の議論では、マシン自体の速さというのは考慮に入れていなくて、
- 最新のCore i9で計算
- 20年前のCPUで計算
- 人間がプログラムに書いてある手順通りに手作業で計算
のいずれも、区別をしません。
プログラムを1行、計算するのにかかる時間は、三者で全然違うかもしれません。けれど、3つとも同じ手順でプログラムを進めていけば、プログラムが終わるまでに計算しないといけない行数は同じはずです。なので、計算量自体は、いずれも変わらない、という結論になります。
これと同様の議論で、量子ゲート方式のマシンでも、従来のコンピュータで実行するのと似たような計算回数で計算ができることが分かっています。
(もちろん、プログラム1行といっても、大変な行もあれば、楽な行もあります。また、プログラムの行と、従来のコンピュータや量子ゲート方式のマシンで行える計算が1対1で対応しているわけではないのですが、そこらへんはどんぶり勘定しています)
では、1回1回の計算にかかる時間はどうでしょう。実際に実用的なマシンが無い以上、分かりようがないのですが、少なくとも今の量子ゲートの計算にかかる時間については、大体見積もることができます。arXiv:1511.03316 [quant-ph] R. Barends, et al.のFIG. S3.を見てみましょう。いくつか図が載ってますが、FIG. S3. eを引用します。
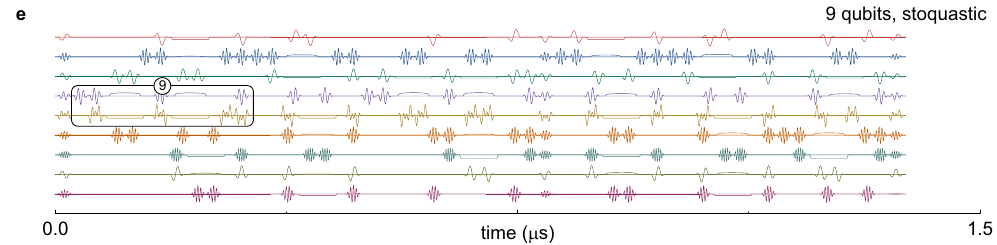
変なにょろにょろが並んでいます。現在主流の超伝導量子ビットは、マイクロ波のパルスを使って量子ビットを制御します。にょろにょろはマイクロ波パルスを表していて、オーダーとしては、1.4マイクロ秒くらい(?)に実行できる操作の数は、ここに載ってるにょろにょろの数だと考えることができます。
ご家庭で使われているIntelのCPUは、恐らく3GHz程度のクロック周波数でしょうから、単純計算で0.3ナノ秒に1つの操作を行えます。つまり、1.2マイクロ秒だと4000操作くらい行えます。
上図に、4000個のパルスが入っているでしょうか? 入っていないですね。
なので、仮に現在の制御方法と全く同じ方法で、理想的なマシンができたと仮定したら、通常の計算は従来のコンピュータよりも遅い、ということになります。
鋭い方なら「けれど、Intel CPUの1クロックでできる計算と、量子ゲート方式で1ゲートでできる計算は対応していないのでは」と考えられるかもしれません。ですが、残念ながら、従来のコンピュータの動作を真似るという目的においては、そのことを考慮すると、量子ゲート方式はさらに遅いことになると思われます。
今後、このパルスが小さくなるかについてですが、パルスの幅はハードウェアの都合で決まっているので、将来のハードウェアがどうなるかに大きく依存します。(あるいは、今の超伝導量子ビットと異なる方式では、こういったパルス制御ではないかもしれません)
逆に、ハードウェアが従来のものから大きく変わらない限りは、パルスの幅も大きくは変わらないでしょう。
量子コンピュータが速いって、どういうことなのか?
上では、仮に今のハードウェアで実用的な量子コンピュータが出来上がったとしても、量子コンピュータで従来の問題を解かせても遅い、ということを見てきました。
では、量子コンピュータは速い、という話は何だったのでしょうか?
実は、にょろにょろのパルスで行われる計算は、従来のコンピュータで計算するには、膨大なメモリを必要し、また、非常に時間がかかる複雑な計算です。
先ほど確認した「速くない」という話は、このような複雑な計算を使って、従来のコンピュータでもすぐにできる計算を行ったら、速くない、という話でした。
ですが、もし、従来のコンピュータでは難しい、複雑な計算を利用して、従来のコンピュータよりも少ない計算回数で答えを求められたとすれば、話はかなり変わってきます。
また、量子コンピュータのビット数が増えれば増えるほど、量子コンピュータでの計算1つ分の計算は、従来のコンピュータで再現するには指数関数的に大変なものになっていきます。
この特徴を生かすことができれば、計算量のオーダーを減らすことができ、従来のコンピュータとは比べ物にならない速度で問題を解くことができます。
実際、一部の問題では、量子ゲートをうまく組み合わせることで、従来のコンピュータよりも少ない計算量で計算ができることが分かっていて、そのような操作の手順を「量子アルゴリズム」と呼びます。
そういった量子アルゴリズムで有名なものに、素因数分解が高速に解けるShorのアルゴリズム、規則性のない配列から特定の値を高速に探し出せるGroverのアルゴリズムなどがあります。
計算量についてざっくりと
コンピュータで高速に計算したいと考える人は、計算量の「オーダー」というものを大変気にします。
例えば、長さがNの配列があったとします。この中から、特定の値を探し出したいとき、配列の並び順に規則性がなければ、ひとつひとつ見ていくしかなく、平均でN/2回、配列の中身を見て、探している値かどうかを確かめる計算が必要になります。N/2回の計算が必要なので、計算にかかる時間は、配列Nの長さに比例します。このような、Nに比例する計算量のオーダーをO(N)と表現します。
ところで、もし配列が、予めソートされていたとしたらどうでしょう。この場合、ひとつひとつ見ていく必要はなく、まずは真ん中を見て半分に絞って、さらに、その真ん中を取って、を繰り返すと、圧倒的に速く値を探すことができます。このように、毎回半分になっていく計算では、配列の長さNに対して、log Nに比例した計算量で計算できることが知られています。つまり、O(log N)と表現し、これはO(N)よりも非常に小さい計算量として知られています。
Nの長さが非常に長くなって、例えば1000倍になったとしましょう。O(N)の計算量では、Nが1000倍になれば、計算にかかる時間は1000倍になってしまい、非常に厳しいのですが、O(log N)の場合は、Nが1000倍になっても、たった10倍程度にしかなりません。このように、計算量のオーダーが下がると、今まではできなかった巨大な計算が高速に解けるようになります。
なお、量子コンピュータを使えば、従来のコンピュータでは、どうしてもO(N)かかっていた、規則性のない配列から値を探す計算が、残念ながらO(log N)にはならないのですが、O(√N)でできることが知られています。この場合、Nが1000倍になっても約30倍の計算時間で計算が行えます。
つまり、量子コンピュータの速さとは
ゲート方式の量子コンピュータの速さについて見ていきました。まとめると、
- 全ての処理が速くなるわけではない
- 1秒間に行える計算の回数は、量子コンピュータは別に多くない
- 従来のコンピュータと同じことを同じ方法でやらせたら、従来のコンピュータの方が速い
- 量子計算の性質を上手に使った「量子アルゴリズム」を使えば高速になりうる
- 計算量のオーダーを小さくすることができれば、計算は高速化し、従来不可能だった計算ができるようになる
- Shorのアルゴリズム、Groverのアルゴリズムなど、既に見つかっている量子アルゴリズムもある
となります。
ハードウェアの課題
ゲート方式の量子コンピュータは、まだハードウェアが未熟です。
規模とノイズの2点がよく課題として挙げられます。
規模(量子ビット数)
2018年12月現在、一般の人が使える量子コンピュータでは、IBMのIBM Q 14 Melbourneの14量子ビットが最多と思われます。
また、Googleが2018年3月に発表した72量子ビットのBristleconeが現状、量子ビット数が最多の量子ゲート方式の実機ですが、詳細な情報は外部にはあまり出ていません。
量子ビット数が少ないと何が問題なのか?
従来のCPUでは、高性能なIntelのものでも64ビットです。マイコンだと、16ビット、8ビットだって、まだまだ現役です。
量子コンピュータは、このビット数だと役に立たないのでしょうか?
CPUのビット数とは、一般には、一度に計算できるデータの大きさを言います。通常は複数のレジスタを持ち、レジスタを操作しながら計算をします。レジスタに入り切らない場合、メモリを使います。
量子コンピュータの場合は、従来のCPUのような複数のレジスタやメモリはありません。量子ビット数と同じ大きさのレジスタが1本あるのみで、他に量子ビットを置く場所はありません。
量子コンピュータ上の量子ビットは、従来のメモリには載せられません。量子ビットを移して保存したり、取り出したりができる、「量子メモリ」というものも研究はされていますが、まだ実用化には至っていない状況です。
つまり、今の量子ゲート式コンピュータには、72量子ビット分のデータしか、そもそも載らないわけです。
それだけしか入力できず、また、それだけしか出力もできません。さらに、途中計算に量子ビットが必要な場合、その分、入出力も減ります。
また、量子ゲート式コンピュータでやっている計算を従来のコンピュータでやると、量子ビット数に応じて指数関数的に大変になることを先に述べました。これは逆に言えば、量子ビットが少ないと、従来のコンピュータでも計算に手間がかからず、量子コンピュータのメリットが少ないということにもなります。
では、何量子ビット欲しいのか
例えば、量子コンピュータの応用例として、素因数分解が期待されています。素因数分解に使うアルゴリズムでは、解きたい問題を2進数で入力し、さらに計算用に問題と同サイズの量子ビットを使います。
今ある72量子ビットのマシンでできる、36ビット整数の素因数分解は、市販のパソコンでもできるサイズで、わざわざ量子コンピュータでする意義がありません。
RSAという暗号で使われる合成数の素因数分解は1024ビットとか2048ビットで、そのためには2048量子ビットや4096量子ビットの量子コンピュータが必要になります。
次に述べる誤り訂正に必要な量子ビットも考えると、さらにあと数桁欲しいです。
ノイズ
量子ビットは、外部からの干渉に非常に弱く、時間とともに量子状態は失われていきます。また、各操作の失敗確率も数%くらいあります。
そういった状況では、時間がかかったり、操作の回数が多いような、複雑な量子アルゴリズムは、現実的には利用できません。
ですが、幸いにも、量子誤り訂正符号という技術があります。
従来のコンピュータでも、DVDやBlu-ray、QRコードなんかにも、誤り訂正符号が記録されており、多少はデータが壊れても読み込めるようになっていることをご存知の方も多いかもしれません。
量子ビットにも、量子誤り訂正符号という技術で誤り訂正ができることが分かっています。
ですが、問題があって、今の実機は誤りが非常に多いため、これを訂正しようとすると、膨大な数の量子ビットを使って1つの量子ビットを表現することになります。
上述の通り、量子ビット数の制約も大きいため、現状は、実用的な誤り訂正は難しいと言えるでしょう。
NISQの時代
2018年1月に、「NISQ」という言葉が生まれました。
NISQとは「Noisy Intermediate-Scale Quantum」の略で、ノイズの多い(誤り訂正ができない)中規模の(50くらいから。スパコンを使っても量子ゲート方式のシミュレーションが難しくなる程度の規模)量子ゲート方式コンピュータを指します。
これからの量子ゲート方式は、NISQの時代に入っていくと考えられ、現状作れるマシンで社会的に意義のある計算が行えるかは現状では未知数ですが、それでも、現状あるもので何かやっていこうという流れは確実に来ています。
VQE
VQEやその仲間(QAOAなど)はNISQを代表する量子アルゴリズムといえます。
ですが、量子アルゴリズムと捉えるよりも、従来のコンピュータに量子コンピュータを付け加えただけ、と捉えた方が、分かりやすいでしょう。
VQEを端的に言うと、量子コンピュータを「パラメータ(このパラメータを変えると、量子コンピュータが行う計算が変わります)を入力すると何か出力が出てくるブラックボックス」として扱って、ブラックボックスからの出力を最小化するよう、(従来のコンピュータで)パラメータの探索を行うアルゴリズムです。
量子化学などの分野で、変分法という計算が知られています。
これは、行列の「固有値問題」と呼ばれる問題を数値的に解く方法のひとつです。
行列には、「固有値」と「固有ベクトル」というものがあることが知られており、これを求めることは物理化学の計算などで非常に重要とされていますが、行列が大きくなると効率的に解くことができません。
「変分法」は、固有ベクトルの候補となる関数をパラメータ調整し、最小化することで、固有値を求めるアプローチですが、そのための行列計算を量子コンピュータにさせます。
これでできることは意外と多く、組み合わせ最適化問題を解くために使えるほか、似た方法による機械学習も提案されています。
最後に
量子コンピュータアドベントカレンダー初日は、量子コンピュータとは何かについて見ていきました。
量子コンピュータは理解が難しく、それゆえ「よく分からないけど、とにかく速い」という雑な認識を持たれがちです。
非常にとっつきづらい分野ですが、従来のコンピュータ科学をきちんと理解されている方なら、十分理解できる、大変夢のある面白い分野です。
それでは、2日目以降もお楽しみください。
