元号が平成か令和かを判定する量子回路組んでみた

平成も終わりですね

令和の時代がやってきます。

昭和に古典コンピュータが生まれ、平成でインターネットとともに普及し、令和は量子コンピュータの時代かもしれません。
もしかしたらその次の元号かもしれませんが、そのような不敬なことは言わず、令和を信じましょう。

令和判定回路

元号が変わると、当然ながら、元号を判定するプログラムが必要になります。
量子コンピュータで元号判定をする必要があるかどうかは現時点では定かではありませんが、きっと必要となるでしょう。だって令和だから。

ということで、西暦と月を入れると、令和かそうじゃないかを判定する回路を作っていきましょう。
シミュレータで動かす都合上、ビット数を少なくするため、西暦2000年〜2031年に限定しています。

アルゴリズム概要

令和というと和ですね。加算回路を使ってみましょう。

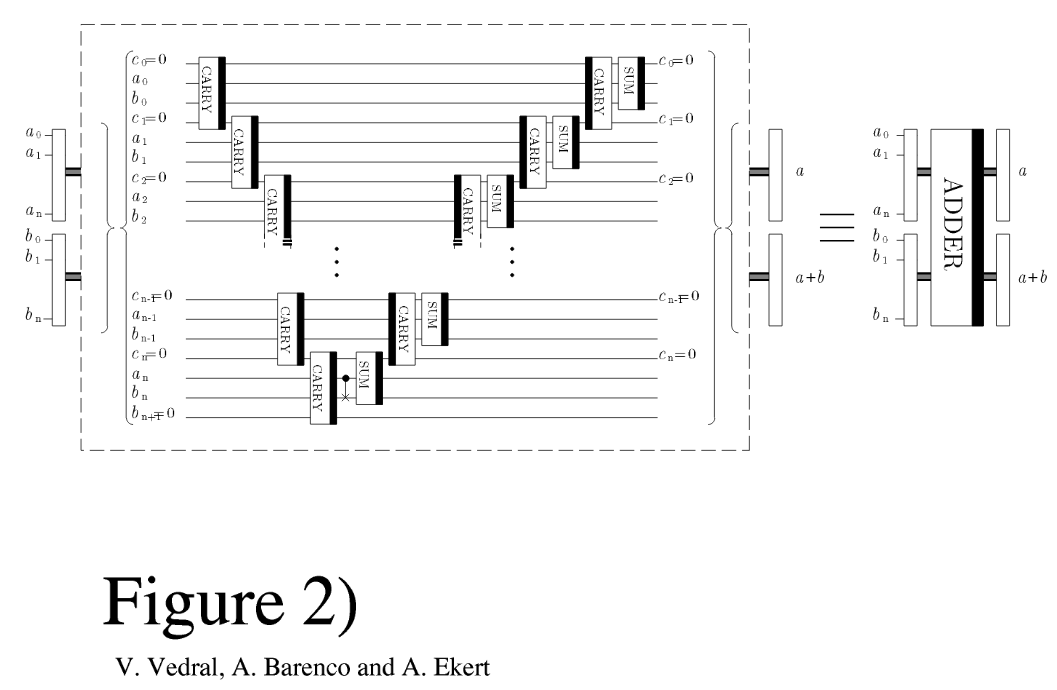
https://arxiv.org/pdf/quant-ph/9511018.pdf のFigure 2に加算回路が載っています。これは、
|a>|b>|0> → |a>|a+b>|0>
の計算をするための回路です。

量子回路の世界では、観測をしない限りは、すべての演算は逆演算が可能となっています。
逆演算をするには、大雑把には、回路を逆向けに通します。¹

逆演算すると
|a>|a+b>|0> → |a>|b>|0>
となり、これはつまり
|a>|b>|0> → |a>|b-a>|0>
をしています。

20yy年mm月を、yymmという数字だと考えましょう。
元号が変わるのが2019年05月なので、yymmから1905を引くと²、令和だと非負に、平成だと負の数になります。
整数が負か非負かの判定は、量子回路でも非常に簡単で、最上位ビットが立っていたら負、立っていなかったら非負と考えることができます。
(この考え方は、通常のコンピュータにおける整数演算と全く同様です)

つまり、最上位ビットを観測すれば、令和か平成かが分かるわけですね。

さらに今回、もっとビット数を節約したいですね。aは定数(1905)なので、使わない回路に書き換えます。加算回路にはCNOTとToffoliゲートしか使われておらず、また、|a>はそれらの制御ビットとしてしか利用されていないので、|a>のビットが0ならばCNOT, Toffoliゲートは消して、1ならばCNOTはXに、ToffoliはCNOTに変換できます。

これらを最新版のBlueqatで実装してみました。

回路の実装

from blueqat import Circuit, BlueqatGlobalSetting

def sum0(c, ci, bi):
    return c.cx[ci, bi]

def carry0(c, ci, bi, cj):
    return c.ccx[ci, bi, cj]

def sum1(c, ci, bi):
    return c.x[bi].cx[ci, bi]

def carry1(c, ci, bi, cj):
    return c.cx[bi, cj].x[bi].ccx[ci, bi, cj]

def uncarry1(c, ci, bi, cj):
    return c.ccx[ci, bi, cj].x[bi].cx[bi, cj]

BlueqatGlobalSetting.register_macro('sum0', sum0)
BlueqatGlobalSetting.register_macro('carry0', carry0)
BlueqatGlobalSetting.register_macro('uncarry0', carry0)
BlueqatGlobalSetting.register_macro('sum1', sum1)
BlueqatGlobalSetting.register_macro('carry1', carry1)
BlueqatGlobalSetting.register_macro('uncarry1', uncarry1)


def unadder(c, a, b0, c0, n_bits):
    a_bits = [(a >> i) & 1 for i in range(n_bits)]
    for i in range(n_bits - 1):
        if a_bits[i]:
            c.sum1(c0 + i, b0 + i).carry1(c0 + i, b0 + i, c0 + i + 1)
        else:
            c.sum0(c0 + i, b0 + i).carry0(c0 + i, b0 + i, c0 + i + 1)
    if a_bits[-1]:
        c.sum1(c0 + n_bits - 1, b0 + n_bits - 1).x[b0 + n_bits - 1]
        c.uncarry1(c0 + n_bits - 1, b0 + n_bits - 1, b0 + n_bits)
    else:
        c.sum0(c0 + n_bits - 1, b0 + n_bits - 1)
        c.uncarry0(c0 + n_bits - 1, b0 + n_bits - 1, b0 + n_bits)
    for i in reversed(range(n_bits - 1)):
        if a_bits[i]:
            c.uncarry1(c0 + i, b0 + i, c0 + i + 1)
        else:
            c.uncarry0(c0 + i, b0 + i, c0 + i + 1)
    return c


BlueqatGlobalSetting.register_macro('unadder', unadder)

def set_(c, val, pos):
    def g(val):
        i = 0
        while val:
            if val & 1:
                yield pos + i
            i += 1
            val >>= 1
    return c.x[tuple(g(val))]

BlueqatGlobalSetting.register_macro('set', set_)

def is_reiwa(year, month):
    n_bits = 9
    pos_month = 0
    pos_year = 4
    pos_result = 9
    pos_ancilla = 10
    count = Circuit().set(year - 2000, pos_year) \
                     .set(month, pos_month) \
                     .unadder(((2019 - 2000) << pos_year) | 5, pos_month, pos_ancilla, n_bits) \
                     .m[pos_result] \
                     .run(shots=1)
    return '1' not in count.most_common(1)[0][0]

for year, month in [
        (2016, 9), (2017, 10), (2018, 11), (2018, 12),
        (2019, 3), (2019, 4), (2019, 5), (2019, 6),
        (2020, 1), (2020, 2), (2022, 3), (2023, 4)]:
    print(f'is_reiwa({year}, {month}) => {is_reiwa(year, month)}')

実行結果はこうです。

is_reiwa(2016, 9) => False
is_reiwa(2017, 10) => False
is_reiwa(2018, 11) => False
is_reiwa(2018, 12) => False
is_reiwa(2019, 3) => False
is_reiwa(2019, 4) => False
is_reiwa(2019, 5) => True
is_reiwa(2019, 6) => True
is_reiwa(2020, 1) => True
is_reiwa(2020, 2) => True
is_reiwa(2022, 3) => True
is_reiwa(2023, 4) => True

どやっ！

Blueqatのマクロ機能

今回、最新版Blueqatに搭載されたマクロ機能を多用してみました。
これは、BlueqatのCircuitを引数に取る関数をマクロとして登録すると、Circuitのメソッド呼び出しとして使えるようになる機能です。

単に関数呼び出しをメソッドの形にしているだけなので、これがないとできない機能とかは無いのですが、Blueqatの特徴であるメソッドチェーンがさらにやりやすくなりました。

例えば、上でも定義している、setマクロはなかなか有用ではないかと思います。

def set_(c, val, pos):
    def g(val):
        i = 0
        while val:
            if val & 1:
                yield pos + i
            i += 1
            val >>= 1
    return c.x[tuple(g(val))]

BlueqatGlobalSetting.register_macro('set', set_)

これは

print(Circuit().set(6, 0).run(shots=1))

のように使い、この場合は、0ビット目を最下位ビットとして、整数の6を(Xゲートを使って)回路にセットします。

つまり、

---
-X-
-X-

のような回路が作られます。

Blueqatについて

Blueqatはオープンソースの量子コンピュータライブラリで、とにかく手軽で使いやすいのが特徴です。
今のところ、主に私が開発していますが、オープンソースですので、開発を手伝ってくれる仲間も募集中です。

また、使ってもらえたり、GitHubでスターをいただけると、とても嬉しいです。

平成に終わりを告げるライブラリ、初春の令月にして気淑く風和ぐライブラリ、Blueqatをよろしくお願いします。

1. 今回の回路ではそれでいけますが、一般には、逆にするだけでなく、各ゲートのエルミート共役をとる必要があります。量子コンピュータに使われるゲートはすべてユニタリ行列で、ゲートを並べるとユニタリ行列の積になります。つまり、各ゲートを$U_1, U_2, \dots, U_n$とすれば$(U_1 U_2 \dots U_n) (U_1 U_2 \dots U_n)^\dagger = I$の関係になっているため、$U_1 U_2 \dots U_n$の逆演算は $(U_1 U_2 \dots U_n)^\dagger = U_n^\dagger \dots U_2^\dagger U_1^\dagger$ のようになります) ↩

2. 本当はこれを2進数でやる、つまり、月は4ビットで表現して、 0x13 << 4 | 0x05 = 0x1305を引きます。が、説明めんどいので、以降も1905と書きます。 ↩