筆者は統計学初心者のため、内容の正しさは保証できません。本記事の内容をまじめな用途で使われる際はご注意ください。また、間違いの指摘やよりよい方法、関連して知っておくとよいことなどがありましたら、コメントいただけると幸いです。
降水確率は当たるのか?
確率ってのは、数え上げて割り算すれば求められる。けれど、降水確率となると。同じ日は二度と来ないし、降水確率は日によって変わる。果たして、降水確率というものは、どこまで信頼できるのだろうか。適当に数字を出しているだけではないだろうか。
降水確率が90%でも、雨が降らない日はある。100%ではないのだから、おかしくはない。けれど「100%じゃないから雨じゃなくても間違いではありません」では、何の意味もない。降水確率90%の晴れの日は、本当に降水確率90%だったのだろうか。
例えばもし、降水確率が毎日30%なら、妥当性は検証できる。
もし、降水確率が毎日同じならば、毎日、晴れたか雨だったかを記録し、雨だった日を数えれば、降水確率は検証できる。二項検定か、カイ二乗検定などで求められる。
降水確率として出てくる数字が有限個で、その個数がサンプル数に比べて少なければ、求まるのではないか。
さらには、滅多に出ない珍しい降水確率が存在しないか、あったとしても、それを考慮しても十分にサンプル数があるという仮定も欲しいが。ともかく、有限個で、サンプル数が十分にあれば「この降水確率が予報された日は、何パーセントの確率で雨が降る」というデータが作れる。
そして、気象庁が発表している降水確率は、実は0%から100%までの10%刻みと決まっている。この方法が使えそうだ。(もしそのようになっていなくても、10%刻みにデータを区分けして強引にこのようにする方法だってある)
降水確率の定義
気象庁の予報用語のページより引用。
a)予報区内で一定の時間内に降水量にして1mm以上の雨または雪の降る確率(%)の平均値で、0、10、20、…、100%で表現する(この間は四捨五入する)。
b)降水確率30%とは、30%という予報が100回発表されたとき、その内のおよそ30回は1mm以上の降水があるという意味であり、降水量を予報するものではない。 降水確率は、予報区内で一定の時間内に1mm以上の雨または雪(融けたときの降水量に換算する)が降る確率であり、0%から100%まで10%刻みの値で発表される。
これにも注意した方がよさそうだ。
対象時間は、短期予報は6時間、週間予報では24時間とする。
なんと、今日の天気の欄に出る短期の降水確率と、週間予報の欄に出る1日の降水確率は、定義が違っていたのだ。前者は6時間の間に1mm以上降る確率で、24時間の間に1mm以上降る確率ということだ。知らなかった。
気象庁の過去データ
http://www.data.jma.go.jp/obd/stats/etrn/ で過去の気象データの閲覧が、
http://www.data.jma.go.jp/gmd/risk/obsdl/index.php でダウンロードができる。
タダでこんなの公開してくれてるなんて、こりゃありがたい。
1日あたりの降水量を得ることができた。
ただ、残念ながら、予報した降水確率は公開されていないようだ。
降水確率の過去データ
こちらのWebページで、東京の過去の天気予報を(個人の方が?)公開されている。
http://homepage3.nifty.com/i_sawaki/WeatherForecast/
すごい・・・・
データは揃った。やってみよう
とりあえず、上述のサイトから、2014年1月1日~2014年12月31日までのデータを集めてみた。
降水確率は、1日の降水確率の中では最も新しい、2日前の値を使用した。
的中具合を定量的に表すには?
それぞれの降水確率の妥当性は、カイ二乗検定などでも分かるが、全体としてどうなんだ、というのを求めたい。そのために、今回は「決定係数」というものを使ってみた。
Wikipediaによると、定義には諸説あるようだが、一般的、とされている
$R^2 = 1-\frac{\Sigma_i(y_i-f_i)^2}{\Sigma_i(y_i-\overline{y})^2}$
を使用した。
決定係数は回帰曲線の当てはまりのよさを見るのに使われ、数値が大きいほど当てはまりがいいと言え、最大で1になる。また、この定義では、マイナスの値にもなりうる。
今回のは回帰曲線とは違うが、
($x_i$, $y_i$) = (予報降水確率, その予報のときの降雨日数/その予報が出た日数)
とし、また、推定値は、 $f_i = x_i$とした。
Python(2でも3でも動くはず)で書いたコードをこのあたりに掲載している。
2014年の降水確率の的中具合は?
ここに示したのが、2014年の降水確率の分布だ。
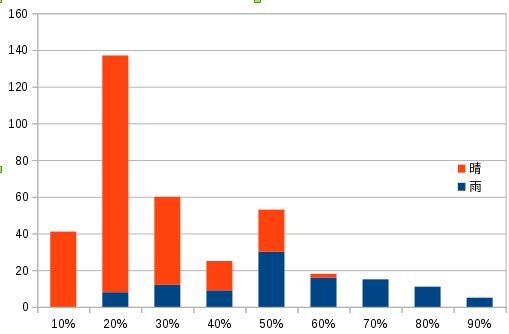
横軸を降水確率の予報、縦軸を、その予報のときの降雨日数/その予報が出た日数ととったのがこちら。

このときの決定係数の値は 0.8714 となった。
「決定係数 目安」などで検索すると、特にいくら以上だといいといった基準はないらしいが、0.5以上だと十分によい回帰であるようだ。0.8714は、なかなかにいい値なのではないだろうか。
無事に、降水確率はデタラメではないことが分かった。