QAOAとVQE
QAOA(Quantum Approximate Optimization Algorithm)は、量子ゲート方式の量子コンピュータを使ってイジングモデルを最適化するアルゴリズムです。また、VQE(Variational Quantum Eigensolver)は、量子ゲート方式の量子コンピュータを使って行列の固有値を求めるアルゴリズムで、量子化学計算などによく使われます。
誤り訂正のない量子コンピュータでもそこそこ動くので、近年、QAOAやVQEの開発が盛んに進められています。
量子コンピュータのライブラリのレベルで見ると、QAOAはVQEの一種として扱われていることが多く、Blueqatでも、QAOAはVQEの一種として扱っています。
VQE/QAOAで解きたい問題
ハミルトニアンと呼ばれる行列$\hat H$が与えられます。この行列に対し、ノルム1のベクトルであって、$\boldsymbol{X}\cdot \hat H \boldsymbol{X}$ (ただし$\cdot$は内積)が最小になるような$\boldsymbol{X}$を探したとき、$\boldsymbol{X}\cdot \hat H \boldsymbol{X}$の値はいくらか、という問題をVQE/QAOAによって解くことができます。
ハミルトニアンの形や問題を解く目的によって、QAOAと呼ばれたりVQEと呼ばれたりします。
また、$\boldsymbol{X}\cdot \hat H \boldsymbol{X}$は「エネルギー」とも呼ばれます。量子力学では、実際にこれがエネルギーを求める式に相当するためです。
これが効率よく解けると
- ある種の最適化問題はこの形に落とし込むことができるので、最適化問題を解くために使える
- QAOAは、モチベーションとしてはこちらに近い
- このような$\boldsymbol{X}$は行列$\hat H$の固有ベクトルであり、$\boldsymbol{X}\cdot \hat H \boldsymbol{X}$は$\hat H$の最小の固有値であることが知られているので、いわゆる固有値問題を解くのに使える
- VQEは、モチベーションとしてはこちらに近い
- 量子化学などでは、固有値問題を解けると非常に嬉しい
- エネルギーが最小となる電子配置を求めることができる
といった応用があります。
VQEの大まかな流れ
量子コンピュータは、巨大な行列を作って、量子ビットと呼ばれるベクトルに掛け算して、その結果できる確率分布にしたがってビット列をサンプリングするのが得意です。
量子コンピュータは、大雑把には、量子ゲートを組み合わせて作られる「量子回路」を動かす装置です。量子回路を渡すと、ビット列をサンプリングしてくれます。
ビット列のサンプリング結果から$\boldsymbol{X}\cdot \hat H \boldsymbol{X}$を求めることができるので、少しずつ量子回路を変えながら、量子コンピュータに量子回路を渡していって、$\boldsymbol{X}\cdot \hat H \boldsymbol{X}$を最小にするような量子回路を求めます。
それが求まれば
- $\boldsymbol{X}\cdot \hat H \boldsymbol{X}$の最小値
- $\boldsymbol{X}\cdot \hat H \boldsymbol{X}$が最小になるような$\boldsymbol{X}$の、測定結果(ビット列)の確率分布
を得ることができます。
少しずつ量子回路を変えながら?
量子ゲートには「量子ビットを回転させる」操作に対応するものがあります。
回転させる角度をパラメータとして持たせることで、パラメータに応じた量子回路を作ることができます。
角度は、単なる浮動小数点型の値なので、
パラメータ(浮動小数点型)→量子回路→ビット列のサンプリング結果→エネルギー(浮動小数点型)
といった具合で計算をすることができ、「浮動小数点型を与えれば、浮動小数点型を返す関数」だと考えることができます。
この関数を最小化することで、求めたい結果が得られます。
これらの最適化にはよく、scipy.optimize.minimizeが使われます。また、ベイズ最適化などが使われる場合もあります。
量子コンピュータシミュレータ特有の事情
量子コンピュータの実機では、ビット列をサンプリングによって(何度も同じ量子回路を計算して、結果を何度も取ることで)得ていました。
これは、量子コンピュータの内部状態(状態ベクトル、波動関数などと呼ばれることもあります)をそのまま取り出すことができないためです。
一方で、シミュレータの場合は、内部状態を配列で持っているので、そのまま取り出すことができ、何度も同じ量子回路を計算するよりも効率的にビット列の確率分布を得ることができます。
計算速度だけではなく、計算精度にも効いてくるので、VQEやQAOAの論文を読むときは、シミュレータか実機かを気にすることは非常に重要です。
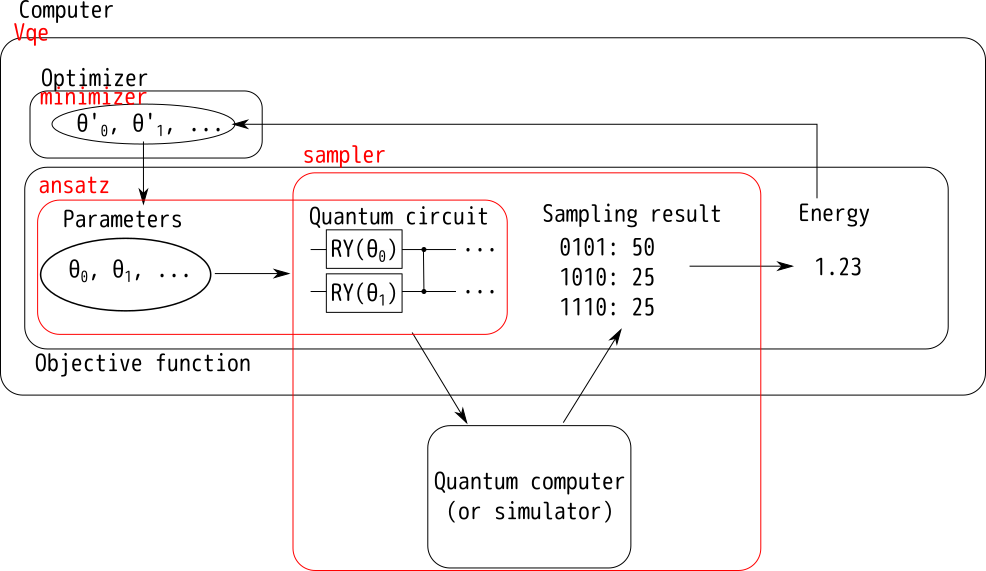
絵にしてみる
Blueqatで書いてみる
QAOAでは、量子アニーリングなどで解かれるイジングモデルと同じように、ZとZZ相互作用と呼ばれるもののみを使って、ハミルトニアンを記述します。
単純なQUBOとして、q(0) - 2 * q(1) - 3 * q(0) * q(1)を考えてみましょう。q(0), q(1)を量子ビットとして、それぞれ、0と1といずれかの値を取ったとき、どの組み合わせのとき、この式は最小になるかを考えます。
2変数だったら、手計算で総当りできて、
q(0) |
q(1) |
q(0) - 2 * q(1) - 3 * q(0) * q(1) |
|---|---|---|
| 0 | 0 | 0 - 20 - 30*0 = 0 |
| 1 | 0 | 1 - 20 - 31*0 = 1 |
| 0 | 1 | 0 - 21 - 30*1 = -2 |
| 1 | 1 | 1 - 21 - 31*1 = -4 |
なので、(1, 1)のとき最小値を取ります。
これを求めるには
from blueqat.pauli import qubo_bit as q
from blueqat.vqe import Vqe, QaoaAnsatz
h = q(0) - 2 * q(1) - 3 * q(0) * q(1)
ansatz = QaoaAnsatz(h, 4) # 2個目の引数は、パラメータや回路をどの程度増やすか。多い方が解ける確率が上がるが、解くのに時間がかかる
runner = Vqe(ansatz)
result = runner.run()
print(result.most_common())
とすればよく、結果は
(((1, 1), 0.944590105656669),)
と、94%以上の確率で(1, 1)が得られました。
ソースを読む
qubo_bit
docstringは省略します。qubo_bitは、単にこうなっています。
def qubo_bit(n):
return 0.5 - 0.5*Z[n]
これは、QUBO($q_i\in\{0, 1\}$)のビットで書かれたものをイジングモデル($\sigma_i\in\{\pm 1\}$)に書き直しているだけです。$q_i = 0$のとき$\sigma_i = 1$に、$q_i = 1$のとき$\sigma_i = -1$になるように計算しています。
Zは、blueqat.pauli内でごちゃごちゃと定義されているのですが、VQEやQAOAに使う際は、
-
Z[i]をそのまま、または、係数や他のZ[i]と掛け算してTerm型に - さらに
Term型を足し算・引き算してExpr型に
して使われます。
また、
-
Expr型はTermのタプルで出来ている -
Term型は、パウリ行列X, Y, Zのタプルと係数(floatかcomplex)でできている-
Term型は「時間発展」と呼ばれる計算を量子回路に付け加えるための関数を用意している
-
という関係になっています。
時間発展は、VQEやQAOAで非常に重要な計算になります。
本当は、ハミルトニアン$\hat H$の時間発展を書けたら嬉しいので、Expr型を時間発展したいのですが、一般にそれをゲートの組み合わせで書くのは難しく、通常は鈴木トロッター展開などによる近似計算が行われます。
一方、掛け算のみからなるTerm型は、ゲートの組み合わせで時間発展が簡単にできます。
QaoaAnsatz.__init__
Ansatzというのは、日本語では「仮設」などと訳されるらしいドイツ語ですが、$\boldsymbol{X}\cdot \hat H \boldsymbol{X}$における$\boldsymbol{X}$の候補のようなもので、VQEでは、$\boldsymbol{X}$の候補となる量子回路をこのように呼ぶことも結構あります。
後で見ますが、QaoaAnsatzで最も重要なメソッドはget_circuit()で、このメソッドは、パラメータから量子回路を作る役割を担います。
class QaoaAnsatz(AnsatzBase):
def __init__(self, hamiltonian, step=1, init_circuit=None):
super().__init__(hamiltonian, step * 2)
self.hamiltonian = hamiltonian.to_expr().simplify()
if not self.check_hamiltonian():
raise ValueError("Hamiltonian terms are not commutable")
self.step = step
self.n_qubits = self.hamiltonian.max_n() + 1
if init_circuit:
self.init_circuit = init_circuit
if init_circuit.n_qubits > self.n_qubits:
self.n_qubits = init_circuit.n_qubits
else:
self.init_circuit = Circuit(self.n_qubits).h[:]
self.init_circuit.make_cache()
self.time_evolutions = [term.get_time_evolution() for term in self.hamiltonian]
# 親クラスの__init__はこちら
class AnsatzBase:
def __init__(self, hamiltonian, n_params):
self.hamiltonian = hamiltonian
self.n_params = n_params
self.n_qubits = self.hamiltonian.max_n() + 1
親クラスの__init__に渡すものとしては、hamiltonian ($\hat H$)と、パラメータ数と、量子ビット数です。
パラメータ数は、ステップ数の倍を渡しています。
さらにhamiltonianを、hamiltonian.to_expr().simplify()で、型を無理矢理Exprに合わせて、さらに、simplify()では余分な項などを削ったりまとめたりしています。
check_hamiltonianでは、QAOAに適したハミルトニアンかをチェックしています。
初期回路として、特に指定がなければ、すべての量子ビットにHをかけたものを渡しています。
これは、量子アニーリングでいうところの、最初に横向けの磁場をかけた状態からアニーリングをはじめることに相当します。
make_cache()を呼ぶと、一部のシミュレータでは、この段階まで量子計算を行い、結果を取っておきます。
これから何度も、初期回路にゲートを付け加えたものを動かすので、このようにしておくことで無駄な計算を減らすことが出来ます。
self.time_evolutions = [term.get_time_evolution() for term in self.hamiltonian]では、Expr型のhamiltonianからTerm型のtermを取り出して、時間発展のための関数を得ます。
Vqe.__init__
class Vqe:
def __init__(self, ansatz, minimizer=None, sampler=None):
self.ansatz = ansatz
self.minimizer = minimizer or get_scipy_minimizer(
method="Powell",
options={"ftol": 5.0e-2, "xtol": 5.0e-2, "maxiter": 1000}
)
self.sampler = sampler or non_sampling_sampler
self._result = None
ansatz, minimizer, samplerの3つのオブジェクトを取ります。
また、minimizer, samplerは省略したらデフォルトのものが使われます。
minimizerは、最小化を行うための関数で、デフォルトでは、scipy.optimize.minimizeをラップしたものが使われます。
samplerは、実機やシミュレータを動かして、サンプリング結果を得るための関数で、デフォルトではシミュレータを使います。
先ほどの図に、これらを書き入れると、以下のようになります。
図がややこしくなるので省略しましたが、サンプリング結果からエネルギーを求めるのもansatzがやっています。(エネルギー計算にhamiltonianが必要になるため、hamiltonianを持っているオブジェクトにやらせています)
Vqe.run()
def run(self, verbose=False):
objective = self.ansatz.get_objective(self.sampler)
if verbose:
def verbose_objective(objective):
def f(params):
val = objective(params)
print("params:", params, "val:", val)
return val
return f
objective = verbose_objective(objective)
params = self.minimizer(objective, self.ansatz.n_params)
c = self.ansatz.get_circuit(params)
return VqeResult(self, params, c)
if verbose:以下は、パラメータやエネルギー変化を見たい人用にごちゃごちゃ出すようにしているだけなので、あまり気にしなくて良くて、それを無視したら
-
get_objective(sampler)で目的関数を得る -
minimizerを呼び出して、目的関数の値を最小化する - 最小化の結果得られたパラメータから回路を作り、結果を出す
というシンプルな処理になっています。
get_objective
def get_objective(self, sampler):
"""Get an objective function to be optimized."""
def objective(params):
circuit = self.get_circuit(params)
circuit.make_cache()
return self.get_energy(circuit, sampler)
return objective
目的関数は、まさに図でやっているとおり、
- パラメータ
paramsを受け取って、量子回路を作る - 量子回路を
samplerで動かしてエネルギーを得る
という流れになっています。
このようにして得られた目的関数について、minimizerによってパラメータを最適化するので、本当に図の通りの動きをしていることが分かりました。
まとめ
VQE, QAOAは、流れさえ把握できれば、決して複雑なアルゴリズムではありません。
今回は、実際にどういう流れで動いているのかをソースを読みながら図に書き入れてみました。
おまけ: 今のBlueqatのVQEモジュールの問題点
できるだけ疎結合になるように、できるだけ子クラスに権限委譲するように、モジュールを作っていました。
けれど、VQEの鍵は「いかにしてパラメータの最適化を行うか」であって、特に化学計算では、初期値に分子構造から求まるパラメータを用いてもいいし、使えるものは何でも使って最適化を行いたいのです。
それは、今のVQEモジュールの構造とは非常に相性が悪い考えです。
現状、minimizerは、どんな関数を最適化するのかについて、関数そのものとパラメータ数以外、何の情報も与えられていません。関数の中味はブラックボックスとして最適化をしています。
どのようにモジュールを組み直したら、より良い最適化ができるでしょう?
(今のところ、minimizerを外部から渡すのではなく、Vqeオブジェクトを継承し、メソッドとして生やしてはどうかと考えています)
また、samplerとのやりとりにも問題があります。
現在のsamplerでは、回路はひとつひとつ動かすことを想定していましたが、実はIBM Qでは、複数の回路を詰め込んでクラウド上の量子コンピュータに投げることができるのです。
IBM Qでは、計算時間よりも順番待ちの時間の方が長い、ということが常態化しており、複数の回路を詰め込んで実行できることは大幅な時間の節約につながります。
では、どうやったら、複数の回路を詰め込めるような構造にできるでしょう?
(単に回路のリストを受け取ったら、まとめて実行して、結果のリストを返す、とかでいい気はしています)
Blueqatは、クソややこしい量子計算についての悩みよりもむしろ、こういう、ソフトウェア開発あるあるの悩みをいっぱい抱えています。
オープンソースのソフトウェアなので、開発に協力してくれる人を探しています。腕に自信のある方は、ぜひ、お声掛けください。