ZZ相互作用の行列とその時間発展回路を真面目に説明してみる

ZZ相互作用の行列はVQEやQAOAなどに頻繁に使われているのに、真面目に説明している記事が意外とない気がしたので、ちゃんと説明してみます。

イジングモデルのZZ相互作用の項

イジングモデルでは、各ビットが+1または-1のどちらかの値を取ります。
例えば、$1.23 s_1 s_2$だと、

$s_1$	$s_2$	$1.23 s_1 s_2$
+1	+1	+1.23
+1	-1	-1.23
-1	+1	-1.23
-1	-1	+1.23

のようになり、最適化問題では、これらの項をもっといっぱい足し算したものが最小値を取るようにsを選ぶことになります。

パウリのZ行列

パウリのZ行列と呼ばれる行列があります。

$\sigma^{(z)} = \begin{pmatrix}1 & 0 \\ 0 & -1\end{pmatrix}$

量子力学的には、イジングモデルは、この行列を状態ベクトルに作用したものと考えます。
どういうことかというと、

1量子ビットの場合

$$|0> = \begin{pmatrix}1 \\ 0 \end{pmatrix}$$
$$|1> = \begin{pmatrix}0 \\ 1 \end{pmatrix}$$

とおくと、

\begin{eqnarray}\sigma^{(z)}|0> &=& \begin{pmatrix}1 & 0 \\ 0 & -1\end{pmatrix}\begin{pmatrix}1 \\ 0 \end{pmatrix}\\ &=& \begin{pmatrix}1 \\ 0 \end{pmatrix}\\& = & |0>\\ \\
\sigma^{(z)}|1> &=& \begin{pmatrix}1 & 0 \\ 0 & -1\end{pmatrix}\begin{pmatrix}0 \\ 1 \end{pmatrix}\\ &=& \begin{pmatrix}0 \\ -1 \end{pmatrix}\\& = & -|1>
\end{eqnarray}

|0>に$\sigma^{(z)}$を掛けると+1倍、|1>に$\sigma^{(z)}$を掛けると-1倍になっていることが重要です。
この+1, -1が、イジングモデルに出てくる+1, -1に対応します。

2量子ビットの場合

|00>, |01>, |10>, |11>がそれぞれ
$\begin{pmatrix}1\\0\\0\\0\end{pmatrix}, \begin{pmatrix}0\\1\\0\\0\end{pmatrix}, \begin{pmatrix}0\\0\\1\\0\end{pmatrix}, \begin{pmatrix}0\\0\\0\\1\end{pmatrix}$
に対応します。
文献によっては|10>と|01>が逆になっていますが、単にビットを読む順番の問題で、特に大きな違いはありません。

$\sigma^{(z)}$が2個の場合、

\begin{eqnarray}
\sigma^{(z)}\otimes\sigma^{(z)}&=&\begin{pmatrix}1Z & 0Z \\ 0Z & -Z\end{pmatrix}\\
&=&\begin{pmatrix}Z & O \\ O & -Z\end{pmatrix}\\
&=&\begin{pmatrix}1&0 & 0&0 \\ 0&-1 & 0&0 \\ 0&0 & -1&0 \\ 0&0 & 0&1\end{pmatrix}\\
\end{eqnarray}

($O$は2x2の、全部がゼロの行列)
のように、ひとつずつ行列を展開して、大きな行列を作ります。

実は|00>, ..., |11>も同じように作っているので、余裕ある人はやってみてください。

また、$\sigma^{(z)}\otimes\sigma^{(z)}|00>$, ..., $\sigma^{(z)}\otimes\sigma^{(z)}|11>$を計算してみると、|00>, |11>のときに+1, |10>, |01>のときに-1になります。|0>が+1, |1>が-1になることを思い出すと、これらの掛け算になっていることも確認できます。

ZZ相互作用の時間発展

ZZ相互作用をQAOAやVQEで書くとき、「時間発展」の形にするのが普通です。
時間発展に関する詳しい説明は避けますが、行列を指数関数の肩に載せた

\exp(i\sigma^{(z)}\otimes\sigma^{(z)}t)

のような形になります。
ここで注意すべきは、この$\exp$は行列指数関数といい、

\exp(A) = \sum_{n=0}^{\infty}\frac{A^n}{n!}

の形をしています。一般には、numpyなどで計算するときは、np.exp(A)では計算できないことに注意してください。(np.expを使うと、単に行列の各成分に指数関数を適用します。これは上式とは別物です)
かわりにscipy.linalg.expmを使うと、行列指数関数を計算することができます。

行列指数関数は、無限に行列積をとらないといけないため、直接計算するのは非常に困難で、行列を対角化してから求めるのが簡単です。

一方、対角行列では、行列指数関数を取るのは簡単で、単に各成分に指数関数を適用したものになります。(つまり、対角行列の時は、np.expで計算したものと一致します)
$\sigma^{(z)}\otimes\sigma^{(z)}$は対角行列なので、$\exp(i\sigma^{(z)}\otimes\sigma^{(z)}t)$を求めてみると、

\begin{eqnarray}
\exp(i\sigma^{(z)}\otimes\sigma^{(z)}t) &=& \exp \left( i \begin{pmatrix}1&0 & 0&0 \\ 0&-1 & 0&0 \\ 0&0 & -1&0 \\ 0&0 & 0&1\end{pmatrix} t \right) \\
&=&\exp \left( \begin{pmatrix}it&0 & 0&0 \\ 0&-it & 0&0 \\ 0&0 & -it&0 \\ 0&0 & 0&it\end{pmatrix}\right) \\
&=&\begin{pmatrix}e^{it}&0 & 0&0 \\ 0&e^{-it} & 0&0 \\ 0&0 & e^{-it}&0 \\ 0&0 & 0&e^{it}\end{pmatrix}
\end{eqnarray}

となります。これを量子回路で作ってみます。

ZZ相互作用を時間発展させる量子回路

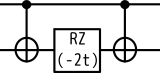
天下り式ですが、これは

の回路で作ることができます。
ひとつひとつ見ていきます。

RZの前後に挟まっているCNOTゲートは

$CNOT = \begin{pmatrix}
1&0&0&0\\
0&1&0&0\\
0&0&0&1\\
0&0&1&0\end{pmatrix}$

でした。
また、RZゲートは

$RZ(\theta) = \begin{pmatrix}
e^{-i\theta / 2} &0\\
0&e^{i\theta / 2}\end{pmatrix}$

でした。2つの量子ビットのうち、下のビットにかけているので、以下のような形に直しておいた方がいいでしょう。

$\begin{eqnarray}
I\otimes RZ(\theta) &=& \begin{pmatrix}1 RZ(\theta) & 0 RZ(\theta) \\ 0 RZ(\theta) & 1 RZ(\theta) \end{pmatrix}\\
&=& \begin{pmatrix}RZ(\theta) & O \\ O&RZ(\theta) \end{pmatrix}\\
&=& \begin{pmatrix}e^{-i\theta / 2} &0&0&0\\
0&e^{i\theta / 2}&0&0\\
0&0&e^{-i\theta / 2} &0\\
0&0&0&e^{i\theta / 2}
\end{pmatrix}
\end{eqnarray}
$

これを計算していくと、

\begin{eqnarray}
&&CNOT \cdot I\otimes RZ(\theta) \cdot CNOT\\ &=& \begin{pmatrix}
1&0&0&0\\
0&1&0&0\\
0&0&0&1\\
0&0&1&0\end{pmatrix}\begin{pmatrix}e^{-i\theta / 2} &0&0&0\\
0&e^{i\theta / 2}&0&0\\
0&0&e^{-i\theta / 2} &0\\
0&0&0&e^{i\theta / 2}
 \end{pmatrix} \begin{pmatrix}
1&0&0&0\\
0&1&0&0\\
0&0&0&1\\
0&0&1&0\end{pmatrix} \\
&=&
\begin{pmatrix}e^{-i\theta / 2} &0&0&0\\
0&e^{i\theta / 2}&0&0\\
0&0 &0&e^{i\theta / 2}\\
0&0&e^{-i\theta / 2}&0
 \end{pmatrix} \begin{pmatrix}
1&0&0&0\\
0&1&0&0\\
0&0&0&1\\
0&0&1&0\end{pmatrix}\\
&=&\begin{pmatrix}e^{-i\theta / 2} &0&0&0\\
0&e^{i\theta / 2}&0&0\\
0&0 &e^{i\theta / 2}&0\\
0&0&0&e^{-i\theta / 2}
 \end{pmatrix}
\end{eqnarray}

となります。ここで、$\theta = -2t$を代入すると、

\begin{eqnarray}
&&CNOT \cdot I\otimes RZ(-2t) \cdot CNOT\\ &=& \begin{pmatrix}e^{it} &0&0&0\\
0&e^{-it}&0&0\\
0&0 &e^{-it}&0\\
0&0&0&e^{it}
 \end{pmatrix}\\
&=&\exp(i\sigma^{(z)}\otimes\sigma^{(z)}t)
\end{eqnarray}

と、ZZ相互作用の時間発展が作れました。

まとめ

本記事では、ZZ相互作用とその時間発展についての説明と、量子回路作りを行いました。
VQEやQAOAの基本となる部分ですので、そのあたりに興味のある方は、知っておくといいかと思います。