こういうのを、TwitterやらFacebookやらで見たことがないでしょうか。

これは私がでっち上げたものですが。検索すれば、いくつか見つかります。
**これ、どうやって作ってんの!?**って疑問が湧いてきたので、ちょっと考えてみました。
コードは全部、Python3で実装しています。2.xを使っている方は日本語を使うことが多いなら乗り換えましょう。入り口と出口でだけ文字コードに注意すれば、unicodeだとかcodecだとかなーんにも気にしなくていいので、とても楽ちんです。
戦略1: 完全にランダムでひらがなを選ぶ
import random
h, w = 16, 16
USE_HIRAGANAS = ('あいうえおかきくけこさしすせそたちつてと' +
'なにぬねのはひふへほまみむめもやゆよらりるれろわん' +
'がぎぐげござじずぜぞだぢづでどばびぶべぼぱぴぷぺぽ')
for _ in range(h):
print(''.join(random.choice(USE_HIRAGANAS) for _ in range(w)))
るづるぽぬづぢぢらぬよあうどぺぽ
げよじなめひけぺえのぱつめあぼう
づこぽざざごぎばぼらひわちろゆぶ
すごめうへされぬさかたてすきぴち
んめじかばれねわぼるきすぴびびな
のうぴほみにれぜうなざもむおぼつ
ろぶざほぽざえしぷさちしおこよむ
なとはござえことどめつせぴぞづそ
のなめすなやしむらしたもがこぞに
んてぱべそゆすぴびはへんんへあた
めばとへちながけもけやすづむほは
やぶどそえわへにさぢやのもぼぬぬ
まびろごずるるゆぴるぢわわづもさ
がぜとそづまほあおさぢげづはめき
ちこしげてびきねぼぺざずぼはねね
たせやするこへとだつなしくわしき
単語が見つかる気がしないです。残念。
戦略2: ひらがなの出現頻度を考慮し、よく使われるひらがなを高い確率で選ぶ。
オープンソースな日本語入力システムの辞書として使われているcannadic改の、gcanna.ctdを、ひらがな文字列のサンプルとして使いました。
ちなみに、各ひらがなの出現頻度はこんな感じでした。
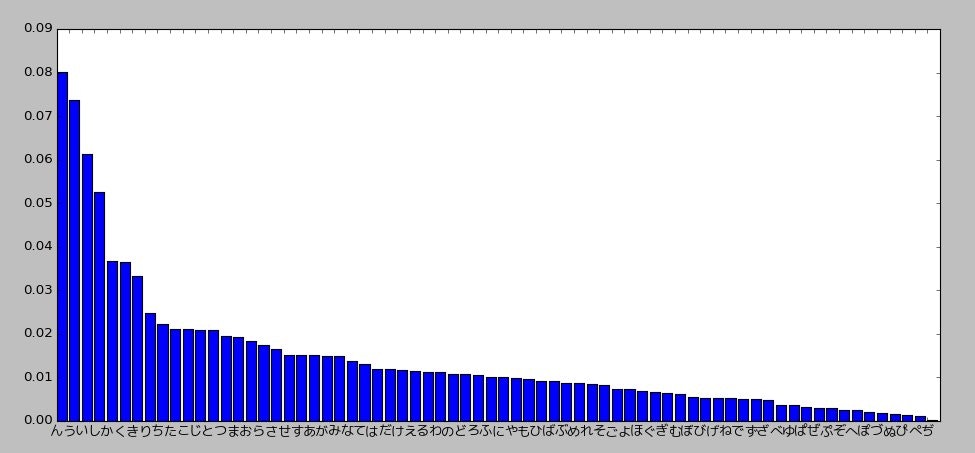
(matplotlibで日本語をとうふにならないよう表示させる方法についてはこちらを参考にしました)
確率の高いひらがなを選びやすくするコード例は、こんな感じです。
def make_text1(hist, height, width):
n = sum(hist.values())
keyvalues = hist.most_common()
a = [keyvalues[0][1]]
for x in keyvalues[1:]:
a.append(a[-1] + x[1])
def _get():
x = random.randrange(n)
for i,y in enumerate(a):
if x < y:
return keyvalues[i][0]
return '\n'.join([''.join([_get() for _ in range(width)])
for _ in range(height)])
ちなみに、histは、collections.Counter型を想定しています。
dict型のサブクラスで、使い勝手としては、defaultdict(lambda:0)と似ていますが、
Counter型同士で足し算をしたり、Counter.most_common()で、数の多い順に((key, value), ...)を得られたりできて、大変便利です。
そして、結果、こんなひらがなの羅列が得られました。
きごらえしららつおうせんんいうた
みごだこてあずちうかりごのうくり
ぶぶちどなちんけふいおだこしこふ
ゆぎたどがんしらんのてうみいいと
めさげんあきでびうろひろろいいに
んはたぶいくううすきらしくるざう
ふうわんろさひうたはうじみかくぼ
ちつけんめざんいうこまかんしうき
じりよじちんとぱるぎこのそがうか
どりんごなけなおいいちたしやちほ
とうせださらごはさだむうもむしん
ふぞきせぞりくききさちあいくかふ
りううちのさとんどしついとまわち
ちいらうたふせすまびみぜしれこそ
そはちしちんししくびくみはいけき
んなばこんうしたほぎきくうこあん
かなりよくなりました。かなりマシです。これなら探す気力が湧いてきます。
けれど、もうすこしよくならないでしょうか。
戦略3: あるひらがなから、別のひらがなへの遷移確率を考慮に入れる
要は、1階のマルコフ過程ですね。
コードを抜粋して示します。
ちなみにmarkovは、collections.defaultdict(collections.Counter)となっていて、markov['あ']['い']は、「あ」の次が「い」であった数を数えています。本来は、確率になるように、各要素をsum(markov['あ'].values())で割り算しないといけないけど、サボっていたので、この関数でそれもやっています。
def tee(func, arg):
func(arg)
return arg
def make_text2(markov, hist, height, width):
'''次にくるひらがなも考慮した、ひらがなの羅列。'''
def _get(up, left):
'''上の文字からの遷移と左の文字からの遷移を考える'''
c = norm_markov[up] + norm_markov[left]
x = random.random() * 2.0
y = 0.0
for k,v in c.most_common():
y += v
if x <= y:
#print('_get:', up, left, '-->', k)
return k
# 上の文字、左の文字からの遷移を考えるので、0列目の前の列、0行目の前の行が
# 必要になるが、便宜上、ひらがなの出現頻度から作った行を使用する。
firstcol = make_text1(hist, 1, width)
prevline = make_text1(hist, 1, width).strip()
#print('firstcol', firstcol)
#print('prevline', prevline)
# markovを正規化する。
# 上の文字からの遷移と左の文字からの遷移のウェイトを同じにするため。
norm_markov = {}
for k1,cnt in markov.items():
c = Counter()
n = sum(cnt.values())
for k2,v in cnt.items():
c[k2] = v / n
norm_markov[k1] = c
a = []
for i in range(height):
line = []
functools.reduce(lambda x,j: tee(line.append, _get(prevline[j], x)),
range(width), firstcol[i])
a.append(''.join(line))
prevline = line
return '\n'.join(a)
ちなみに、markovを作るのは、こんな感じのコードでいけます。(だいぶ省略してます)
from collections import deque
from collections import defaultdict
from collections import Counter
def shiftiter(iterable, n):
'''Generator which yields iterable[0:n], iterable[1:n+1], ...
Example: shiftiter(range(5), 3) yields (0, 1, 2), (1, 2, 3), (2, 3, 4)'''
# I used deque, but I'm not sure it is fastest way:(
it = iter(iterable)
try:
a = deque([next(it) for _ in range(n)])
yield tuple(a)
except StopIteration:
pass
for x in it:
a.popleft()
a.append(x)
yield tuple(a)
USE_HIRAGANAS = ('あいうえおかきくけこさしすせそたちつてと' +
'なにぬねのはひふへほまみむめもやゆよらりるれろわん' +
'がぎぐげござじずぜぞだぢづでどばびぶべぼぱぴぷぺぽ')
markov = defaultdict(Counter)
with open(FILENAME, encoding=FILEENCODING) as f:
for line in f:
hiragana = line.split()[0]
for x,y in shiftiter(hiragana, 2):
if x in USE_HIRAGANAS and y in USE_HIRAGANAS:
markov[x][y] += 1
結果、こんな感じになりました。
きせついげじんかとんたさいきごせ
ちいしずんらくいおつびしきめぶい
がしあにかほういしんようれるさと
んとるすてきめすどうほれてぎんん
るいがほうこきねうしんいつごうり
けほわうんねごるえぎぱいいとうし
んでんららしいすいせうちあなたし
さんけだいちちとはかこりいちんざ
にぎんいおもとよいへうりこうちせ
んれごかせんかふぬやしんくそうか
けんはむめきめんしろかしりだきい
なきふなみさいかもいいなやまげか
おろすんたねせんしいすてんきはつ
とうけじいおさんかそんかきおごと
んがやまよしごきほうじまみしずう
びちくじこばりちいちずむこんぐか
これなら探す気になりませんか!
ランダムなので、何度か作って、割とできのいいのを選ばないとダメな印象ではありますが、
なかなか悪くないです。
まだ満足しない人のための、今後の検討事項
2階あるいはさらに高階のマルコフ過程
やってみるといいかもしれないですね。
文字の選び方
現状、確率分布を大きい方から累積して、0〜1に正規化して、0〜1の乱数で選ぶ、みたいな処理をしています。(実際はちょっと違いますが、意味としてはだいたいそんな感じ)
でも、1%の確率でしか出現しないひらがなを、1%の確率で選ばないといけないのか?無視してはいけないのか?とは思います。
ですが、80%くらいまでしか選ばれないように改造してみたところ「ん」とか「う」とかの、頻度の高いひらがなが大量に選ばれてしまいました。頻度が高い側についても、何らかの調整が必要なようです。
コードはgithub
興味を持っていただけた方へ: コードはgithubに上げています。
https://github.com/gyu-don/jikken/tree/master/markov
ライセンス表示(GPL)をするのが面倒だったので、gcanna.ctdはアップロードしていませんが、集計済みデータを出力したものをアップロードしていますので、なくても実行できます。(もし今回のコードをGPLで使いたい方がいらっしゃいましたら、使って頂いて問題ありませんが)
gcanna.ctdはこちらからダウンロードできます。
https://osdn.jp/projects/alt-cannadic/releases/