TL;DR
- 【単タイプじゃんけん】 はがね、ドラゴン、みずの三タイプがTop tier。次点はゴースト、じめん、フェアリー。
- 【複数タイプじゃんけん】 一番選択したほうがいいタイプはくさ+いわ(ポケモンではユレイドル系統の固有タイプ)。ガブリアスでお馴染みのじめん+ドラゴンはこの分析でも強かった。
- 【テラスタルじゃんけん】 一番選択したほうがいいタイプはノーマル(ゴーストテラスタル)。はがねテラスタルカイリュー(ひこう+ドラゴン)はこの分析でも強かった。
- テラスタルなしの場合、最弱はむしとどく。選択しても負けやすくなるだけ。ただしテラスタルありなら全タイプに活躍の機会がある。
ポケモンとタイプ相性
ポケモンは言わずと知れた人気ゲームですが、ことポケモン対戦において必ず考慮しなければならないものの一つにタイプ相性があります。くさはみずに強く、みずはほのおに強く、ほのおはくさに強いといった関係ですね。
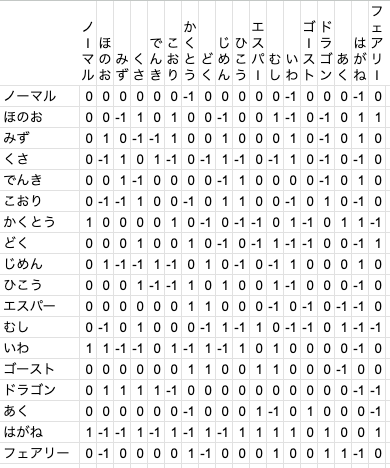
ポケモンの世界では現時点で18種類のタイプが確認されており、これらのタイプ間には次の相性があることがわかっています:

(詳細は公式サイトを参照。)
この図を見ると各タイプごとに△や◯の数が全然違うことがわかりますよね。例えばエスパータイプは2タイプしか△がない(半減にできない)一方、はがねタイプは11タイプで△(半減)もしくは×(無効)になっています。こういう偏りに気づくと実はタイプ間に上下関係があるのではないか?強いては最強のタイプが存在するのではないか?という疑問が生まれてきます。
そこでこの記事ではその疑問に答えるためにポケモンのタイプでじゃんけんするケースを考え、その想定下における最強のタイプをゲーム理論の観点から考察していきます。
前置き: 通常のじゃんけんに最強手はある?
いきなり18タイプを考える前にまず通常のじゃんけんについて考えましょう。興味がない方は飛ばしていただいて大丈夫です。
直感的にはじゃんけんに最強手はない気がしますよね。グーチョキパーのどれを出しても勝率は同じな気がします。それではどんな場合でも必ずグーを出すという戦略でいいのでしょうか?実はこの問いの答えはYesでありNoなのです。
仮に相手がグーチョキパーを1/3ずつの確率で繰り出してくる場合、もちろんグーを出せば1/3の確率で勝利することができます。
しかしながらもし相手にこちらの戦略(=必ずグーを出す)がリークしていたとしたらどうでしょうか。相手は必ずパーを出すことで必ずこちらに100%勝利することができてしまうのです。
戦略のリークは非現実的すぎるようにも思えますが、例えば100回連続じゃんけんをするようなケースを考えたら途中で相手はこちらの戦略(=必ずグーを出す)を見抜けそうですよね。このように戦略のリークは発生しうるのです。
では「必ずグーを出す」戦略ではなく「グーチョキパーの中からランダムに直前で選んで出す」という戦略を採用したらどうでしょうか。これなら相手に戦略がリークしようが勝率はちゃんと1/3になりますよね。
このように「選択肢の中から確率的に一つ選んで実行する」戦略をゲーム理論では混合戦略と言い、相手に戦略がリークしている場合に最も高い勝率を達成できる混合戦略を混合戦略のナッシュ均衡と呼びます。
じゃんけんにおける混合戦略のナッシュ均衡
それではじゃんけんにおける混合戦略のナッシュ均衡の求め方を考えてみましょう。
今回は自分も相手も混合戦略を取ってくると想定して考えます。ここでは自分がグー、チョキ、パーを出す確率をそれぞれ$x_1,x_2,x_3$, 相手の確率を$y_1,y_2,y_3$としましょう。また勝つと1ポイント獲得し、負けると1ポイント失うとしましょう(いわゆるゼロサムゲームです)。この場合自分の獲得ポイントの期待値は次の式で表せます:
\textbf{x}^T A \textbf{y},
where\quad A=\begin{pmatrix}
0 & 1 & -1\\
-1 & 0 & 1\\
1 & -1 & 0\\
\end{pmatrix}
今回は自分の混合戦略がリークしていたとしても最高の期待値が出せるような混合戦略を求めてみましょう。自分の混合戦略がリークしていた場合、相手は対抗して最も勝てる混合戦略を選ぶと仮定します。具体的には次を最小化させるyを選択するとします:
\min_{\textbf{y}\in \textrm{S}} \textbf{x}^T A \textbf{y},
where\quad\textrm{S}=\{\textbf{x}|0\le\textbf{x}_i\le1, \sum \textbf{x}_i=1\},
今回はこのyに対して最高の勝率が出せるxを求めたいので、具体的には次の式を最大化するようなxを求めます:
\max_{\textbf{x}\in \textrm{S}} \min_{\textbf{y}\in \textrm{S}} \textbf{x}^T A \textbf{y},
where\quad\textrm{S}=\{\textbf{x}|0\le\textbf{x}_i\le1, \sum \textbf{x}_i=1\},
結果としてシンプルなmin-max問題に落ち着きました。これを解くことで$x_1,x_2,x_3=\frac{1}{3}$という解が得られ、グーチョキパーを平等にランダムに選ぶ混合戦略が最適であるという結論が得られます。この解がいわゆる混合戦略のナッシュ均衡です。
(サラッと解を書きましたが上のmin-max問題は解くのに工夫が必要です。詳しい解き方は補足欄に飛ばしますがご興味があればぜひ。)
以上で前置きは終わりです。以降ではここまでのアプローチを利用して肝心のポケモンのタイプじゃんけんの最強戦略を考察していきます。
タイプじゃんけんの最強戦略: 単タイプ編
ここから本題であるポケモンのタイプじゃんけんの最強戦略について考察していきます。
二つのタイプ間の勝敗ですが今回はタイプ間のダメージ倍率の比率に基づいて決定しましょう。具体的にはタイプiからjのダメージ倍率を$r_{i{\rightarrow}j}$として、次の式$s_{i{\rightarrow}j}$が1より大きければ勝ち、1より小さければ負け、1なら引き分けとしましょう。
s_{i{\rightarrow}j} = \frac{r_{i{\rightarrow}j} + \epsilon}{r_{j{\rightarrow}i} + \epsilon}
($\epsilon$は$10^{-10}$など適当に設定したとても小さい数です。ゼロ除算を防ぐために足し合わせます。)
見づらいですが、一応ノーマルがかくとうやいわ、はがねに対して-1ポイントになっていたりするのでテーブル自体は正しそうです。
結果
この勝ち負けポイント行列を使って混合戦略のナッシュ均衡を計算してみましょう。いきなり結果をお見せすると以下の通りです:
[順位] タイプ: 選択確率
[1位] ドラゴン: 0.158
[1位] はがね: 0.158
[1位] みず: 0.158
[4位] じめん: 0.105
[4位] でんき: 0.105
[4位] ゴースト: 0.105
[4位] フェアリー: 0.105
[8位] くさ: 0.053
[8位] こおり: 0.053
それ以外: 0
この選択確率に従ってタイプを選択することで相手がどんな戦略を取ろうが勝ち負けポイントの期待値が必ず0以上になります。また、選択確率が大きいほど高頻度に出したほうがいいことになるので、選択確率は一種の強さの指数とも考えられます。
以下に軽く感想を書きます:
- 選択確率のトップはドラゴンとはがねとみずでした。
- ドラゴンとはがねが最高位なのはガチ勢の方々にとってもイメージ通りなのではないでしょうか。ポケモンSVの四天王にもはがね使い(ポピー)とドラゴン使い(ハッサク)がいますが、このデータからも納得のいく人選なのでオモダカさんの慧眼たるや。
- 加えてみずがトップに来ているのが面白いです。タイプ相性の観点では御三家最強はみずタイプということになります。では対戦環境だとウェーニバルが御三家ポケモンで最も使用率が高いかというと全くそんなことない、というか一番低い(2023/03時点)のがポケモン対戦の奥深いところですよね。
- この三タイプの次にはでんき、ゴースト、フェアリー、じめん、くさ、こおりの六タイプが続きました。
- フェアリーは最強タイプのドラゴンの攻撃を無効化できるのが強そうですね。
- じめんといえばポケモンSVのチリちゃんですよね。オモダカさんの慧眼たるや(2回目)。
- でんきは弱点がじめんタイプの一種類しかないことが有名です。この順位も納得です。ナンジャモをすこれ。
- 御三家からくさが8位にランクインです。くさタイプは不利対面の多い軟弱タイプ(語弊)という印象がありましたがトップのみずタイプに勝てるタイプでもあります。
- こおりはフェアリー同様ドラゴンタイプの弱点なのでこの順位も納得です。変温動物は低温に弱い。
- それ以外のタイプの選択確率は0です。つまり相性じゃんけんにおいて出さないほうがいいタイプということになります。
- ノーマルは有利を取れるタイプがないので出さないほうがいいのは割と直感通りですよね。加えてむしやエスパーも出さないほうがいいというのはガチ勢の方々なら体感通りではないでしょうか。
- 御三家の中ではほのおタイプは出さないほうがいいという結論になりました...これは上位のドラゴン、みず、じめんへの弱さが効いている可能性が高そうです。
これ以外にもナッシュ均衡になる混合戦略はないの?
今回の問題に関してはあります。
他の均衡点としては例えば次のものがありました:
[1位] ドラゴン: 0.176
[1位] はがね: 0.176
[1位] みず: 0.176
[4位] じめん: 0.118
[4位] ゴースト: 0.118
[4位] フェアリー: 0.118
[7位] くさ: 0.059
[7位] でんき: 0.059
それ以外: 0
手動で解空間を探索してみましたが、どうやらドラゴン、はがね、みずの三タイプがTier1で、ゴースト、フェアリー、じめんがTier2という順序はいつも変わらず、でんきとこおりとくさの順序および各タイプの選択確率だけが変わるようです。
ただしどの戦略を採用してもナッシュ均衡である限り相手の戦略に関わらず勝ち負けポイントの期待値が0以上になります。
タイプじゃんけんの最強戦略: 複数タイプ編
ここまではポケモンのタイプ数は一つだと想定して話を進めてきましたが、多くの方が知る通りポケモンにはタイプを二つ持つものがいます。次は複数タイプも考慮に入れた相性じゃんけんを考えてみましょう。
複数タイプの相性の計算法
複数タイプのポケモン同士の相性の決定には少し工夫が必要です。例えば次の例を考えてみましょう1:
- マスカーニャ: くさ+あく
- ウェーニバル: みず+かくとう
草は水に強い一方で格闘は悪に強いんですよね。ということは二体とも相手の弱点をつけるということになります。そう考えるとこの二体は相性的には同程度と考えられそうですよね。
もう一つ例を考えてみましょう:
- カイリュー: ドラゴン+ひこう
- ユキノオー: こおり+くさ
ひこうはくさの弱点なのでカイリューはユキノオーの弱点をつくことができます。一方でこおりタイプはドラゴン、ひこうの両方の弱点になっています。この場合こおりタイプは四倍弱点になるのでカイリューにとって極めて大きな弱点ということになります。この対面はユキノオーのほうが相性的に有利そうですよね。
そこで今回は複数タイプ間の勝敗は与えられうるダメージ倍率の最大値の比率に基づいて決定することにしましょう。具体的にはタイプiから(k+l)のダメージ倍率を$r_{i{\rightarrow}jk}$として、次の式$s_{ij{\rightarrow}kl}$が1より大きければ勝ち、1より小さければ負け、1なら引き分けとしましょう。
s_{ij{\rightarrow}kl} = \frac{\max{(r_{i{\rightarrow}kl}, r_{j{\rightarrow}kl})} + \epsilon}{\max{(r_{k{\rightarrow}ij}, r_{l{\rightarrow}ij})} + \epsilon}
($\epsilon$はとても小さい数でゼロ除算を防ぐために足し合わせています。)
この場合の勝ち負けポイント行列は次のようになります:
読めるわけがない!w 一応組合せの多さはわかりやすいのでこのテーブルは消さずに残しておくことにしました。実際のテーブルが気になる方はこちらのGoogle sheetをご確認ください。
結果
この勝ち負けポイント行列を使って混合戦略のナッシュ均衡を計算してみましょう。結果は以下の通りです。わかりやすくなるようこのテーブルでは該当するポケモンも載せておきます(最終進化のみ、ポケ徹様調べ):
[順位] タイプ: 選択確率
[1位] くさ+いわ: 0.135 (ユレイドル、岩オーガポン)
[2位] ほのお+じめん: 0.119 (バクーダ、ゲンシグラードン)
[3位] みず+じめん: 0.118 (ガマゲロゲ、ラグラージ、ヌオーなど)
[4位] でんき+ひこう: 0.074 (タイカイデン、サンダー、ボルトロスなど)
[5位] ドラゴン+はがね: 0.067 (ブリジュラス、ディアルガ)
[6位] ひこう+はがね: 0.066 (アーマーガア、エアームド、テッカグヤ)
[7位] くさ+でんき: 0.059 (カットロトム、ヒスイマルマイン)
[8位] ノーマル+ゴースト: 0.046 (ヒスイゾロアーク)
[9位] でんき+フェアリー: 0.034 (カプ・コケコ、デデンネ)
[10位] みず+ひこう: 0.032 (ペリッパー、ギャラドス、ウッウなど)
[11位] かくとう+エスパー: 0.031 (エルレイド、チャーレムなど)
[12位] かくとう+あく: 0.031 (ズルズキン、ゴロンダ、ウーラオス(いちげき))
[13位] みず+こおり: 0.030 (テツノツツミ、ラプラス、パルシェンなど)
[14位] かくとう+フェアリー: 0.030 (テツノブジン)
[15位] じめん+ひこう: 0.030 (グライオン、ランドロスなど)
[16位] じめん+ドラゴン: 0.025 (ガブリアス、フライゴン、ジガルデ)
[17位] ほのお+くさ: 0.024 (スコヴィラン)
[18位] みず+ドラゴン: 0.021 (ウネルミナモ、シャリタツ、キングドラなど)
[19位] でんき+はがね: 0.013 (トゲデマル、ジバコイル)
[20位] くさ+はがね: 0.012 (ナットレイ、カミツルギ)
[21位] こおり+フェアリー: 0.006 (アローラキュウコン)
それ以外: 0
繰り返しになりますがこの選択確率に従ってタイプを選択することで相手がどんな戦略を取ろうが勝ち負けポイントの期待値が必ず0以上になります。また、選択確率が大きいほど高頻度に出したほうがいいことになるので、選択確率は一種の強さの指数とも考えられます。
以下に軽く感想を書きます:
- ナッシュ均衡における選択確率のトップはくさ+いわでした。にわかな自分にとっては予想外でしたが調べると単タイプ相手では7タイプ(ノーマル、ほのお、みず、でんき、じめん、ひこう、いわ)に有利が取れる一方で不利対面は2タイプ(どく、はがね)のみと大変優秀なタイプであることがわかりました。
- 現在の対戦環境でもよくみるポケモンたちがちらほらいます。6位ひこう+はがねのアーマーガアは受けポケモンとして有名ですし、13位みず+こおりのテツノツツミ、14位かくとう+フェアリーのテツノブジン、19位でんき+はがねのジバコイルなんかもランクマ実況動画ではよく見るポケモンです。
- 最も美しい種族値をもつことで知られるガブリアスはドラゴン+じめんタイプですが、この表では15位にランクインしています。種族値だけでなくタイプ相性でも強いのか......
- 単タイプじゃんけんでは出さないほうがいいという結論になっていたタイプもちらほら見られます。特にいわ、ほのお、ひこう、ノーマル、かくとう、エスパー、あくの7タイプは他のタイプと組み合わさることでじゃんけんで出したほうが良いタイプになるようです。
- それ以外のタイプの選択確率は0です。つまり相性じゃんけんにおいて出さないほうがいいタイプということになります。
- どく、むしの二タイプは単タイプじゃんけんだけでなく複数タイプじゃんけんでも現れませんでした。つまりじゃんけんで使ってもいいことがないタイプということができそうです。
- この解析には単タイプも混ぜているんですが一つも見られませんでした。複数タイプの方が打点が豊富で有利を取りやすいということがわかりますね。
なおこの問題についてはこれが唯一のナッシュ均衡になっているようです。
タイプじゃんけんの最強戦略: テラスタル編
ポケモンSVにおけるタイプ相性を語る上でテラスタルは外せないですよね。最後にテラスタル込みでのタイプじゃんけんの最善戦略を考えることにしましょう。
テラスタルって何?
「テラスタル」とは、ポケモンたちが宝石のようにキラキラと光り輝く、パルデア地方特有の現象で、全てのポケモンが「テラスタル」し、特別な力を手に入れることができます。テラスタルすると、頭部などにテラスタルジュエルが王冠のように発生し、体表はカットした宝石のようにきらめきます。その発生には、パルデア地方の地中からにじみ出るテラスタルエネルギーが関係していると言われています。詳しくはわかっていないことが多く、オーリム博士/フトゥー博士がその謎を研究しています。
(詳しくは公式サイトをご覧ください)
この説明だと全くわからないですが、簡単にいうと後出しでポケモンを特定の単タイプに変更することができる仕組み現象です。
元と同じタイプにすることもできれば全然違うタイプにすることもでき、それぞれにメリットがあります。元と同じタイプにした場合タイプ一致倍率が1.5倍から2倍になり(つまり4/3倍)、全然違うタイプにした場合タイプ一致で放てる技の種類が増えることになります(元々のタイプの技もタイプ一致のまま)。特にポケモンSVにあるテラバーストという技を使うことでどんなテラスタルタイプであってもそのタイプと同じタイプの技を使うことができるようになるのです。
テラスタルまで考慮するとタイプの組合せの数は$(18 + {}_{18} C_2) \times 18=3078$通りになります。1vs1対面の場合の数に至っては$3078 + 3078 \times 3077 \div 2=4738581$通りになります。テラスタルってすごいですね。
テラスタル込みのタイプ相性
テラスタル込みでのタイプ相性を考えましょう。前置きが長いので興味がない方は結果だけご覧ください。
今回はランクマッチを想定して、次の四つの仮定を置きます。
- 自分のテラスタルタイプは相手にバレていない。
- 必要性が薄い場合テラスタルは使用しない。
- 使える技のタイプはテラスタルを使用しないなら自分のタイプだけ。テラスタルを使用した場合は自分のタイプとテラスタルタイプの1~3つ。
- 1ターン目のタイプ相性で勝ち負けを考える。
テラスタル込みの相性を考える上で、例として次の対面を考えてみましょう:
- カイリュー: ドラゴン+ひこう (ほのおテラスタル)
- ユキノオー: こおり+くさ (いわテラスタル)
カイリュー、ユキノオーはそれぞれどう行動するでしょうか。
- [カイリューサイド] テラスタルを切らないと四倍弱点のこおりを突かれてしまう一方、テラスタルを使用すればほのおタイプになりこおり、くさをどちらも半減できる上にほのお技で逆にユキノオーの四倍弱点をつくことができます。それゆえにテラスタルを使用した上でほのお技を選択するのが最善です。
- [ユキノオーサイド] テラスタルを切らないとひこうタイプの攻撃で弱点を突かれてしまう一方、いわテラスタルを使用することでひこうを半減にできます。そのためテラスタルを使用した上でこおり技を選択するのが最善です。
- ほのお→いわもこおり→ほのおも半減なのでタイプ相性は同程度と考えて良さそうです。複雑ですね。
次の例も考えましょう。タイプ一致テラスタルの例です:
- イーブイ: ノーマル (フェアリーテラスタル)
- ニャオハ: くさ (くさテラスタル)
イーブイ、ニャオハはどう行動するでしょうか。
- [イーブイサイド] ノーマルもフェアリーもくさとは等倍ダメージなのでテラスタルは使用する必要がなさそうです。そのためテラスタルなしでノーマル技を放つのが最も合理的に思えます。
- [ニャオハサイド] テラスタルを使用することでくさ技のダメージを4/3倍にすることができるため、テラスタル使用+くさ技を選択するのが最も合理的に思えます。
- 結果として4/3倍のダメージを与えられるニャオハが有利そうです。
最後にこの例を考えましょう。とりうる行動が一つに絞れない場合です。
- ファイアロー: ほのお+ひこう (フェアリーテラスタル)
- アマージョ: くさ (こおりテラスタル)
アマージョ、ファイアローはどう行動するでしょうか。
- [ファイアローサイド] ほのおもひこうもくさに対して抜群を取れるので、どちらを選んでも合理的です。今回はどちらかを0.5ずつの割合で選択すると想定しましょう。
- [アマージョサイド] テラスタルを使用しないとばつぐんを取られてしまいますが、こおりテラスタルを使用することで少なくともひこうは等倍にできます。さらにくさはファイアローに対して1/4の倍率ですがこおりは等倍になります。こおりテラスタルを使用してこおり技を選択するのが合理的そうです。
- この場合、ファイアロー→アマージョの倍率の期待値は$0.5\times 2+0.5\times 1=1.5$倍な一方、アマージョ→ファイアローの倍率は1倍なのでファイアローが有利そうです。
これらの例を踏まえ、今回は次のステップを踏んでタイプ相性を決定することにします:
- 相手のタイプを確認する(通常タイプのみ、テラスタルタイプはわからない)
- テラスタルを使うかどうか、および何タイプの技を使うかを両者が決定する。
- 選択した結果のダメージ倍率の大小で勝ち負けを決める
(なお2.において有効性が同じくらいの選択肢が複数ある場合、テラスタルを使用しないものを選ぶ。それでも複数ある場合は倍率の平均を使用する)
一番複雑な行動決定に関しては数式よりコードのほうがわかりやすいかと思うので以下にコードを貼ります:
def calculate_eff(src_type: int, dst_types: List[int]) -> float:
eff_sum = 0
src_table = TYPE_EFFICIENCY[src_type]
for dst_type in dst_types:
if dst_type not in src_table:
# 無効タイプには0倍を返す
return 0.0
eff_sum += src_table[dst_type]
return 2.0 ** (eff_sum)
# AがBに対してどの選択をするかを計算する
def decide_move_n_terastal(types_a: List[int], terastal_a: int, types_b: List[int]):
eps = 1e-10
# A視点でBがどの技を出すかを計算する
b_moves = [] # Bが出しうる技
r_ba = None # Bが出す技のダメージ倍率
if len(types_b) == 1:
b_moves.append(types_b[0])
r_ba = calculate_eff(types_b[0], types_a)
else:
assert len(types_b) == 2
r_ba_0 = calculate_eff(types_b[0], types_a)
r_ba_1 = calculate_eff(types_b[1], types_a)
if abs(r_ba_0 - r_ba_1) < eps:
# どちらも同じダメージ倍率なら両方を選択肢に入れる
b_moves.append(types_b[0])
b_moves.append(types_b[1])
r_ba = r_ba_0
elif r_ba_0 > r_ba_1:
b_moves.append(types_b[0])
r_ba = r_ba_0
else:
assert r_ba_1 > r_ba_0
b_moves.append(types_b[1])
r_ba = r_ba_1
# AからBへのタイプ倍率を計算する
a_move = types_a[0] # Aが出す技
r_ab = calculate_eff(types_a[0], types_b) # Aが出す技のダメージ倍率
if len(types_a) > 1:
assert len(types_a) == 2
r_ab_1 = calculate_eff(types_a[1], types_b)
if r_ab_1 > r_ab:
a_move = types_a[1]
r_ab = r_ab_1
# Aがテラスタルを使用するか決める
r_ab_terastal = max(r_ab, calculate_eff(terastal_a, types_b) * 2.0 / 1.5) # テラスタルを使用した場合のダメージ倍率
r_ba_terastal = 0.0 # テラスタルを使用した場合のBのダメージ倍率、b_movesが二つあるなら平均を取る
for b_move in b_moves:
r_ba_terastal += calculate_eff(b_move, [terastal_a])
r_ba_terastal /= len(b_moves)
# テラスタルを使用しない場合の利得を計算する
gain_wo_terastal = None
if abs(r_ab - r_ba) < eps:
gain_wo_terastal = 0 # 引き分け
elif r_ab > r_ba:
gain_wo_terastal = 1 # Aの勝利
else:
assert r_ba > r_ab
gain_wo_terastal = -1 # Bの勝利
# テラスタルを使用する場合の利得を計算する
gain_with_terastal = None
if abs(r_ab_terastal - r_ba_terastal) < eps:
gain_with_terastal = 0 # 引き分け
elif r_ab_terastal > r_ba_terastal:
gain_with_terastal = 1 # Aの勝利
else:
assert r_ba_terastal > r_ab_terastal
gain_with_terastal = -1 # Bの勝利
# テラスタルを使用するか決める
use_terastal = False
if gain_with_terastal > gain_wo_terastal:
use_terastal = True
if r_ab_terastal > r_ab:
a_move = terastal_a
return a_move, use_terastal
この行動選択の結果をもとに双方向のダメージ倍率を計算して勝ち負けを決定することにします。
結果
作成した勝ち負けポイント行列を使って混合戦略のナッシュ均衡を計算してみましょう。結果は以下の通りです。上位の複合タイプに関しては該当するポケモンも載せておきます(最終進化のみ、ポケ徹様調べ):
[順位] 通常タイプ (テラスタルタイプ): 選択確率
[1位] ノーマル (ゴースト): 0.0379
[2位] ノーマル+かくとう (ゴースト): 0.0360 (メロエッタ(ステップ))
[3位] ほのお (ドラゴン): 0.0359
[4位] ドラゴン+フェアリー (みず): 0.0298 (メガチルタリス)
[5位] ノーマル+ゴースト (かくとう): 0.0296 (ヒスイゾロアーク)
[6位] みず (フェアリー): 0.0276
[7位] みず+くさ (はがね): 0.0248 (ルンパッパ)
[8位] でんき (フェアリー): 0.0237
[9位] でんき+はがね (じめん): 0.0232 (ジバコイル、トゲデマル)
[10位] ゴースト+あく (フェアリー): 0.0221 (ヤミラミ、ミカルゲ)
[11位] いわ+あく (くさ): 0.0221 (バンギラス)
[12位] ノーマル+くさ (ほのお): 0.0212 (メブキジカ、オリーヴァ)
[13位] くさ (いわ): 0.0210
[14位] みず+ゴースト (はがね): 0.0209 (イダイトウ)
[15位] いわ (くさ): 0.0186
[16位] こおり (でんき): 0.0185
[17位] ノーマル+こおり (みず): 0.0176 (該当なし)
[18位] ひこう+ドラゴン (はがね): 0.0173 (カイリュー、チルタリス、ボーマンダ、オンバーン)
[19位] どく (じめん): 0.0170
[20位] ひこう+フェアリー (じめん): 0.0168 (ラブトロス)
[21位] ノーマル+むし (でんき): 0.0162
[22位] かくとう (はがね): 0.0161
[23位] ドラゴン (はがね): 0.0159
[24位] どく+フェアリー (みず): 0.0156
[25位] むし+ドラゴン (はがね): 0.0153
[26位] みず+はがね (くさ): 0.0150
[27位] ひこう+はがね (じめん): 0.0150
[28位] じめん+あく (どく): 0.0146
[29位] じめん (こおり): 0.0142
[30位] ほのお+はがね (ドラゴン): 0.0139
[31位] じめん (フェアリー): 0.0134
[32位] あく+はがね (ドラゴン): 0.0132
[33位] ほのお+ひこう (ドラゴン): 0.0123
[34位] どく+エスパー (あく): 0.0120
[35位] みず+でんき (ひこう): 0.0118
[36位] ドラゴン+あく (はがね): 0.0104
[37位] じめん (はがね): 0.0103
[38位] みず+じめん (ひこう): 0.0102
[39位] ゴースト (かくとう): 0.0094
[40位] ひこう+いわ (でんき): 0.0094
[41位] みず+エスパー (はがね): 0.0093
[42位] でんき+ドラゴン (フェアリー): 0.0091
[43位] どく+ドラゴン (みず): 0.0090
[44位] ノーマル+でんき (ゴースト): 0.0090
[45位] ノーマル+フェアリー (ゴースト): 0.0088
[46位] ノーマル+フェアリー (ほのお): 0.0084
[47位] こおり+いわ (みず): 0.0084
[48位] ゴースト+ドラゴン (フェアリー): 0.0081
[49位] ノーマル+ほのお (フェアリー): 0.0080
[50位] じめん+いわ (くさ): 0.0077
[51位] くさ+じめん (ほのお): 0.0077
[52位] ゴースト+ドラゴン (はがね): 0.0073
[53位] くさ+むし (はがね): 0.0070
[54位] ゴースト+はがね (ドラゴン): 0.0069
[55位] みず+あく (どく): 0.0067
[56位] あく+はがね (ひこう): 0.0066
[57位] どく+ひこう (じめん): 0.0065
[58位] ゴースト (あく): 0.0064
[59位] はがね (ドラゴン): 0.0061
[60位] いわ+ドラゴン (みず): 0.0058
[61位] ノーマル+ひこう (でんき): 0.0058
[62位] くさ+エスパー (いわ): 0.0058
[63位] ひこう+あく (はがね): 0.0058
[64位] でんき (ひこう): 0.0054
[65位] じめん+はがね (ドラゴン): 0.0054
[66位] でんき+はがね (ひこう): 0.0054
[67位] ほのお+でんき (フェアリー): 0.0053
[68位] ノーマル+あく (ゴースト): 0.0052
[69位] みず+あく (はがね): 0.0049
[70位] ほのお+フェアリー (みず): 0.0044
[71位] かくとう (こおり): 0.0041
[72位] みず+ひこう (じめん): 0.0041
[73位] くさ+でんき (いわ): 0.0039
[74位] ドラゴン (みず): 0.0038
[75位] こおり+どく (みず): 0.0036
[76位] ほのお+でんき (みず): 0.0034
[77位] みず+じめん (はがね): 0.0027
[78位] じめん+いわ (ひこう): 0.0027
[79位] かくとう+ゴースト (はがね): 0.0026
[80位] ドラゴン (ほのお): 0.0025
[81位] ノーマル+フェアリー (でんき): 0.0024
[82位] ほのお+むし (みず): 0.0021
[83位] みず+エスパー (ドラゴン): 0.0019
[84位] ひこう+フェアリー (でんき): 0.0017
[85位] あく (かくとう): 0.0017
[86位] でんき+エスパー (あく): 0.0011
[87位] あく (どく): 0.0010
[88位] ほのお+じめん (ひこう): 0.0007
[89位] かくとう+ゴースト (どく): 0.0007
[90位] ノーマル+じめん (ゴースト): 0.0006
[91位] でんき+どく (あく): 0.0006
[92位] ほのお+あく (みず): 0.0003
[93位] ドラゴン+フェアリー (はがね): 0.0001
それ以外: 0
繰り返しになりますがこの選択確率に従ってタイプを選択することで相手がどんな戦略を取ろうが勝ち負けポイントの期待値が必ず0以上になります。また、選択確率が大きいほど高頻度に出したほうがいいことになるので、選択確率は一種の強さの指数とも考えられます。
以下に軽く感想を書きます:
- 選択確率トップはノーマル(ゴーストテラスタル)でした。確かに唯一の弱点であるかくとうを無効化できるので相性は良さそうです。
- 単タイプの活躍が目立ちますね。1位、3位、6位、8位、13位...など上位にたくさんランクインしています。複合タイプじゃんけんの結果では単タイプは使わないほうがいいという結論でしたが、テラスタルありでは単タイプのポケモンも活躍しやすくなると考えられるのでテラスタルっていい
仕組み現象ですね。 - 複合タイプ界の最強はヒスイゾロアーク(ノーマル+ゴースト、かくとうテラスタル)でした。ヒスイゾロアークは弱点があくタイプしかない上に二タイプ半減、三タイプ無効化にできることで有名ですが、かくとうテラスタルを使うと唯一の弱点のあくに対して有利を取れることになるので強そうです。パルデアに来る日が楽しみです。
- 11位にあく+いわ(くさテラスタル)がランクインしています。あく+いわといえば通称600族のバンギラスが有名ですよね。
- 18位にひこう+ドラゴン(はがねテラスタル)がランクインしています。ポケモンSVのランクマッチで最強格と言われるカイリューもひこう+ドラゴンですが、はがねテラスタルカイリューはランクマ実況でもよく見ます。はがねテラスカイリューの強さがデータでも証明されてしまいました。
- タイプ一致テラスタルは残念ながらランクインしませんでした。あくまで今回のテラスタルじゃんけんにおいてはタイプ一致テラスタルは使わないほうがいいといえそうです。
- むし、どくがちらほら見られます。単タイプじゃんけん、複合タイプじゃんけんでは選択しないほうがいいという結論でしたがテラスタルのおかげで選択する価値のあるタイプになったと考えることができます。テラスタルってすごい。
(この結果がナッシュ均衡になる唯一の解だと思っていますが、詳しく調べるのに時間がかかるので他にナッシュ均衡がないとは断言しないでおきます。)
まとめ
- 【単タイプじゃんけん】 はがね、ドラゴン、みずの三タイプがTop tier。次点はゴースト、じめん、フェアリー。
- 【複数タイプじゃんけん】 一番選択したほうがいいタイプはくさ+いわ(ポケモンではユレイドル系統の固有タイプ)。ガブリアスでお馴染みのじめん+ドラゴンはこの分析でも強かった。
- 【テラスタルじゃんけん】 一番選択したほうがいいタイプはノーマル(ゴーストテラスタル)。はがねテラスタルカイリュー(ひこう+ドラゴン)はこの分析でも強かった。
- テラスタルなしの場合、最弱はむしとどく。選択しても負けやすくなるだけ。ただしテラスタルありなら全タイプに活躍の機会がある。
ここまで読んでくださりありがとうございました!よきポケモンライフを。
補足
投稿者
- ポケモンSVプレイ済。ポケモンはエメラルド以来。ユレイドルって誰?
- コンタクト: @gutta_tokyo
関連記事
- ポケモンの最強タイプを全力で考える【グラフ理論】: 違うアプローチで最強タイプの特定に挑まれていて面白いです。
min-max問題の解き方
今回取り組んだmin-max問題は以下です:
\max_{\textbf{x}\in \textrm{S}} \min_{\textbf{y}\in \textrm{S}} \textbf{x}^T A \textbf{y},
where\quad\textrm{S}=\{\textbf{x}|0\le\textbf{x}_i\le1, \sum \textbf{x}_i=1\},
一見$\textbf{x}$と$\textbf{y}$を交互に最適化していけば解けそうな気もしますがそれだと無限ループに陥ってしまうんですよね。そこで今回は上記の式を直接解くのではなく、対称ゼロサムゲームになっていることを利用して次の条件を満たす$\textbf{x}$を探すことにします:
(\textbf{x}^T A)_i \ge 0 \space for \space i \in \{1, ..., n\}
これを満たす$\textbf{x}$が本当に上記のmin-max問題の解になっているのかという話なんですが、$y_i \ge 0$であることから$\textbf{x}$がこれを満たすなら任意の$\textbf{y}$に対して$\textbf{x}^T A\textbf{y}\ge 0$になります。さらに対称ゼロサムゲームである場合$\max_{\textbf{x}\in \textrm{S}} \min_{\textbf{y}\in \textrm{S}} \textbf{x}^T A \textbf{y}$は0になることから、得られた$\textbf{x}$は上記のmin-max問題の解に必ずなっていると言えるわけです。
上記の制約を満たす$\textbf{x}$は線形計画法ソルバーを使えば解くことができます。pythonであればpulpを使うのが簡単です。今回実装した関数は以下です:
import pulp
def solve_lp(matrix, equib_value=0.0):
assert (matrix == -matrix.T).all() # Confirm this is a symmetric game.
assert matrix.sum() == 0 # Confirm this is a zero-sum game.
n = matrix.shape[0]
prob = pulp.LpProblem(name='KnapSnack')
x = [pulp.LpVariable('x_%d' % i, lowBound = 0, upBound = 1) for i in range(n)]
# prob += <ナッシュ均衡が一つに定まらないならここに最小化したい関数を追加する、必要なければなくてもよい>
prob += pulp.lpSum(x) == 1.0
for vec in matrix.T:
prob += pulp.lpSum([x[i] * val for i, val in enumerate(vec)]) >= equib_value
sol = prob.solve()
return [var.value() for var in x]
解き方説明終わり。
なおこの問題に関しては解き方を軽く調べたんですが見つかりませんでした。ゲーム理論の研究分野では極めてよくある問題設定だとは思うのでちゃんと調べたらより効率的な解法が見つかるかもしれません。
追記
2023/07/23
(対称ゼロサムゲームを含む)双行列ゲームはLemke–Howson法により解くのが一般的なようです。ご興味のある方は調べてみてください。なお対称ゼロサムゲームにおいてのLemke–Howson法は上記の解法と完全に一致します。
また、数年前に勾配降下法の亜種で解く方法も提案されていますので、勾配降下法ガチ勢の方はこちらもぜひ: The Mechanics of n-Player Differentiable Games
2024/09/02
最近同様のアプローチを用いて「エビワラーじゃんけん」についての解析も行いました。ご興味のある方はこちらもぜひ:
-
余談ですがポケモンSVの御三家ポケモンは最終進化になるとタイプが増えてそれぞれ草→草+悪,水→水+格闘, 炎→炎+ゴーストになるんですが、これって三すくみの関係が逆転するようにタイプが追加されてるんですよね(悪は格闘に弱く、格闘はゴーストに弱く、ゴーストは悪に弱い)。気づいたときよくできてんな〜って思いました。 ↩