C#で数学パズル - リングナンバーの最大公約数はどんな数でも答えが同じなのか？ #C#

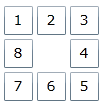
問題

下の図のようにリング状に１から８の数字が並んでいます。

1から8までの任意の数字からはじめ、右回りあるいは左回りに数字を取り出し８ケタの数字を作ります。全部で16個の数字が得られますが、この最大公約数を求めてください。

問題をどうやって解くか

結局、この問題は、
12345678 23456781 34567812 45678123 56781234 67812345 78123456 81234567 87654321 76543218 65432187 54321876 43218765 32187654 21876543 18765432

の１６個の数字の最大公約数を求める問題です。

この問題は、答えが9の倍数であることは簡単にわかるのですが、それが9の何倍なのかは、僕にはすぐにはわかりませんでした。最大公約数ということから9なのかなとは思いますが、そうでない可能性も考えられます。

ということで、プログラムでどう書くかを考えます。

Gcd(a, b, c) = Gcd(Gcd(a, b), c)

が成り立つので、以下の２つのメソッドを作成できれば、この問題を解くプログラムが作成できそうです。

8ケタの数字を求めるメソッド
２つの値の最大公約数を求めるメソッド

C#のコード

作成したプログラムは以下のようになります。

using System;
using System.Collections.Generic;
using System.Linq;

namespace RingNumberGcdApp
{
    public class RingNumberGcd {

        // ８ケタの整数から得られる16個の数の最大公約数は
        public int Solve(int baseNumber, Action<int> callBack) {
            int gcd = 0;
            int a = baseNumber;
            callBack(a);
            foreach (var b in GetNumbers(a).Skip(1)) {
                callBack(b);
                gcd = Gcd(a, b);
                a = gcd;
            }
            return gcd;
        }

        // ８桁の整数から、１６個の８ケタの整数を列挙する。
        private IEnumerable<int> GetNumbers(int num) {
            string s = num.ToString();                      // 右回り用
            string rs = new string(s.Reverse().ToArray());  // 左回り用
            return _GetNumbers(s).Concat(_GetNumbers(rs));
        }

        // GetNumbersの下請けメソッド 右回りの８つの数を列挙する
        private IEnumerable<int> _GetNumbers(string s) {
            yield return int.Parse(s);
            for (int i = 0; i < 7; i++) {
                s = RotateShift(s);
                yield return int.Parse(s);
            }
        }

        // 右へローテートシフト
        private string RotateShift(string s) {
            var s1 = new string(s.Skip(1).ToArray());
            return s1 + s[0];
        }

        // ユークリッドの互除法によるGCD 
        static int Gcd(int a, int b) {
            if (a < b)
                return Gcd(b, a);  // 引数を入替えて自分を呼び出す  
            int d = 0;
            do {
                d = a % b;
                a = b;
                b = d;
            } while (d != 0);
            return a;
        }
    }
}

using System;
using System.Linq;

namespace RingNumberGcdApp {
    class Program {
        static void Main(string[] args) {
            var dng = new RingNumberGcd();
            while (true) {
                var line = Console.ReadLine();
                if (line.Length == 8 && "12345678".All(c => line.Contains(c))) {
                    Console.WriteLine();
                    if (int.TryParse(line, out var num)) {
                        Console.WriteLine(dng.Solve(num, PrintNumber).ToString());
                    }
                } else {
                    Console.WriteLine("1-8のすべての数字を使った8桁の数値を入れてください");
                }
                //break;
            }
        }

        // 8桁の数が求められるたびに呼び出される。
        private static void PrintNumber(int n) {
            Console.WriteLine(n.ToString());
        }
    }
}

簡単なコードの解説

簡単にプログラムの説明をします。

汎用性を持たせるために、12345678 という数値以外の値も受け取れるようにしています。
Mainメソッドでは、8桁の数値を入力してもらい、RingNumberGcd.Solveに渡し最大公約数を求めています。

問題を解くRingNumberGcdクラスの主なメソッドは以下の通りです。

Solveメソッド

引数から、16個の数を生成するGetNumbersメソッドを呼び出し。
この16個の数の最大公約数を求め、結果を返しています。
なお、16個の数が正しく生成されているか知りたかったので、
生成された値を引数にコールバック関数を呼び出しています。

GetNumbersメソッド

16個の数を生成するメソッドです。
左回りの8個の数は、反転した値を_GetNumbersに渡すことで求めています。

_GetNumbersメソッド

与えられた数の右回りで得られる8個の数を求めるメソッドです。

Gcdメソッド

最大公約数を求めるメソッドです。このは、「C#:最大公約数を求める（ユークリッドの互除法）」のページで示したものと同じです。

実行結果

上記のプログラムを実行した結果です。
答えは、9であることが分かります。

実に面白いことに、65432187 8523174 82635147 13647825　など、1から8までの数字で成り立つどんな数を入れても最大公約数は9となります。（すべてを試したわけではありませんが...）

これって、紙と鉛筆だけで9であることを証明できそうな気もするのですが、
数学的知識が不足している僕にはちょと厳しそうです...

この記事は、Gushwell's C# Programming Pageで公開したものをに加筆・修正したものです。