C#で数学パズル - Triangle15パズル #C#

問題

以下のような○を組み合わせた逆三角形に「横に並んだ２つの数の差(正数)をその下の○に入れる」という条件を満たして、1～ｎまでの数字を配置します。
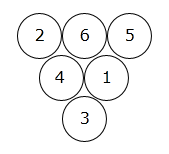
例えば、3段の三角形の場合は、以下のように 1～6までの数を入れれば、条件を満たせます。

では、5段の三角形の場合は、どのように配置すれば良いのか考えてください。

Triangle15Puzzle という名前は僕が勝手に命名したもので、本当の名前がわかりません。もしご存知の方がいれば、教えてください。

どうやって解くか

データをどのよに表現するかが問題になりますが。ここでは三角形を以下のように変形させています。

○○○○○
○○○○
○○○
○○
○

かつ、これを一次元のList<int>で表現し、C#のインデクサの機能を使い、2次元配列のようにアクセスできるようにしています。
例えば、this[0,0]は、一番左上の○を示し、this[1,3]は、2段目の一番右の○を示します。

解を求める方法ですが、まず一番上の5つの○に数字を入れます。1段目の数字が決まれば、残りの段の○は引き算をして埋めていくことができます。これで得られた15個の数字が、1～15で成り立っているかを調べています。

ようは１～15の中から5つを選ぶ順列の応用といった感じですね。
今回のプログラムでは、深さ優先の探索で再帰的処理で順列を求めて、5つを選んだらそこから三角形を作って、条件を満たしていたら正解とし、yield returnでその答えを列挙しています。

１～15の中から全て使った順列をつくり、それが条件を満たしているかを調べるという方法もありますね。ただ、この方法での実装は試していません。

C#のコード

using System;
using System.Collections.Generic;
using System.Linq;

namespace Triangle15Puzzle {
    class Solver {
        private Triangle _triangle;

        private int _steps;

        private List<int> _baseLine = new List<int>();  // 一番上の段の数字列

        public Solver(int n) {
            _steps = n;
            _triangle = new Triangle(n);
        }

        public IEnumerable<Triangle> Solve() {
            return _Solve(0, Enumerable.Range(1, _triangle.TotalCount));
        }

        private IEnumerable<Triangle> _Solve(int count, IEnumerable<int> rest) {
            if (count == _steps) {
                _triangle.BuildFrom(_baseLine);  // baeLineから三角形を作る
                if (_triangle.IsCorrect()) {     // 作成した三角形が条件を満たすか調べる
                    yield return _triangle;
                }
                yield break;
            }
            if (IsPopssible()) { // この判定は、速度アップのため （不要な探索は行わないようにする）
                foreach (var a in rest) {
                    _baseLine.Add(a);
                    var results = _Solve(count + 1, rest.Where(n => n != a));
                    foreach (var t in results)
                        yield return t;
                    _baseLine.Remove(a);
                }
            }
        }

        private bool IsPopssible() {
            // 引き算をして得られた数が、baseLineにある数と同じならばダメ。
            var q = from n in _baseLine
                    join m in Diff(_baseLine) on n equals m
                    select m;
            return !q.Any();
        }

        static IEnumerable<int> Diff(IEnumerable<int> xs) {
            var ite = xs.GetEnumerator();
            if (ite.MoveNext())
                for (int prev = ite.Current; ite.MoveNext(); prev = ite.Current) {
                    yield return ite.Current - prev;
                }
        }
    }

    class Triangle {
        private int _steps;

        private List<int> _list = new List<int>();

        public int TotalCount { get; private set; } = 0;

        public Triangle(int side) {
            _steps = side;
            TotalCount = Enumerable.Range(1, _steps).Sum();
        }

        public void Add(int n) {
            _list.Add(n);
        }

        public void Remove(int n) {
            _list.Remove(n);
        }

        public int this[int x, int y] {
            get {
                int index = Enumerable.Range(1, _steps).Reverse().Take(x).Sum() + y;
                if (index < TotalCount && index < _list.Count)
                    return _list[index];
                return 0;
            }
        }

        public int this[int index] {
            get { return _list[index]; }
        }

        public bool IsCorrect() {
            return Enumerable.Range(1, TotalCount).SequenceEqual(_list.OrderBy(n => n));
        }

        public void BuildFrom(List<int> baseLine) {
            _list = baseLine.ToList();
            int col = _steps;
            for (int i = 0; i < _steps - 1; i++) {
                for (int j = 0; j < _steps - i - 1; j++) {
                    int a = this[i, j];
                    int b = this[i, j + 1];
                    int c = Math.Abs(a - b);
                    _list.Add(c);
                }
            }
        }

        public void Print() {
            for (var i = 0; i < _steps; i++) {
                for (var j = 0; j < _steps - i; j++)
                    Console.Write("{0,3}", this[i, j]);
                Console.WriteLine();
            }
        }
    }
}

using System;

namespace Triangle15Puzzle {
    class Program {
        static void Main(string[] args) {
            int steps = 5;
            var solver = new Solver(steps);

            foreach (var tri in solver.Solve()) {
                tri.Print();
            }
        }
    }
}

コードの解説等

Solverクラスの_Solveメソッドが、実質的な解を求めているメソッドとなります。

以下のような流れで処理が進みます。

はじめは、_baseLineは空で、foreachの中で、'1'が追加されます。
再帰的に_Solveが呼び出され、その先でまた、foreachのところに行き、_baseLineに'2'が追加されます。
さらに再帰的に_Solveが呼び出され、IsPossible()がfalseになるので、この_Solveから抜け出します。
'2'の試行は終わったので、_baseLineから'2'を取り除きます。
'3'が_baseLineに追加され、_Solveが呼び出されます。 ...

4段(stps==4)の場合は、_baseLineは以下のように変化します。

1
1   2
1   3
1   3   2
1   3   4
1   3   5
1   3   5   2　　　　　--- 4つが選ばれたので、三角形を作って解かどうかを調べる
1   3   5   4　　　　　--- 4つが選ばれたので、三角形を作って解かどうかを調べる
1   3   5   6　　　　　--- 4つが選ばれたので、三角形を作って解かどうかを調べる
1   3   5   7　　　　　--- 4つが選ばれたので、三角形を作って解かどうかを調べる
1   3   5   8　　　　　--- 4つが選ばれたので、三角形を作って解かどうかを調べる
1   3   5   9　　　　　--- 4つが選ばれたので、三角形を作って解かどうかを調べる
1   3   5  10　　　　　--- 4つが選ばれたので、三角形を作って解かどうかを調べる
1   3   7   2　　　　　--- 4つが選ばれたので、三角形を作って解かどうかを調べる
... 以下省略

_baseLineに格納されている数が、_Solveを再帰的に呼び出している深さと一致します。

LINQ、IEnumerator、yield returnなどを使ってるので、これらに慣れていない方はちょっと分かりにくいかもしれませんね。

C#のコードは、任意の段(2段以上)に対応できるようにしていますが、6段以上の三角形で解を求めようとするとかなりの時間がかかります。

実行結果

２つの解が求まりました。ただし、解が鏡像なので実質的に一つですね。

でも、ちゃんと解があるってことがすごい不思議というか面白いです。

  6 14 15  3 13
  8  1 12 10
  7 11  2
  4  9
  5
 13  3 15 14  6
 10 12  1  8
  2 11  7
  9  4
  5

steps = 6 以上だと時間がかかりすぎるので、改良の余地はありますね。

この記事は、Gushwell's C# Programming Pageで公開したものをに加筆・修正したものです。