NGraphicsを使ってリサジュー曲線を描く

リサジュー曲線とは

リサジュー曲線(Lissajous curve)とは，縦方向と横方向の２つの単振動を組み合わせてできる曲線です。リサジュー図形とも言われます。

詳しくは、Wikipediaのリサジュー図形を見て下さい。
リサージュと書かれているページもあるようですが、発音的には、リサジューが近いようです。実際に聞いたことがないのでわかりませんが...

以下のような式で描く点を求めています。

x = r * sin(a*t)   0<t<2π
y = r * sin(b*t)

rは半径、aとbは任意の正数。a/bは振幅比を表します。このプログラムでは位相差は0にしています。

C#のコード

以下、NGraphicsを使ってリサジュー曲線を描くC#のコードです。IObservable<T>、IObserver<T>を実装して、描画のコードと座標を求めるコードを分離させています。

Program.cs

いわゆるメインプログラム。LissajousCurveクラス、Drawerクラスをつかって、リサジュー曲線を描いています。
aとbの値は、ここでリテラルとして記述しています。

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;

namespace LissajousCurve
{
    class Program
    {
        static void Main(string[] args)
        {
            var width = 500;
            var height = 500;
            int a = 4;
            int b = 2;
            var lc = new LissajousCurve(a, b, width, height);
            var drawer = new Drawer(width, height, $"LissajousCurve{a}_{b}.png");
            lc.Subscribe(drawer);
            lc.Start();
        }
    }
}

LissajousCurve.cs

リサジュー曲線を描くための座標を求めています。描画は、後述のDrawerクラスが受け持っています。

LissajousCurveクラスは、IObservable<T>を実装しています。購読者オブジェクト(Drawerクラス)に座標を渡して描画してもらいます。

using System;
using System.Collections.Generic;
using System.Linq;

namespace LissajousCurve
{
    // 座標
    public class Point
    {
        public float X { get; set; }
        public float Y { get; set; }
        public Point(float x, float y)
        {
            X = x;
            Y = y;
        }
    }

    // 通知データ  線分を表すクラス
    public class Line
    {
        public Point Start { get; set; }
        public Point End { get; set; }
    }

    // リサジュー曲線クラス
    public class LissajousCurve : IObservable<Line>
    {
        private int halfW;
        private int halfH;
        private int pa;
        private int pb;

        public LissajousCurve(int paramA, int paramB, int width, int height)
        {
            pa = paramA;
            pb = paramB;
            halfW = width / 2;
            halfH = height / 2;
        }

        public void Start()
        {
            int startx = (int)(halfW * Math.Sin(0));
            int starty = (int)(halfH * Math.Sin(0));
            double rad = 0.0;
            int prevx = startx;
            int prevy = starty;
            do
            {
                rad += 0.02;
                int x = (int)(halfW * Math.Sin(pa * rad));
                int y = (int)(halfH * Math.Sin(pb * rad));
                Line line = new Line
                {
                    Start = new Point(prevx, prevy),
                    End = new Point(x, y)
                };
                Publish(line);
                prevx = x;
                prevy = y;
            } while (prevx != startx || prevy != starty);
            Complete();
        }

        // 終了を通知する
        private void Complete()
        {
            foreach (var observer in _observers)
            {
                observer.OnCompleted();
            }
        }

        // 状況変化を知らせるために購読者に通知する
        private void Publish(Line state)
        {
            foreach (var observer in _observers)
            {
                observer.OnNext(state);
            }
        }

        private List<IObserver<Line>> _observers = new List<IObserver<Line>>();

        public IDisposable Subscribe(IObserver<Line> observer)
        {
            _observers.Add(observer);
            return observer as IDisposable;
        }

    }
}

Drawer.cs

LissajousCurveクラスからの通知を受け取り、EasyCanvasクラスを使って線を描きます。このクラスは描くのがリサジュー曲線かどうかは関知しません。このクラスはIObserver<Line>を実装している購読者オブジェクトです。

using System;
using System.Collections.Generic;
using System.Linq;

namespace LissajousCurve
{
    class Drawer : IObserver<Line>
    {
        private EasyCanvas _canvas;

        private string _filepath;
        private int _width;
        private int _height;
        private int margin = 20;

        public Drawer(int w, int h, string filepath)
        {
            _canvas = new EasyCanvas(w + margin*2, h + margin * 2);
            _width = w;
            _height = h;
            _filepath = filepath;
        }
        public void OnCompleted()
        {
            _canvas.Write(_filepath);
        }

        public void OnError(Exception error)
        {
            throw new NotImplementedException();
        }

        public void OnNext(Line value)
        {
            var x1 = value.Start.X + _width / 2.0f + margin;
            var y1 = value.Start.Y + _height / 2.0f + margin;
            var x2 = value.End.X + _width / 2.0f + margin;
            var y2 = value.End.Y + _height / 2.0f + margin;
            _canvas.DrawLine(x1, y1, x2, y2, 
                new NGraphics.Color("#0022FF"));
        }
    }
}

EasyCanvas.cs

NGraphicパッケージを利用して、線を描いています。結果はpngファイルにしています。

using System;
using NGraphics;

namespace LissajousCurve
{
    class EasyCanvas
    {
        private IImageCanvas canvas;

        public EasyCanvas(int width, int height)
        {
            canvas = Platforms.Current.CreateImageCanvas(new Size(width, height), scale: 2);
        }

        public void SetPixel(int x, int y, NGraphics.SolidBrush brush)
        {
            canvas.FillRectangle(x, y, 1, 1, brush);
        }

        public void Write(string path)
        {
            canvas.GetImage().SaveAsPng(path);
        }

        internal void DrawLine(float x1, float y1, float x2, float y2, Color color)
        {
            canvas.DrawLine(x1, y1, x2, y2, color);
        }
    }

}

※ C#のコードは、GitHubに公開しています。

結果

aとbの値を変えて何パターンのリサジュー曲線を描いてみました。

a = 1, b = 3 の結果

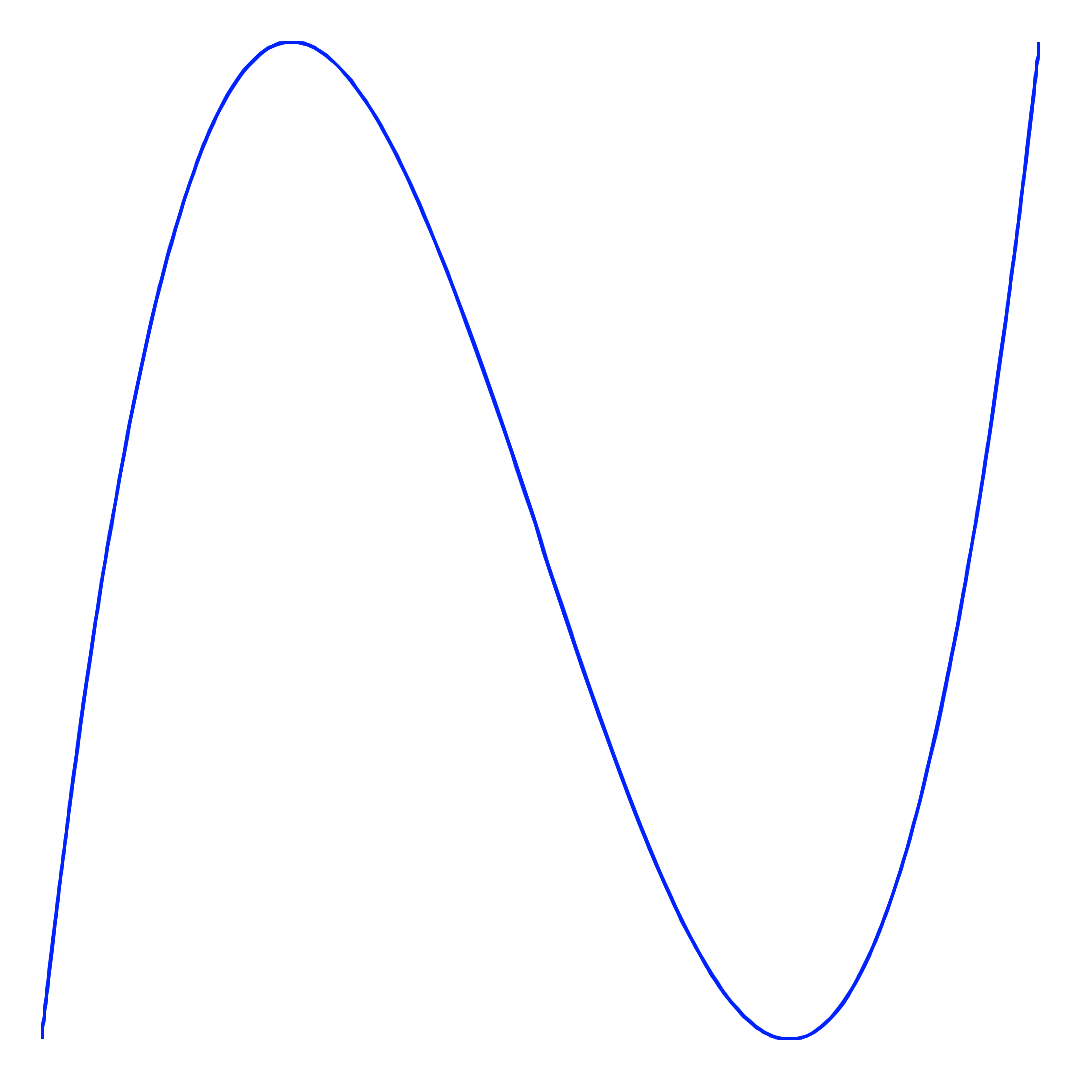
a = 1, b = 4 の結果

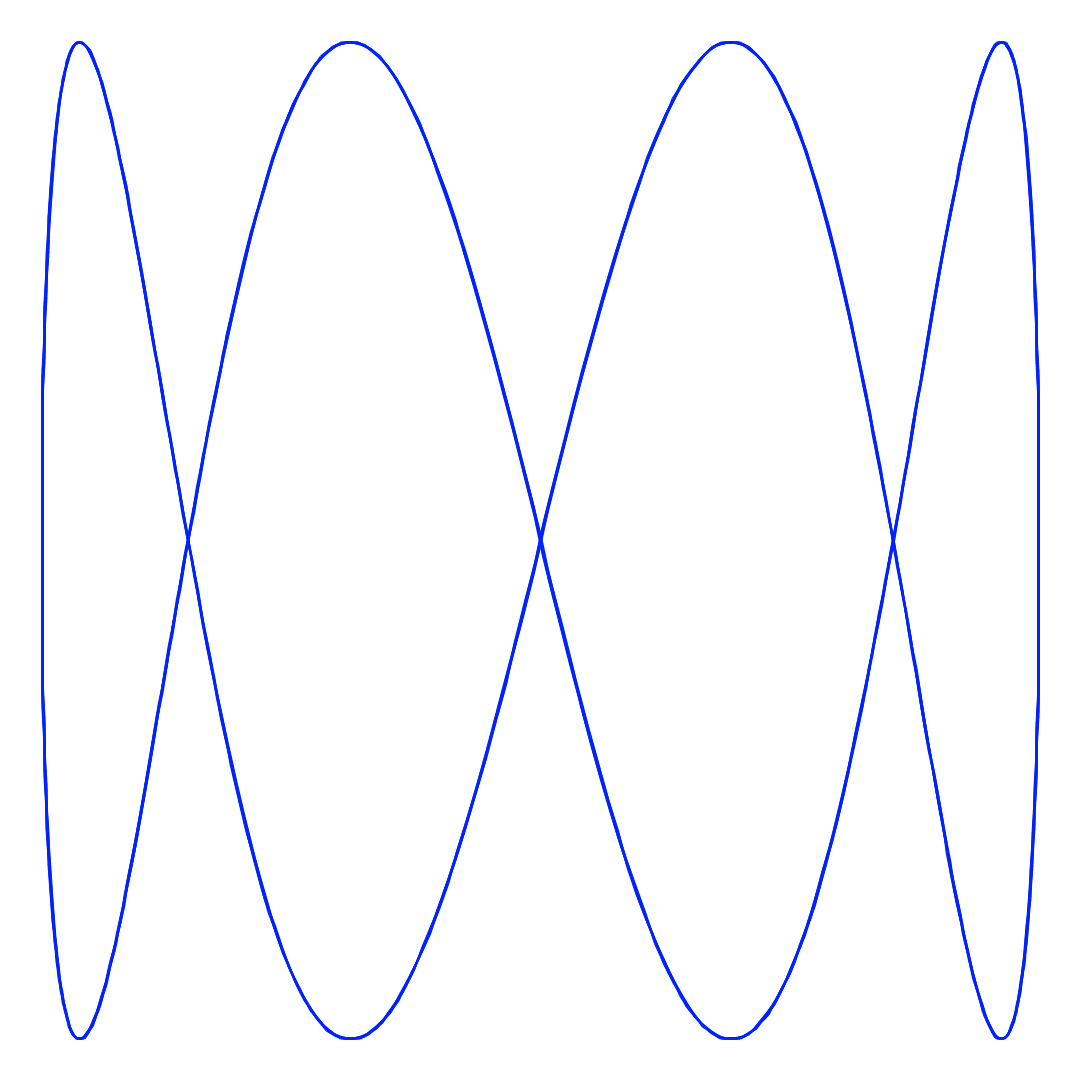
a = 3, b = 2 の結果

a = 3, b = 4 の結果

---

この記事は、Gushwell's C# Programming Pageで公開したものを加筆・修正したものです。