正n角形の完全グラフを一筆書きで描く

はじめに

正n角形の完全グラフを描くプログラムをJavaScriptで書いてみました。

頂点の数が奇数のときは、一筆書きになるようにしています。偶数のときは一筆書きはできないので、何も描いていません。

作成したプログラムの実行例

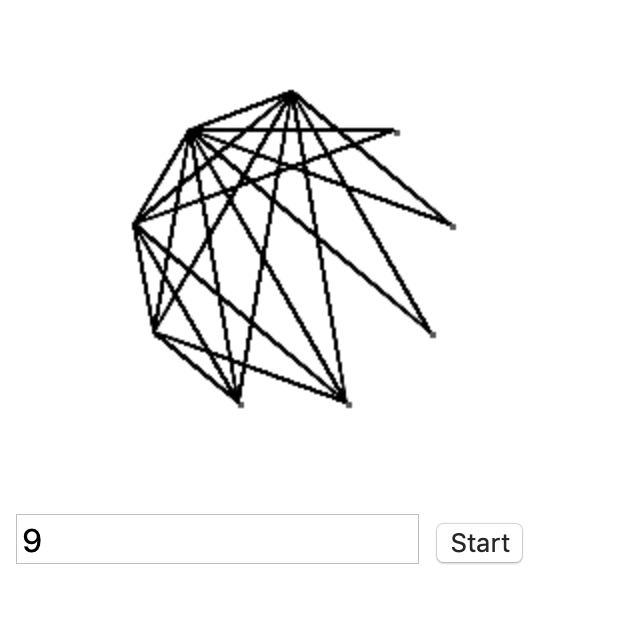
完全グラフを描いている途中のスクリーンショットです。ここでは、正9角形の完全グラフを描いています。
入力欄に整数を入れて、Startボタンを押せば、多角形の完全グラフを描くアニメーションが始まります。

次は、正9角形の完全グラフを描き終わった状態のスクリーンショット

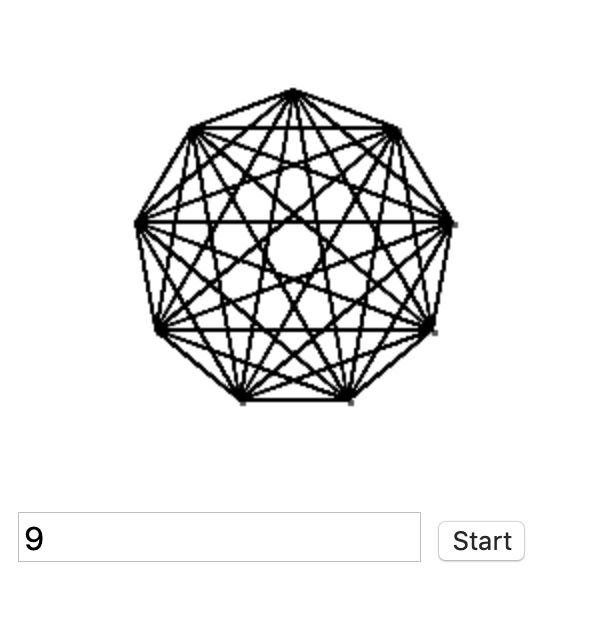
この記事の最後に、CodePenで書いたコードを貼り付けているので、実際に動きを確かめることができます。

作成したクラス

MyCanvas

CanvasAPIをラップした独自のCanvasクラス。
ここに、線を引くアニメーションのコードを実装してあります。

LineInfo

2つの頂点を結ぶ線を表すクラス。
ここで静的なフィールドを扱いたかったのだけど、JavaScriptでどう書くのが本来のやり方なのかがわからなかったです。動的型付け言語の性質を利用して宣言無しで、動的に値を代入しています。

PerfectGraph

完全グラフを表すクラス。
完全グラフに対する基本操作を実装。
ただし、完全グラフの一筆書きを求める処理はここには実装していません。

Solver

正n角形の一筆書きの完全グラフの一筆書きを求めるクラス。
再帰処理を使って求めています。

Program

実質的なMainクラス。このプログラムの制御を担当。イベント処理もここで行う。

JavaScriptのコード

MyCanvasクラス

class MyCanvas {
    constructor (id, width, height) {
        this.canvas = document.getElementById(id);
        this.ctx = this.canvas.getContext('2d');
        if (width)
            this.ctx.canvas.width = width;
        if (height)
            this.ctx.canvas.height = height;
        this.width = this.ctx.canvas.width;
        this.height =  this.ctx.canvas.height;
        // ユーザが定義するイベントハンドラ
        this.onClick = null;

        //let self = this;
        this.canvas.onclick = (e) => {
            let x = e.clientX - this.canvas.offsetLeft;
            let y = e.clientY - this.canvas.offsetTop;
            if (this.onClick)
            this.onClick(x, y);
        };
    }

    getColor(x, y) {
        let pixel  = this.ctx.getImageData(x, y, 1, 1);
        let data = pixel.data;
        return Util.toRgbaStr(data[0], data[1], data[2], data[3]);
    }

    // 線を引く
    animateDrawLine(x1, y1, x2, y2, completed) {
        var sx = x1;
        var sy = y1;
        var ex = x2;
        var ey = y2;
        var p = 0;
        let self = this;
        this.ctx.save();
        this.ctx.beginPath();
        function animate() {
            if (p < 1.00)  {
                p += 0.05;
                self.ctx.moveTo(sx, sy);
                self.ctx.lineTo(sx + (ex - sx)*p, sy + (ey - sy)*p);
                self.ctx.closePath();
                self.ctx.stroke();
                requestAnimationFrame(animate);
            } else {
                self.ctx.restore();
                completed();
            }
        }
        requestAnimationFrame(animate);
    };

    // 点を打つ
    drawPoint(x, y, color, size = 1) {
        this.ctx.save();
        this.ctx.beginPath();
        this.ctx.fillStyle = color;
        this.ctx.fillRect(x, y, size, size);
        this.ctx.restore();
    }

    // すべてをクリア
    clearAll() {
        this.ctx.clearRect(0, 0, this.width, this.height);
    }
}

LineInfoクラス

// 線の情報 from, to は頂点に振られた整数の番号を表す。
class LineInfo {
    constructor(sp, ep) {
        this.from = sp;
        this.to = ep;
    }

    // Lineの始点と終点との距離を求める（頂点番号の距離）
    getDistance() {
        let diff = Math.abs(this.from - this.to);
        return (diff > (LineInfo.NumOfApexes / 2)) ? LineInfo.NumOfApexes - diff : diff;
    }

    // NumOfApexes静的プロパティ (get)
    // 頂点の数 LineInfoのstaticメンバーとして定義
    static get NumOfApexes() {
        return LineInfo._lineinfo_numOfApexes;
    };

    // NumOfApexes静的プロパティ (set)
    static set NumOfApexes(value) {
        LineInfo._lineinfo_numOfApexes = value;
    };
}

PerfectGraphクラス

// 完全フラフに関する基本操作を担当
class PerfectGraph {
    constructor(n) {
        // linesは、すでに引いた線を記憶しておくための配列
        this.lines = [];
        // 頂点の数
        this.numOfApexes = n;
        // 処理の都合で、LineInfo.NumOfApexes にも覚えておく。
        LineInfo.NumOfApexes = n;
    }


    // 頂点の番号1..numOfApexesを順に得る
    Apexes() {
        let result = [];
        for (let i = 1; i <= this.numOfApexes; i++)
            result.push(i);
        return result;
    };

    // 頂点の数
    //getNumOfApexes() {
    //    return this.numOfApexes;
    //};

    getLines() {
        return this.lines;
    };

    // 線を引いたものとして記憶する
    addLine(line)  {
        this.lines.push(line);
    };

    // 引いた線をlinesから取り除く
    removeLine(line) {
        for (let i = this.lines.length - 1; i >= 0; i--) {
            if (this.lines[i] == line) {
                this.lines.splice(i, 1);
                break;
            }
        }
    };

    // 引数で与えた線が既に引いてある線かを調べる。 true ならば引いてある
    contains(line) {
        for (let i = this.lines.length - 1; i >= 0; i--) {
            let item = this.lines[i];
            if (item.from === line.from && item.to == line.to)
                return true;
            if (item.from === line.to && item.to == line.from)
                return true;
        }
        return false;
    };

    // 現在の頂点から引ける線の一覧を得る
    candidates(now) {
        let q = this.Apexes()
            .filter(p => p != now)
            .map(p => new LineInfo(now, p))
            .filter(line => this.contains(line) == false);
        q.sort(line => line.getDistance());
        return q;
    };

    // apexの位置から線が引けるか（空いている頂点があるか）を調べる
    canDraw(apex) {
        let q = this.Apexes()
            .filter(a => a != apex)
            .map(a => new LineInfo(a, apex));
        return !q.every(l => this.contains(l));
    };

    // 完全グラフかを調べる
    isPerfect() {
        return this.Apexes()
            .every(a => !this.canDraw(a));
    };
};

Solverクラス

// 一筆書きのパスを見つけるクラス
// 下位クラスとして、PerfectGraphクラス(完全グラフに関する基本メソッドを持つクラス)を利用。
class Solver {
    constructor(num) {
        this.pg = new PerfectGraph(num);
    }

    // 完全グラフを求める
    getPerfectGraph() {
        // 最初の頂点を引数に、_searchPathを呼び出す。
        // つまり、頂点1から始める完全グラフを求めている。
        // n角形の地点は、1,2,3,4 ..., n と1から始める。
        this._searchPath(1);
        return this.pg;
    };

    // 再帰的に完全グラフを求める
    _searchPath(now) {
        // 完全グラフならは、終了（成功）
        if (this.pg.isPerfect())
            return true;
        // 地点nowから線を引ける候補を見つける
        let candidates = this.pg.candidates(now);
        // その候補一つ一つに対して、試していく。
        for (let line of candidates) {
            // 仮に線を引く（描画はしない）
            this.pg.addLine(line);
            // 線を引いた先の地点を与えて、再帰呼び出し。
            if (this._searchPath(line.to))
                return true;
            // 失敗したので、線を削除
            this.pg.removeLine(line);
        }
        // すべての候補で試したが見つからなかった。
        return false;
    };
};

Programクラス

// Programクラス。Solverクラスを使って問題を解く。
// 描画もこのクラスで受け持つ。 ただし、実際のPixi.jsを使った描画は、MyCanvasクラスが担当。
class Program {
    constructor(width, height) {
        this.canvas = new MyCanvas('mycanvas', width, height);
    }

    run() {
        document.getElementById('solveButton')
            .addEventListener('click', () => this.solve(), false);
    };

    // 完全グラフを求める （可能ならば一筆書き）
    solve() {
        this.clear();

        let num = parseInt(document.getElementById('number').value);
        // num角形の完全グラフを求める
        let solver = new Solver(num);
        let pg = solver.getPerfectGraph();

        // ここからが描画
        let points = this.createPoints(num);
        this.drawPoints(points);

        this.drawResult(points, pg.getLines());
    }

    // 結果の描画 （完全グラフを描く 頂点の数が奇数ならば一筆書き)
    drawResult(points, lines) {
        let sequence = [];
        lines.forEach(line => {
            sequence.push({
                X1 : points[line.from - 1].X,
                Y1 : points[line.from - 1].Y,
                X2 : points[line.to - 1].X,
                Y2 : points[line.to - 1].Y
            });
        });
        this.drawLines(sequence);
    }

    // 多角形のn個の頂点を求める
    createPoints(n) {
        let points = [];
        // ここでは真上の角度を0度とする。
        let angle = 0;
        for (let i = 0; i < n; i++) {
            points.push(this.getPoint(angle));
            angle += (360 / n);
        }
        return points;
    }

    //(x-a)2+(y-b)2=r2
    //X座標 ････ 中心のx座標 + 円周の半径 * Math.cos(角度のラジアン値)
    //Y座標 ････ 中心のy座標 - 円周の半径 * Math.sin(角度のラジアン値)
    getPoint(angle) {
        // 座標を求めるのに、90度を加えてから計算
        angle += 90;
        let p = {
            X : Math.round(140 + 80 * Math.cos(2 * Math.PI * angle / 360)),
            Y : Math.round(120 - 80 * Math.sin(2 * Math.PI * angle / 360))
        };
        return p;
    }

    // すべての頂点に点を打つ
    drawPoints(points) {
        points.forEach(p => {
            this.canvas.drawPoint(p.X, p.Y, '#555555', 3);
        });
    }

    // 引数で与えられた複数の線を順番に描く
    drawLines(lines) {
        // 順番に描画する必要があるため、一つのanimateDrawLineが終わったら、次のanimateDrawLineを呼び出す。
        // animateDrawLineが非同期で実行されるので、単純なforEachだと、順番に線を引くことができない。
        let index = 0;
        let canvas = this.canvas;
        function next() {
            if (index < lines.length) {
                let line = lines[index];
                canvas.animateDrawLine(line.X1, line.Y1, line.X2, line.Y2, next);
                index++;
            }
        }
        let line = lines[index];
        this.canvas.animateDrawLine(line.X1, line.Y1, line.X2, line.Y2, next);
    }

    // 描いた線と点を消す
    clear() {
        this.canvas.clearAll();
    }
};

window.onload = function() {
    let program = new Program(250, 250);
    program.run();
};

CodePenの埋め込み

上記コードをCodePenで書いて、埋め込んでみました。

入力欄に数値を入れて、[start]ボタンを押すと描画が始まります。

See the Pen PerfectGraph by Gushwell (@gushwell) on CodePen.