[Julia] ルンゲクッタ法の実装 - Pythonとの比較 -

#前置き

　以前、 pythonで作ったルンゲクッタ法のプログラムをJuliaでも書いてみました。使い勝手はPythonと似ていますが、ブロードキャスト構文によりnumpyなどのライブラリがなくとも簡便で速い行列計算が行えることなど、コードがPythonより計算に向いているように思われます。ちなみにJuliaはVersion 1.2.0です。

#ルンゲクッタ法について
　以前にまとめましたので、下記URLを参照ください。
　https://qiita.com/guraragu0010/items/b97ea313ed1ec0cbea61

#Juliaでのルンゲ-クッタ法のプログラム

　プログラムは以下のようになりました。Pythonのものと比較していただければ、ほとんど同じように作製できていることが分かります。違うところはPythonではnumpyライブラリのzeros()を使用していましたが、Juliaではもともと実装されたzeros()を使用しています。また、Juliaのリストの添え字は0ではなく1始まりであることには注意が必要です。

#時間間隔h、時刻t、その時のyの値、標準形の右辺fを与えることで
#時刻t+1の値y+1のリストを返すルンゲクッタ法のアルゴリズム
function rk2(t,y,h)
    k1 = h*f(t,y)
    k2 = h*f(t+h/2,y+k1/2)
    y = y + k2
    return y
end


#初期時刻tini、終了時刻tlast、分割点数interval、初期条件list_yiniを与えると
#時刻のリストlist_t、ルンゲクッタ法の解のリストlist_yを返す
function rungekutta2(tini,tlast,interval,list_yini)
    #時間間隔hの計算
    h = (tlast-tini)/interval
    #初期条件の大きさの確認
    size = length(list_yini)
    
    #list_t, list_yの入れ物を作製
    list_t = zeros(interval+1)
    list_y = zeros(interval+1,size)
    
    #初期条件の格納
    list_t[1] = tini
    list_y[1,1:size] = list_yini
    
     #ルンゲクッタ法で随時計算し結果をlist_t, list_yに格納
    for i in 2:interval+1
        list_y[i,1:size] = rk2(list_t[i-1],list_y[i-1,1:size],h)
        list_t[i] = list_t[i-1]+h
    end
    return list_t,list_y
end

#ルンゲ-クッタ法のプログラムのテスト
こちらも以前と同様に、調和振動子の運動方程式を使って確認します。調和振動子の運動方程式を標準形を用いてプログラムに落とし込むと、以下のようになりました。ここでのJuliaの特徴は”pi”や”π”という文字列が円周率を表してくれることと、積の演算子”*”を省くことも可能であるということでしょうか。そのために、より数式に近いコードを書くこともできそうです。

km = 4pi^2

function f(t,y)
    freturn = [y[2], -km*y[1]]
end

　さて、時刻は0~1、分割点数を100、初期位置を0、初速を1として計算を実行してみます。

list_t1,list_y1 = rungekutta2(0,1,100,[0,1]);

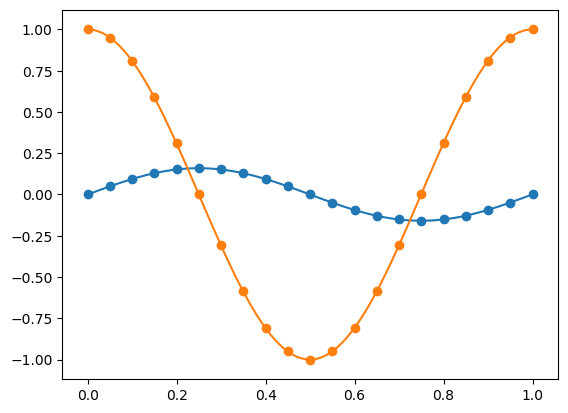
　結果を図としてプロットすると、以下のような図が出力されました。オレンジ色が速度、青色が位置を表しています。また、線が計算によるもので、ドットは理論的な解をプロットしたものです。計算結果と理論的な解がよく一致していることが分かります。また、実際に結果を比較しても1E-3程度まで一致していることが分かりました。Pythonでの出力と同程度の精度です。

まとめ

　Pythonで作製したルンゲクッタ法のプログラムをJuliaで書き直してみました。使い勝手は似ていますがJuliaの方が計算に向いた作りであるように思いました。何か間違いがあるようでしたらお教えいただければ幸いです。