前置き
タンパク質の構造のシミュレーション等に用いられる自己回避ランダムウォークのプログラムをpythonで作製したので紹介いたします。根本的な手直しができそうな気はしますが、楽しかったです。
ランダムウォークとは
ランダムウォークとは次に移動する点が無作為に選ばれる運動のことで、ランダムウォークを基礎としたモデルが様々な研究に使用されています。例えばアインシュタインが研究したことで有名なブラウン運動は水面に浮く花粉中の微粒子の不規則な動きのことですが、これもランダムウォークを使用したモデルでシミュレーションできる運動の一つです。
今回のトピックである自己回避ランダムウォークとは、自分自身の通った経路を再び通らないようなランダムウォークのことです。例えば2次元長方形格子の格子点をランダムに一筆書きで移動する運動を記述します。実際の応用としては、自己回避ランダムウォークはタンパク質の構造をシミュレーションするために用いられることがあるそうです。
自己回避ランダムウォークのプログラムを作ってみた
自己回避ランダムウォークのプログラムは、上記の性質から、①一度通った経路を避ける必要がある、②現在の位置から次に移動できる点がない(自分自身の経路によって囲まれる)とランダムウォークのシミュレーションが終わる必要があります。また、③設定した領域の境界に到達してもシミュレーションが終わるようにしました。
2次元長方形格子上での自己回避ランダムウォークのプログラムは以下のようになりました。自己回避ランダムウォークの結果を返すself_avoidance_random_walk関数の中で、現在点の周囲の点が通過済みかどうかを判定するsurrounding_points_checkerと、次の移動点の候補が既に通過済みでないかを判別し問題なければ移動を決定するnext_point_decisionerが働いているような構造となっています。(今回は移動点をリストに随時格納しているため少し回りくどくなっている気がします。マップ的なものを作製してその上を動き回る駒と移動位置を記録する部分に分けてもいいかも)
import numpy as np
import random
random.seed(None)
'''
二次元格子の最大値xmax,ymaxを与えることで
自己回避型ランダムウォークの結果を返す関数
'''
def self_avoidance_random_walk(xmax,ymax):
#初期状態の作製。
list_x = np.array([0])
list_y = np.array([0])
#random_walkのループ
roop_num = 0
while True:
#現在地の周囲の状況を確認し、通過済みの点(duplicate_num)を数える
duplicate_num = surrounding_points_checker(roop_num,list_x,list_y)
#移動できる点がなければループを抜ける
if duplicate_num >= 4:
break
#次の移動地点の候補(x_dum, y_dum)を作製
else:
D1 = random.randint(0,1)
D2 = random.randint(0,1)
dx_dum = (-1)**D1*D2
dy_dum = (-1)**D1*(1-D2)
x_dum = list_x[roop_num] + dx_dum
y_dum = list_y[roop_num] + dy_dum
#境界に達したらループを抜ける
if (abs(x_dum)==xmax or abs(y_dum)==ymax):
list_x = np.append(list_x,x_dum)
list_y = np.append(list_y,y_dum)
break
#新しい点を加える
roop_num,list_x,list_y = next_point_decisioner(roop_num,list_x,list_y,list_mono,x_dum,y_dum)
return list_x, list_y
def surrounding_points_checker(i,list_x,list_y):
#現在位置をx_cur,y_curに格納
x_cur = list_x[i]
y_cur = list_y[i]
#現在位置の周囲の位置をx_plus,y_plus,x_minus,y_minusとして表示
x_plus = x_cur+1
x_minus = x_cur-1
y_plus = y_cur+1
y_minus = y_cur-1
#周囲の既に通過した位置を記録し返す
duplicate_num = 0
for j in range(len(list_x)):
if (x_plus == list_x[j] and y_cur == list_y[j]) or (x_minus == list_x[j] and y_cur == list_y[j]):
duplicate_num +=1
elif (x_cur == list_x[j] and y_plus == list_y[j]) or (x_cur == list_x[j] and y_minus == list_y[j]):
duplicate_num +=1
else:
duplicate_num +=0
return duplicate_num
def next_point_decisioner(i,list_x,list_y,list_mono,x_dum,y_dum):
#移動地点の候補(x_dum, y_dum)が既に通過済みの地点でないか判別
k = 0
for j in range(len(list_x)):
if (x_dum == list_x[j] and y_dum == list_y[j]):
k +=1
else:
k +=0
#未通過の場合はリストに加え、通過済みの場合は候補を却下する
if k == 0:
list_x = np.append(list_x,x_dum)
list_y = np.append(list_y,y_dum)
i+=1
return i,list_x,list_y
if k == 1:
return i,list_x,list_y
自己回避ランダムウォークのプログラムの実行例
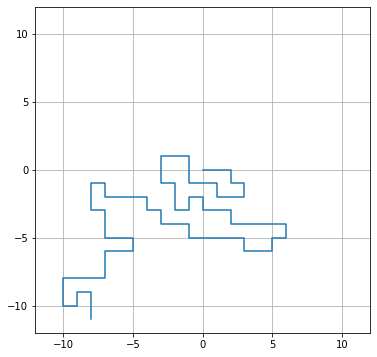
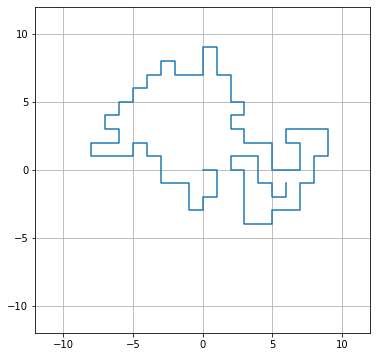
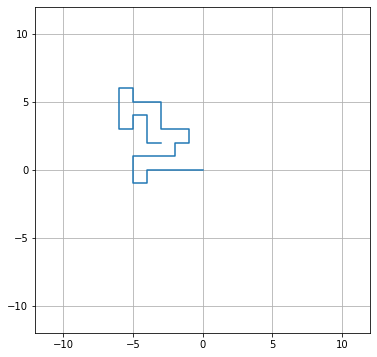
自己回避ランダムウォークのプログラムは例えば以下のように実行します。ここでは2次元長方形格子の$x$軸を$-11 \le x \le 11$、$y$軸を$-11 \le y \le 11$としています。
import matplotlib.pyplot as plt
x_max = 11
y_max = 11
list_x, list_y = self_avoidance_random_walk(x_max, y_max)
plt.figure(figsize=(6, 6))
plt.plot(list_x, list_y)
plt.grid(True)
plt.xlim(-x_max-1,x_max+1)
plt.ylim(-y_max-1,y_max+1)
plt.show()
すると、以下のようなグラフを得ることができます。中心地点から開始し末端にくるか自分自身に囲まれたときにシミュレーションが終わっていることが分かります。また、実行のたびに結果がランダムに変わります。
まとめ
今回は自己回避ランダムウォークのプログラムを作製しました。これを応用して格子点の位置にあるものの種類を指定し、構造のエネルギーの安定性などをシミュレーションすることもできます。また、もっと効率的なプログラムの方法がありそうなので今後の課題としたいと思います。
[参考書籍・ウェブ]
R.H.Landau・他 (2018)『実践Pythonライブラリー 計算物理学I -数値計算の基礎/HPC/フーリエウェーブレット解析』 (小柳義夫・他訳) 朝倉書店