ベジェ曲線同士の交点
3次ベジェ曲線同士の交点は最大で9点存在するがストレートには解けないため、
何かしらの方法で近似していく必要がある。(ちなみに片方が直線の場合は式で解ける)
今回Bezier Clipping法を用いて実装した際の仕組みと手順をメモしておく。
Bezier Clipping法とは
Bezier ClippingはBezier曲線の性質を利用することで、交点計算を安定して求める方法
Bezier曲線を分割する処理を再帰的に行うことからBezier Clipping 法と名ずけられた。当初は曲面のレイトレーシング法が目的でしたが、多項式の解法から3D物体のレンダリング(表示)まで種々の図形処理への応用が可能となった。
実際の実装にあたっては こちらの論文を参照した。
もっと簡単な方法
ベジェ曲線を含む矩形同士が被っているか判定して、被っていたら2分割していくだけの手法もある。
十分に面積が小さくなった時点で分割をやめる。そこまで遅くもなさそう。
下記の凸包性とド・カステリョが分かれば組める。
予備知識
1. ベジェの凸包性 (convex hull property)
ベジェ曲線は制御点によって作られる凸包に必ず内包される。
上のような矩形ベースでの判定は線がちょっとはみ出したりしそうな気になるけどその心配はない。
言われれば当たり前な気もするが、Bezier Clippingにおいても重要な性質となる。

2. ド・カステリョのアルゴリズム (De Casteljau's algorithm)
ベジェを任意の点で分割するときに用いる。 https://en.wikipedia.org/wiki/De_Casteljau%27s_algorithm
難しそうな名前だけれど、単にベジェ曲線を描く過程の補助線や制御点が、
そのまま分割時のハンドルやアンカーポイントとして使えてすごい、みたいな理解をしている。すごい。
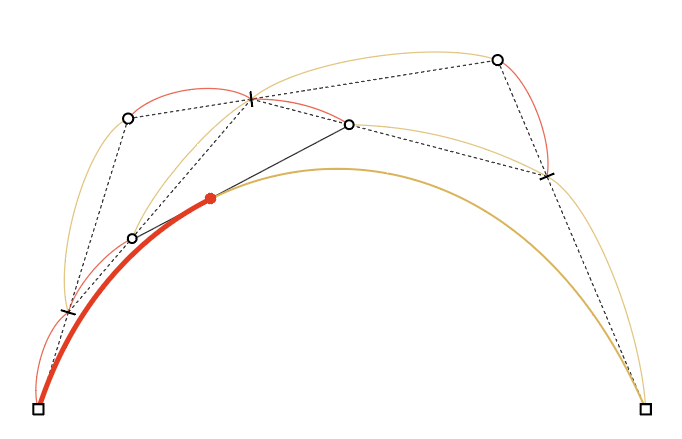
使用時に注意すべきはt=0.5で分割したからといって長さが半分になるわけではないという点。
Bezier Clipping
上にも書いたこの論文に沿って進める
大まかな流れ
対象の片方の線を太らせて、そこにもう片方の含まれる部分だけ切り出す。
それを交互に行うことで、互いの範囲を絞っていく。
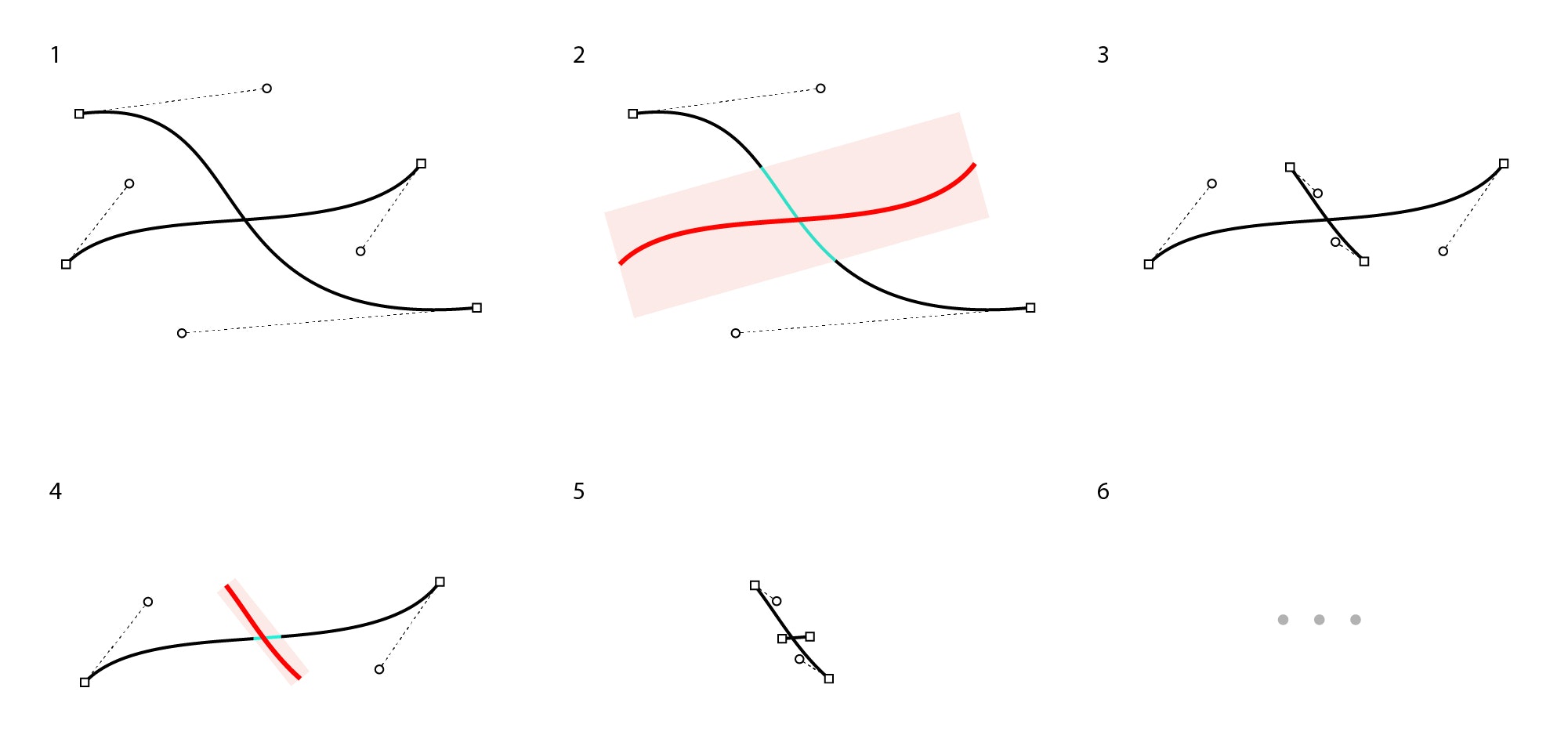
まずは下の曲線Aと曲線Bについて、切り取り1回分の操作を考えてみる。
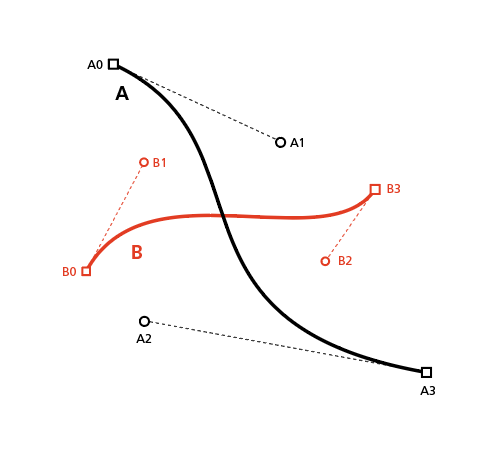
1. 曲線BのFat Lineを作る
まずは1回目の切る側(A)、切られる側(B)を決めて、切る側を太らせる。(FatLineと呼ばれる)
この「太った範囲」をどのように作るかを考えていく。
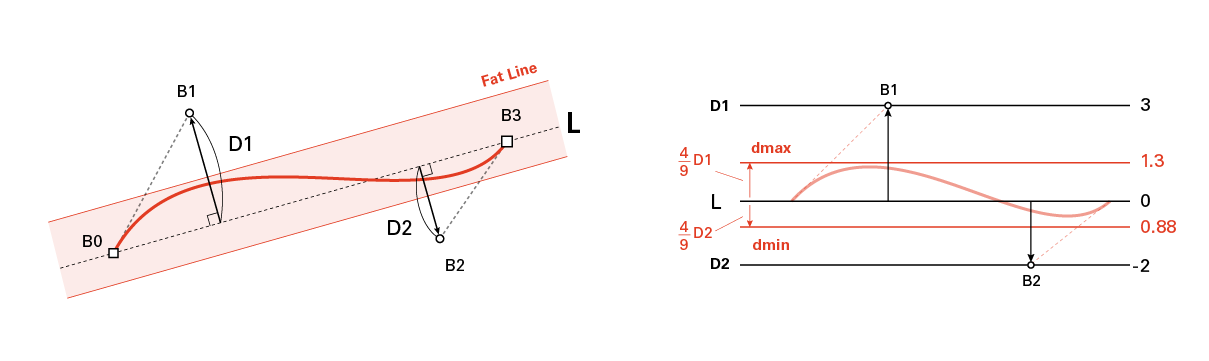
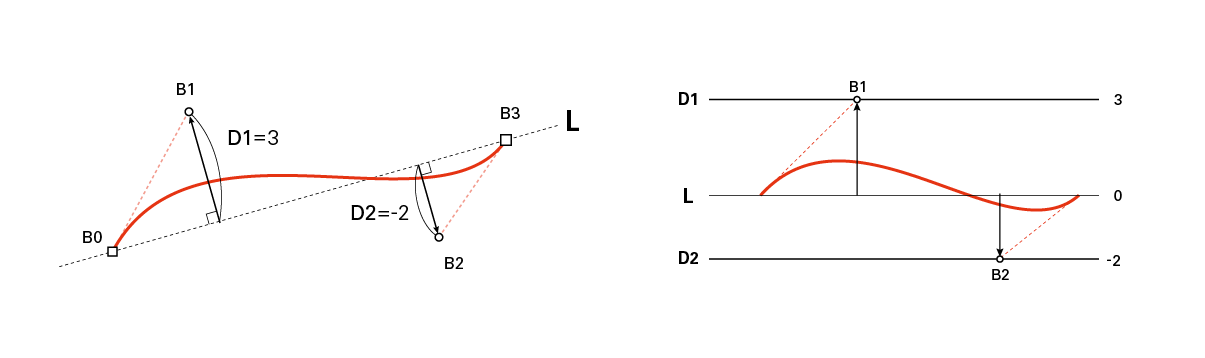
まず太らせる方のベジェの制御点B1, B2について、直線L(B0→B3)への符号付きの距離をそれぞれ求める(D1, D2)。
(参考: 直線と点の距離 分子の絶対値をとらずそのまま使う)
ベジェの凸包性から、D1〜D2幅に曲線が収まることは分かるが、このままだと無駄が多い。
正確に曲線の頭頂部までの距離を求めてギリギリの幅を出すことは一応できるが、
計算コストに見合わないため、ここでは距離符号の組み合わせ(D1, D2)から
ベジェの大まかな形状を判定した上で、距離を定数倍して狭めることにする。
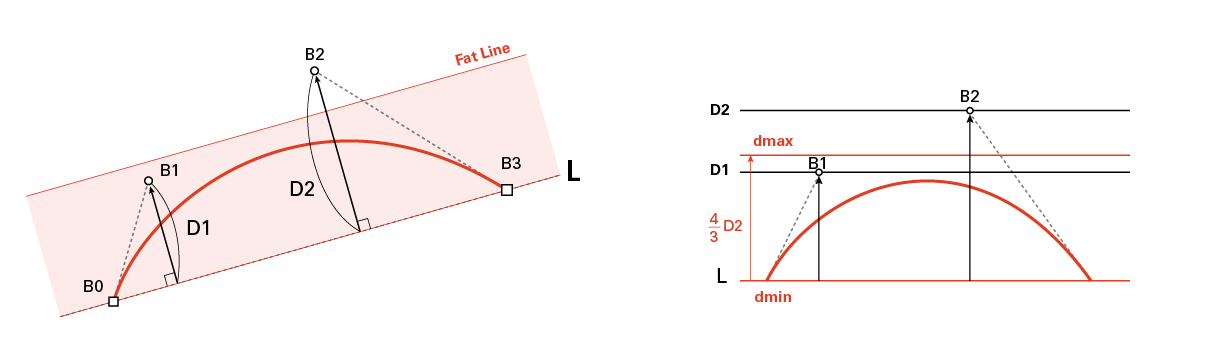
S時の場合は双方に4/9倍、円弧状の場合は最大値に3/4倍することで最大幅(dmin, dmax)とする。
(数字の根拠は理解及ばずなので元論文を参照)
どちらを使うかは**距離符号の一致/不一致(XOR)**で判定する。
2. 曲線AのFat Lineとの交差範囲を求める
今度はB0→B3の線に対してAの各制御点からの距離を求め、
ベジェのパラメータ(t)と距離(d)のグラフを作る。
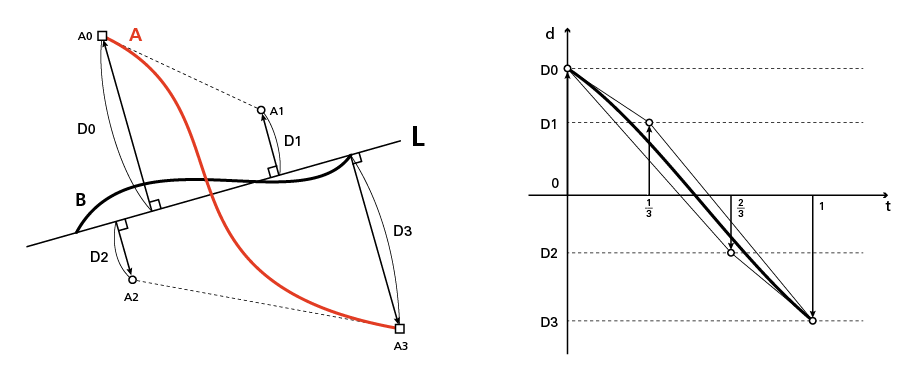
各点からの距離のグラフもまたベジェ曲線となり、凸包性が使える。
この凸包形状をそのまま用いて、先に求めたFat Lineのdmin, dmaxと組み合わせ、
tの交差している範囲tmin, tmaxを求める。
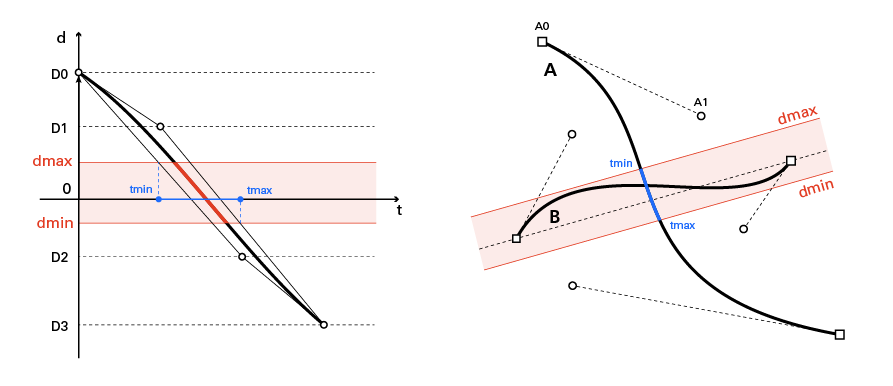
3. 曲線Aを被った範囲で切り取る
ド・カステリョを2回使ってtmin/tmaxの範囲で曲線Aの部分曲線を求める。
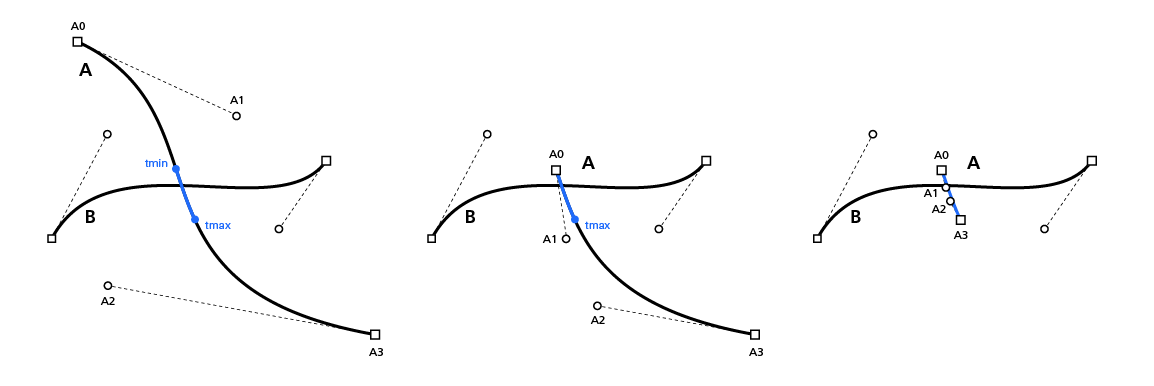
4. AとBを入れ替える
双方が十分に短くなるまでこれを繰り返す。
ケース別ハンドリング
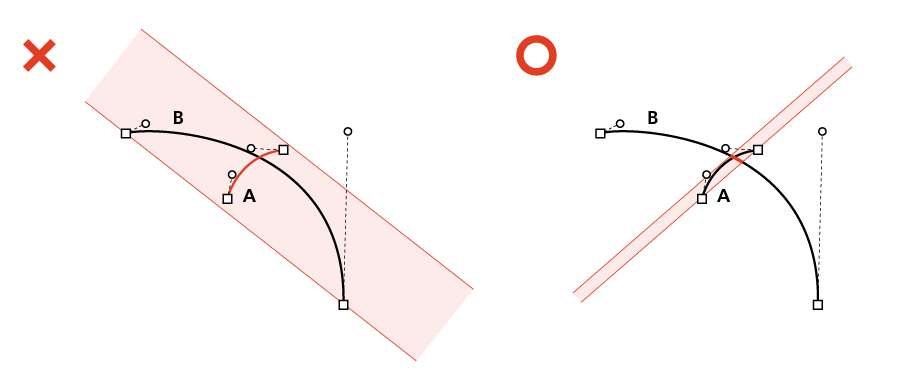
AがBのFat Lineに全て含まれる場合
この場合、Aが全て切り取られてしまうのでそこで終了してしまう。
一方で、AとBを入れ替えればかなり効率よく切り取ることができる。
特に初回は入れ替えた場合と合わせて算出しておき、
より切り取られる量(1-(tmax-tmin))の大きい方を採用するのが吉とのこと。
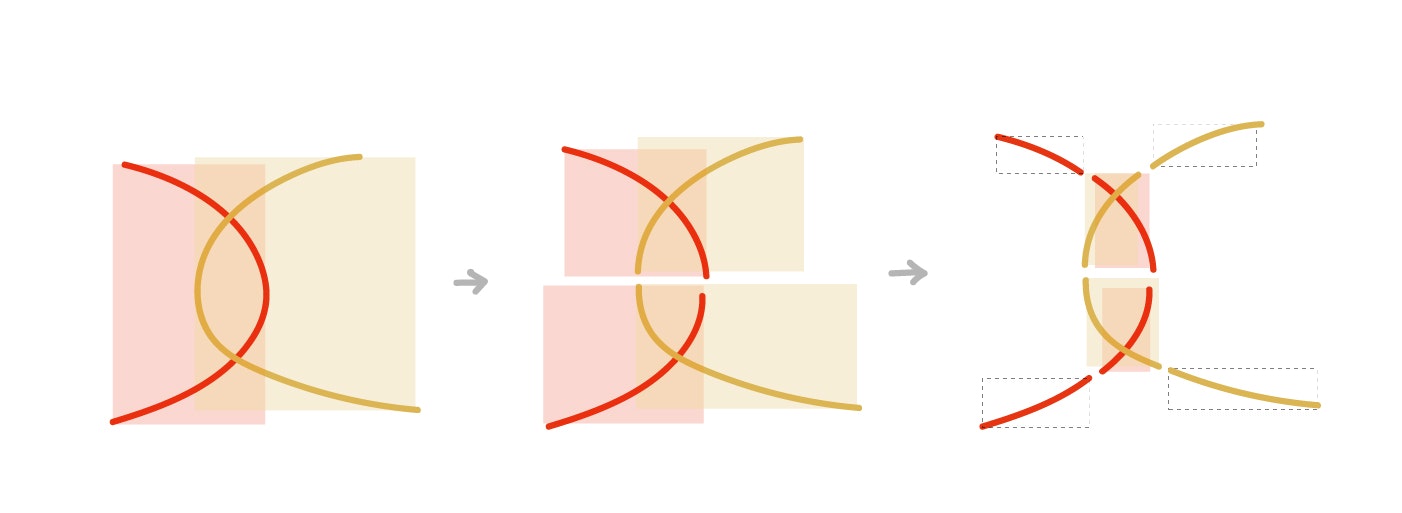
複数点での交差
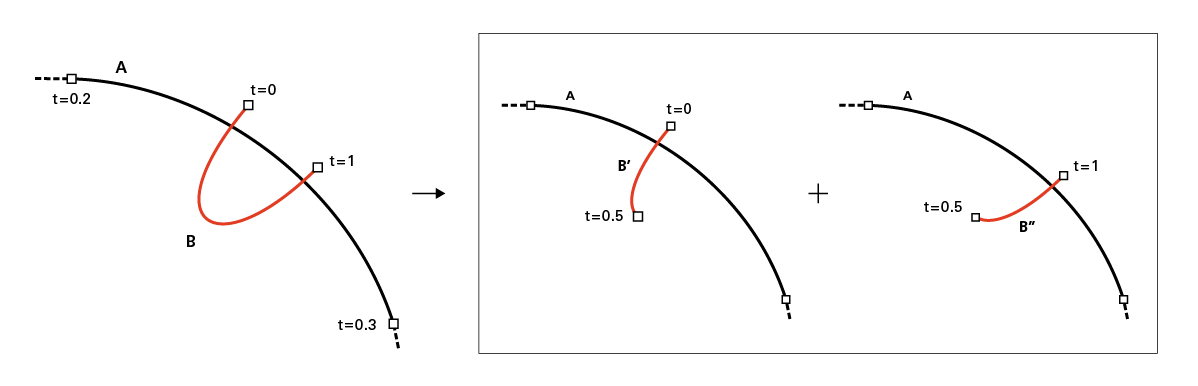
ストレートに進んだ場合、この手法では1点にしか対応できないため、
複数点で交差している場合はどこかで曲線を分割して元の曲線を増やすしかない。
判別方法としては、AとBどちらで切っても減るtの割合が20%以下の場合は、
(範囲が被っている割合が大きいということなので) 長い方※を再分割して
AB′,AB″の新たな組み合わせとしてそれぞれ処理するようにする。
この判定は初回だけでなく、その後も再帰的に行う必要がある。
※長さは実際の長さではなく、元の曲線に対して残っているベジェのパラメータ(t)
補足:様々な距離パターンの考慮
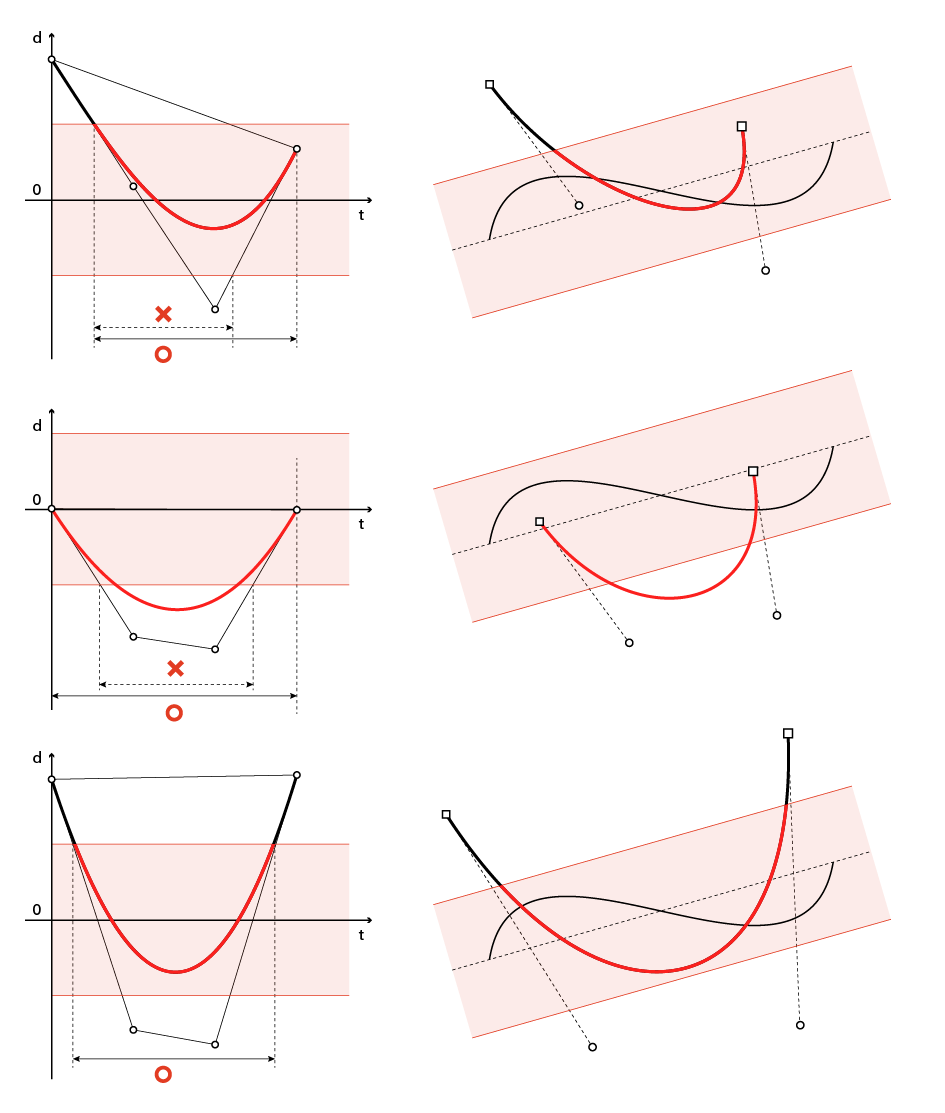
工程「2」で距離グラフの凸包とdmin/dmaxを組み合わせてtの範囲を出しているが、
「X」形のように必ずしも片方がもう片方を綺麗にまたぐ形ばかりではないため、
凸包の各辺とdmin,dmaxとの交点のみを求めても上手くいかないケースがあるので注意する。
結論としては凸包の4辺とy=dmin, y=dmaxの2直線の交点を全て出し、
そこに頂点のうちd値がdmin<=d<=dmaxであるものを加え、
最後にそれら全てのx座標のmin,maxを求めればtmin,tmaxとなる。
別の関数等で凸包x凸包の交差エリアがスムーズに出せれば、それでも良いと思う。
(初歩的すぎて論文内には特に詳しく書かれておらず少しハマったので補足)
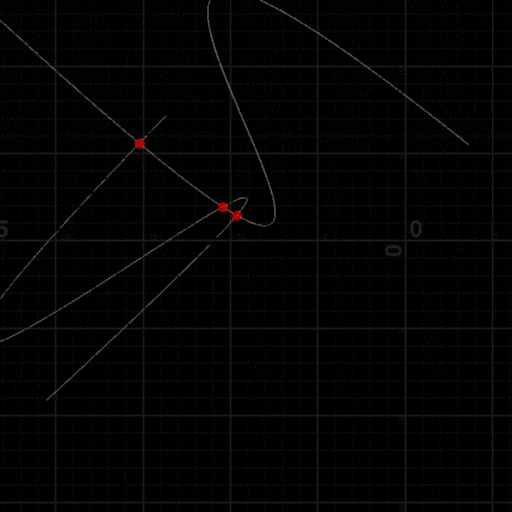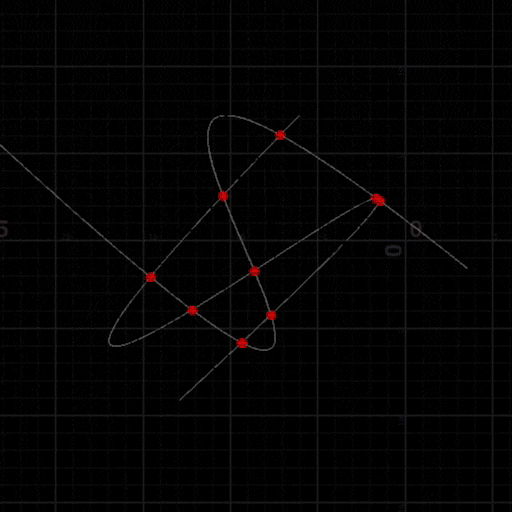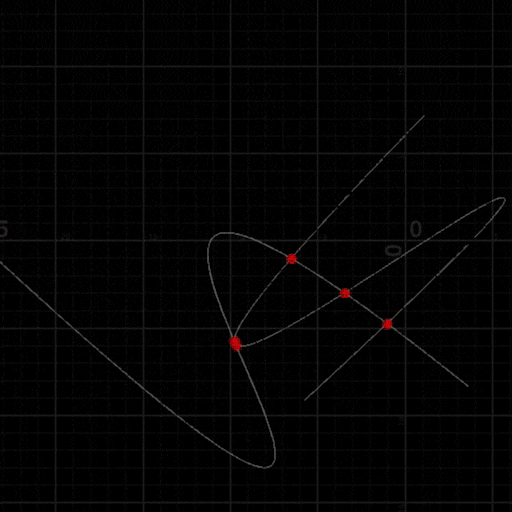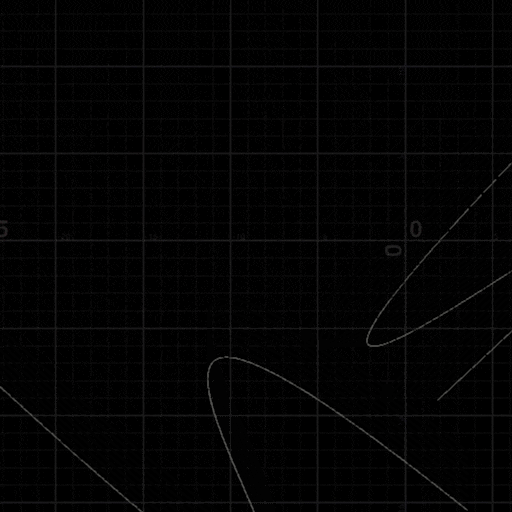
動作サンプル
HoudiniのVEXにて実装
徐々に分割・収束して最終的に全て点になる様子

交点数が変化していく様子