Haskellの気持ち #数学

はじめに

この記事は富士通クラウドテクノロジーズ Advent Calendar 2020 の17日目の記事です。
16日目は @yt09191971 さんのニフクラSDK使うには、Jupyter Notebookが以外に便利な件についてでした。
私もJupyter Notebookはデータ分析でよく使われるイメージでしたが、簡単なコードをまとめたり動かしたりするのが楽なので、様々なことに応用が利きそうですね。

改めましてこんにちは。FJCT2年目社員の @gunkan8mmt です。FJCT入社という形でクラウド業界に参入し、業務の傍らで様々な技術や概念を学んでいます。
今回の記事は、普段社内で数学の話ばかりしている私がつい最近Haskellと出会い、主観的になんとなく数学っぽいなと感じたところについてのお話になります。数学といえば堅苦しく敬遠されがちなイメージですが、考え方に慣れればこの上なく自由な学問であると私は思います。コンピュータも数学の一分野、計算機科学の賜物ですよね。

【本題】Haskellと数学の類似点

Haskellと言えば純粋関数型言語を思い浮かべる人も多いと思います。私自身、関数型言語というものが何者なのか知りたいと思い、Haskellを始めました。まだ始めたばかりではありますが、既に随所で数学と似ていると思われる点が見つかり、考え方にとても馴染みやすいと感じています。
そこで、個人的な主観をもとに、Haskellと数学の類似点についてお話ししたいと思います。なお、経験の浅い私が認識しているもののみなので、これらがすべてではありませんし、またHaskellに限った話ではないかもしれません。

letとwhere

変数の定義の時に let や where を使います。例えば次のようなものがあります。

area r = pi * square r
    where                   -- whereで局所的な変数と補助関数を定義 
        pi = 3.14
        square x = x * x

main = do
    let r = 5.0             -- letで局所的な変数を定義
    print (area r)          -- 78.5 と出力される

日本語に翻訳すればこんな感じでしょうか。

半径 $r$ の円の面積 $A(r)$ は次式で与えられる。
$A(r) = \pi \times sq(r)$
ここで $\pi=3.14$ 、 $sq(r)=r^2$ である。
今、円の半径を $r=5.0$ とすると、その円の面積は
$A(r) = 78.5$
である。

Haskellの構文とかなり近いと思いませんか？意図的に寄せた部分もありますが、それでも自然な形で表現できていると思います。

また、 let や where は、英語の記事や論文などでもほぼ同じ用途で使われることが多いです。例えばwikipediaのオイラーのφ関数（英語版）の記事で let と where を検索すると実際の使い方がわかります¹。日本語版の記事も、英語版の記事に完全に対応しているわけではありませんが、「ここで○○は～」という表現が使われていますね。
論文中で let と where のどちらを使うかについての決まりはないと思いますが、なんとなく let は式の評価の前に使い、「この変数の値をこれとして式を計算しますよ」と宣言するようなイメージがあります。一方で、 where は式の定義の直後で使い、「式中のこの変数/関数はこういう意味です」と説明していることが多い気がします。

関数の型宣言

Haskellでは、関数の型宣言は必須ではありませんが、書いておくとわかりやすいです。
たとえば Int 型の引数を一つとり、 Float 型の値を返す関数 $f$ の型宣言は次のように書けます。

f :: Int -> Float

一方数学では、整数の引数を一つとり、実数を返す関数 $f$ は次のように表現されます。

f : \mathbb{Z} \rightarrow \mathbb{R}

見た目がほぼ同じであることがわかると思います。Haskellは数学だと言われる理由が、このような細かいところからも読み取れるような気がします。

さて、数学のこの書式ですが、より一般に集合 $X$ （定義域）の要素が関数 $f$ によって集合 $Y$ （値域）に写る場合は次のように書きます。

f : X \rightarrow Y

この時のイメージは関数 $f$ によって集合 $X$ の要素 $x$ がそれぞれ集合 $Y$ の対応する要素 $f(x)$ に変換されるというものになります。数学でいうところの「集合 $X, Y$」「 $x$ 」「 $f(x)$ 」がそれぞれちょうどHaskellの「型」「引数」「返り値」に対応しています。

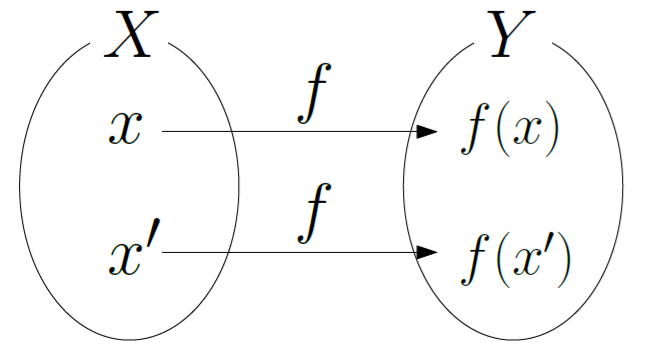
Haskellでは数値だけでなく、文字列なども対象になることがあります。もちろん数学でも数値以外を扱うことはできるのですが、数値以外のより一般のものを変換する時は「写像」という言葉を使います²。言い換えれば、関数は数値を扱うタイプの写像です。

もう少し写像についてお話しすると、先ほどのイメージ図からもわかるように、定義域の要素は写像 $f$ によって値域の要素に写ります。写像の性質として、定義域の値が一つ決まると、それに対応する値域の値も常に同じ一つの値に定まります（被る場合もあります）。数学、特に集合論ではこのような性質を写像に持たせるため、写像を定義域の要素と値域の要素の組で定義することがあります。例えば $f(x)=x^2$ という写像 $f$ は $(-1,1), (2,4), (1.5,2.25), \cdots $ といった組を持つ集合として定義されます³。
これを考えれば、シード値のない乱数を関数として定義できないのも、また関数は参照透過性を持つという性質も、数学の関数（写像）を模しているのであれば当然の性質とも言えますね。

関数の合成

最後に関数の合成についてお話しします。

Haskellでは関数同士を結合し、合成関数を作ることができます。
どこで役立つかはわかりませんが、整数のリストを受け取って2乗和を計算し、その結果が5の倍数であるかを判定する関数 isMultipleOfFiveSum を作成してみましょう。

sqSum :: [Int] -> Int                           -- 2乗和を計算する関数
sqSum [] = 0
sqSum (x:xs) = x^2 + sqSum xs

isMultipleOfFive :: Int -> Bool                 -- 5の倍数の判定をする関数
isMultipleOfFive n
    | n `mod` 5 == 0 = True
    | otherwise = False

isMultipleOfFiveSum :: [Int] -> Bool            -- 2乗和が5の倍数か判定する関数
isMultipleOfFiveSum = isMultipleOfFive . sqSum  -- 関数の合成

isMultipleOfFiveSum の定義のところで関数の合成を行いました。あとは isMultipleOfFiveSum [1..10] のように使えば、2乗和が5の倍数であることの判定ができます。

他の言語でも関数の合成に近いことはできるのですが、括弧が必要になったりするので見た目がわかりにくくなることがあります。その点Haskellでは括弧を使わず、演算子 . で合成できるので見やすくて良いですね。一度合成してしまえば、引数と返り値の型は一連の合成関数の最初と最後だけ見れば良いというのも単純で分かりやすいと思います。

これは数学の「合成関数」を模しています。 $f \circ g$ というものです。 $f(g(x))=(f \circ g) (x)$ なので、意味としては「『 $x$ を $g$ で写したもの』を $f$ で写したもの」というものになります。
isMultipleOfFiveSum の例では Int 型のリスト（ [Int] ）を受け取り Int 型に変換した後、さらにそれを Bool 型にするということですね。イメージにすると下図のようになります。

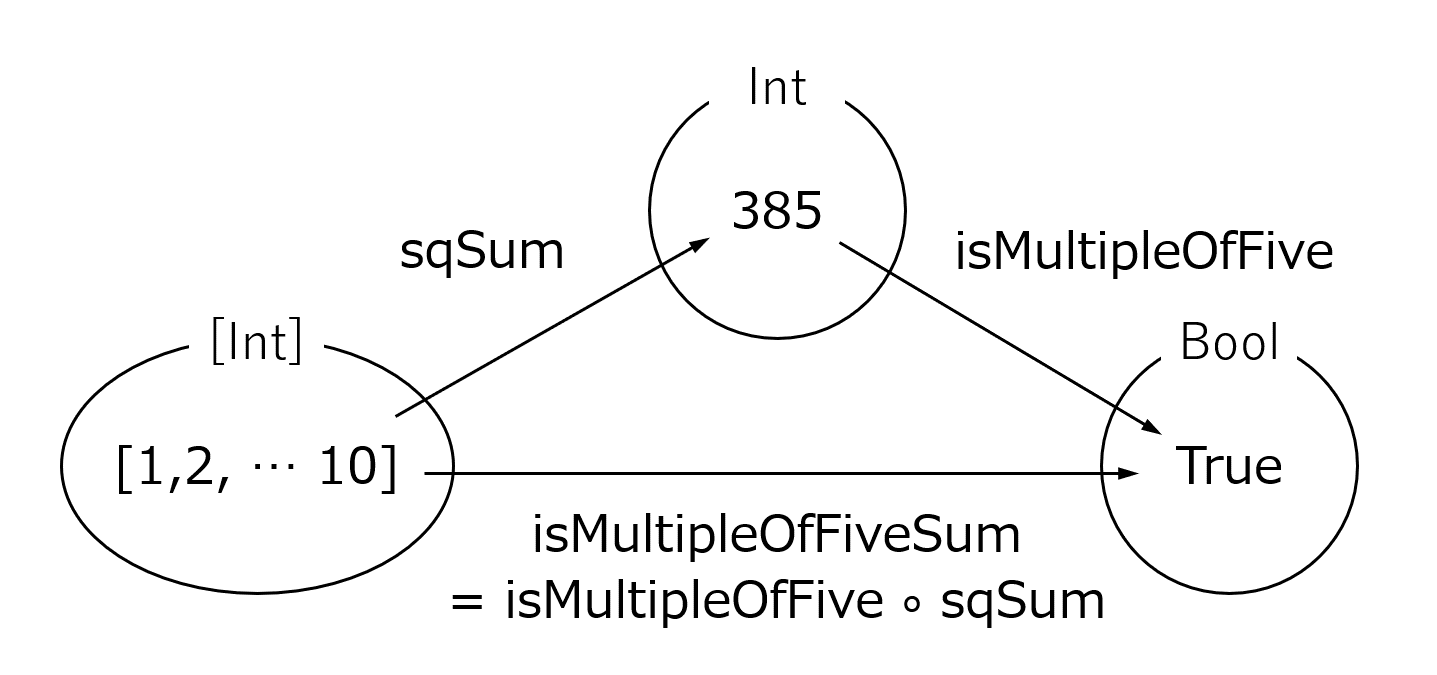
ポイントは sqSum の値域と isMultipleOfFive の定義域がぴったりと重なっていることです⁴。もし sqSum で変換した値が isMultipleOfFive の引数になり得ないときはエラーが発生してしまいます。このようなことができるのも、関数の型宣言の時に、それぞれの関数の定義域と値域を明示したからなんですね。

ちなみにですが、 isMultipleOfFiveSum の定義にはポイントフリースタイルを使用しています。
Haskellでは、条件を満たせば関数の定義でも引数を省略することが可能です。

isMultipleOfFiveSum = isMultipleOfFive . sqSum          -- これ（ポイントフリースタイル）と
isMultipleOfFiveSum xs = (isMultipleOfFive . sqSum) xs  -- これが同じ

これがまさに数学でいうところの $f \circ g$ と同じです。数学で「関数」というと $f(x)$ を想像することがあるかと思いますが、実際は $f$ の部分だけで、 $f(x)$ は $f$ によって $x$ を写した値、つまり値域の要素を表現しています。
Haskellの関数合成も、具体的な引数を与えることなく、関数のみで合成を定義できるというのはスマートですね。

おわりに

Haskellと数学の類似点を挙げてきましたが、当然ながら私も最初から見分けられたわけではありません。関数型言語というものも、他のプログラミング言語でも関数は出てくるのに、なぜわざわざ「関数型」と呼ぶのかわかりませんでした。ある日突然、関数型言語の「関数」という言葉が数学の文脈であることに気付いたことで、霧が晴れたかのように理解が進みやすくなったような感覚です。

有名なすごいH本の「型クラス」の項に次の注釈があります。

型クラスはオブジェクト指向のクラスとは同じではないということに注意してください。これは重要です。

ここで言う「クラス」も、数学に登場するクラスのことを指しているのではないかと考えると、違和感は無いような気がします⁵。

もしHaskellを学びたいと感じていて、かつ数学が得意だという方がいるのであれば、プログラミングより数学の頭で考えることで理解が進みやすくなるかもしれません。もちろん、数学ができなければHaskellができないと言っているわけではありません。論理において逆や裏との真偽は必ずしも一致するとは限りませんので。
この記事がこれからHaskellを学ぶ人の理解に少しでも役に立つのであれば幸いです。

明日は @YOMOGItaro さんより、NSX関連のお話です。お楽しみに。

記事の内容を理解する必要はありません。ただリンク先を開き、Ctrl+fでletとwhereを検索すれば良いのです。 ↩
プログラミングで関数といえばサブルーチンを指す場合があり、私はこれと混同していたため「関数型言語」という言葉を理解するのに時間がかかってしまいました。数値以外も扱いますし、個人的には写像型言語とでも呼んでもらった方が区別できてわかりやすいと思います。 ↩
とはいえこの定義が明示的に書かれることはあまりありません。もし仮にここに無限の余白があったとしても、実数は不可算無限個あるので全て書き並べることは不可能です。 ↩
数学の合成関数では完全に一致している必要はありませんが、 $f \circ g$ の場合は ( $g$ の値域 ) $\subseteq$ ( $f$ の定義域 ) である必要があります。 $g$ がどんな値に写しても、 $f$ の守備範囲でなければなりません。 ↩
私は集合論の公理といえばZFC公理系しか知らず、かつその公理体系ではクラスは厳密に存在しないらしいので、厳密にクラスというものを理解しているわけではありません。ただ何となくですが、共通の性質を持つ型の集まりという意味で型クラスとよび、そのうちの一つ一つの型をインスタンスと呼ぶことにはそれほど違和感はありません。 ↩