WA* は、A*をほんの少し変えることで「上限付きの」非最適解を返すことの出来るやり方です。
Pohl, Ira (1970). "First results on the effect of error in heuristic search". Machine Intelligence 5: 219–236.
GBFSの欠点
前回紹介したGBFSの欠点は、解の 質 、つまり探索経路の長さ/コストについての保証が全くないことです。最適解のコストがどれだけ小さいとしても、GBFSはいくらでも大きなコストの解を返す可能性があります。
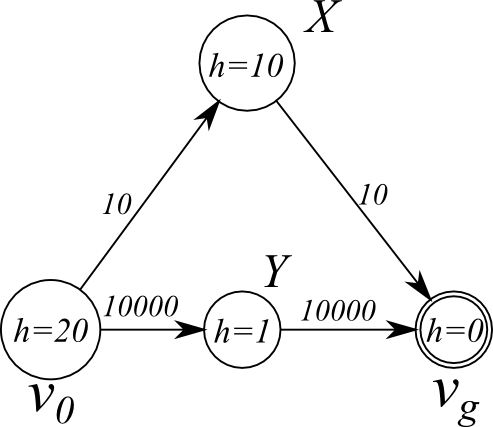
例えば次のグラフを見てみましょう。このグラフでの最適コストは、上のノードXを通るコスト20の経路です。しかし、GBFSはノードYを通るコスト20000の経路を返します。これは、GBFSがヒューリスティクス $h$ を信頼しすぎるからです。
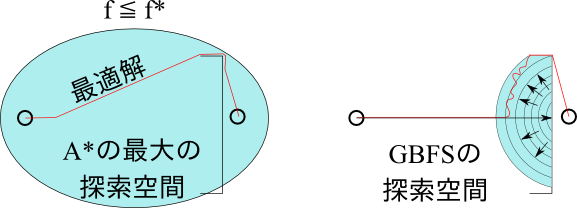
GBFSは、ヒューリスティクスの質が良ければよいほど素早く解を見つけるという点ではA*と変わりありません。しかし、この図の $h$ は admissible かつ consistent です。そのうえ、特に $X$ を通る方の経路では、 $f=f^*$ であるパーフェクトなヒューリスティクスになっています。このことから、GBFSは ヒューリスティクスの質がいくら良くても 悪い解を見つける可能性があることがわかります。
上限付きの非最適性
一方WA* , Weighted A* は、GBFSとは異なり、ある程度の最適解の質の保証をもちます。
Aが $f=g+h$ を、 GBFSが $f=h$ を採用したのと同様に、 WAは ある重み $w$ の元で $f=g+w\times h$ を用いてノードを展開します。これは、 今までの距離 $g$ に対して $h$ を $w$ 倍信頼する と解釈することが出来ます。そして、WAの返す解のコストは、 Aの返す最適解のコストの $w$ 倍以内であることが示されます。
| アルゴリズム | $f$ 値の定義 |
|---|---|
| A* | $g+h$ |
| GBFS | $h$ |
| WA* | $g+w\times h$ |
AがWAの$w=1$ のケースであること、およびGBFSが WA* の $w \rightarrow \infty$ のケースであることがわかるでしょうか。これは、ちょっとした式変形をすればすぐわかることです。
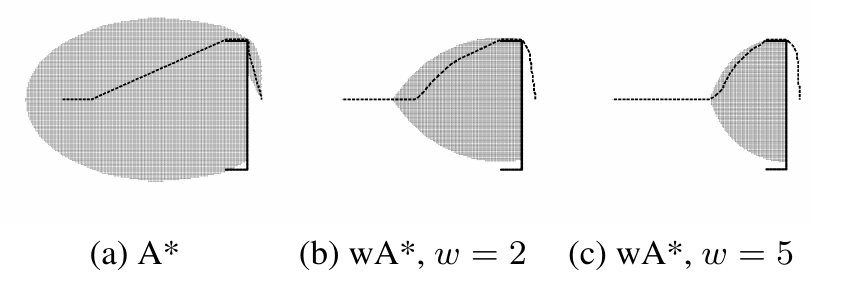
WA* の探索空間を前回同様可視化すると以下のようになります。 $w$ が大きくなればなるほど、前回お見せしたGBFSの探索空間に近づいていくことがわかります。
発展: WA* の問題点
WA* の問題点は、 どんな$w$ なら十分役に立つのかを問題を解く前に知ることが出来ない点 です。
小さすぎる$w$で探索を始めたら、探索空間が依然として大きすぎ、解を求めるのに要する時間がまだまだ長すぎるかもしれません。たしかに、必要な時間はA*よりは短いでしょう。しかし、例えば2500万年が6年になったとして、どれぐらい嬉しいでしょうか? せいぜい、お姉さんがロボットにならなくてもよくなるぐらいの差しかないでしょう。
一方で $w$ を大きく取り過ぎてしまえば、解の質の保証という利点が失われてしまいます。例えば、 $w=1000$ として最適解の1000倍までの解を許すことにどれだけ意味があるでしょうか (もちろんこれは、グラフ探索を何のために使っているかという状況に応じて変わります)。
この問題を別の言葉でいいかえれば、 WA*には パラメータチューニング の問題がつきまとうということです。 ここで $w$ の最大値はGBFSに相当する $\infty$ です。このため、この古典的なアルゴリズムを基礎として、 Anytime Algorithm、すなわり$w$ の値を動的に変化させる適応的なアルゴリズムが複数考えられています。そのお話はまた今度。