今日は GBFS, Greedy Best First Search を紹介します。

完全性を保った非最適探索

前回触れた山登り法は、 解が存在するときにきちんと解を返してくれる保証 がありません。この保証のことを完全性と言います。_{完全と呼ぶ派と完備と呼ぶ派とがあるらしいですが、completeの訳なので正直どっちでもいいです。} 単純な山登りには、$h$ の極小点とゴールが一致するなどの特殊な状況を除き、完全性がありません。

一方でA*やダイクストラには完全性があります。完全性があるので、解が存在すればかならずいつかは解を発見できます。しかし、「いつか」というのはどのくらいの未来のことを指しているのでしょうか? この質問は、すでにある人が体を張って示してくれています。

私は皆に「組み合わせ爆発のすごさ」を教えたいの！止めないで！

みなさんもご存知の通り、指数爆発を起こしている探索問題を工夫なしに解こうとすると、スパコンを使っても何千万年もの時間がかかるわけですね。特にダイクストラはそのような種類のアルゴリズムです。それだけではなく、A*に優れたヒューリスティクスを組み合わせたときであっても、全く探索が終わらないような場合が存在します。実用的なグラフ探索を行いたいという場合には、これではこまりますね。

「素早く探索をしたい」「完全性も保ちたい」「両方」やらなくっちゃあならないってところが研究者の辛いところです。でも、じつはいい手があるんです。

GBFS

GBFSは、 $f=h$ とし、 $g$ 値を無視する A* です。優先度付きキューにノードをf値に従って挿入する点は変わりません。

GBFSは、探索にあたって $h$ を完全に信頼するアルゴリズムだと言えます。一方、A*は今までの経験 ($g$) と予測 ($h$) を同程度に重視するアルゴリズムだといえましょう。

GBFS は完全です。 $h$ が小さいところを優先して探索するのはかわりませんが、キューにいままで展開した経路が残っているので、最も$h$ が小さい範囲で失敗したらきちんとバックトラックします。仮に$h$ が完全にでたらめな値を返す関数であっても、十分な時間があれば探索空間を全て探索し尽くすことで解を見つけられます。また、A*/ダイクストラと同じく重複検知を行うので、巡回路にハマって永遠にループすることもありません。

GBFS の挙動

GBFSは、名前の通り Greedy に探索を行います。このことを、下の図を用いて検証してみましょう。

例として扱う問題は、 4-connected grid でロボットが目的地まで移動する問題だとします。目的はスタートからゴールまでの経路探索です。ただし、このフィールドにはおわん型の壁があり、ロボットは壁を乗り越えられないものとします。ヒューリスティクスとしてユークリッド距離を用います。

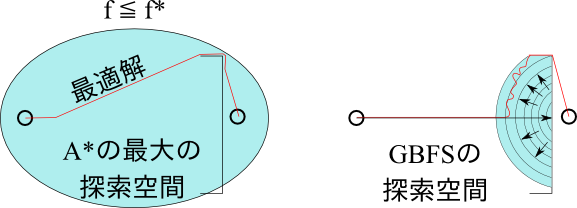
左がA*の探索空間だとすると、GBFSの探索空間は右図のようになります。実験的には、この探索空間を全て探索するわけではないのですが、イメージとしてはこれで十分でしょう。

実験するとA*はこんな感じ。 (Likhachef 2008 R* Search より拝借)

GBFS の欠点

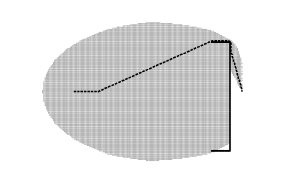
GBFS の欠点は、解の長さに全く上限がないことです。先ほどの図でもわかるとおり、GBFSの返す解は最適解よりもだいぶ長くなります。あまりにも長い解は、いくら探索が早くても使い物になりません。

GBFSのもうひとつの欠点は、 $h$ を信頼しすぎてトラップにかかりやすい点です。先ほどの図の $h$ が正しい領域、例えば壁よりも右側での領域では、GBFSは一直線にゴールに向かうことができます。しかし壁よりも左側では、GBFSはおわん型のトラップにハマってしまい、A*と同じく半円状の広い空間を探索していることがわかります。

一方A*は、たとえ壁を越えたとしても一直線にゴールへ向かうことは出来ません。これは、A*が壁の右側にしっぽのような狭い楕円形の探索空間を形作っていることからもわかります。

まとめ

GBFSを紹介しました。次回はGBFSの一つ目の欠点、「解の長さに上限がない」ことを解決するアルゴリズムを紹介します。