みなさんお久しぶりです。
発表のためにAAAI-16に来ています。知らない人も多いかと思いますが、IJCAIとならび、AIの国際学会で最も難関と言われる学会です。個人的には自分もA*の改善論文でPaper Award 密かに狙っていたのですが、Bidirectional Search 論文に取られてしまいました。自分の論文の内容はこんどまた書きます。自分の発表は昨日終わりました。
AAAI-16 Best Paper Award Bidirectional Search that is Guaranteed to Meet in the Middle. Holte, Felner, Sharon, Sturtevant
朝ごはんのあとに思いつきで書いてるだけなので、そんなにくわしくは書きません。
この論文は、探索ノードを$n$として、OPENリストのソートに以下の値を用いる MM (Meet in the Middle) というアルゴリズムを提案しました。
pr(n) = \max ( g(n)+h(n) ,\; 2g(n) )
$g(n)+h(n)$ は A* の $f$ 値と同じ定義です。
超シンプルですが、これを用いることで、以前書いた ProveOptimality の必要がないBidirectional Searchを実現することができます。つまり、Bidirectional Searchとしては初めて、A*と同様に、最初に見つかった解がそのまま最適解であることが保証されるアルゴリズムです。
最初に提案されて50年もたっていまさらかよと思われるかもしれません(というか自分も同感です)が、まあ「人気が落ちてしまった分野が再発見されて研究が進む」というのはよくあることですね。
以前の記事にも書いたように、Bidi Search は Brute ForceではAより強く、Strong Heuristicsでは Aに負けるのでした。この性質はMMでも引き継がれます。
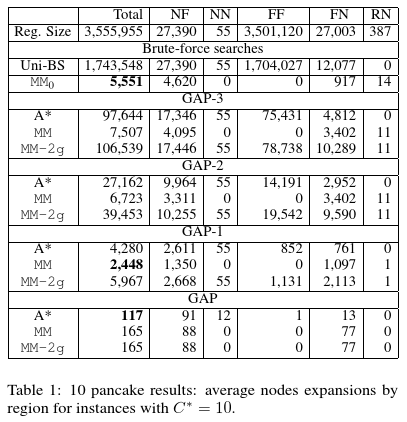
特に、MMのうち、A*に対するDijkstra Search, つまり $h=0$ のケースを $MM_0$ と呼ぶことにします。すると、 $MM_0$ は Dijkstraよりもかなり早く探索を終えることができます。
Brute-ForceだとUni-BS(Unidirectional Brute Force = dijkstra) よりも $MM_0$ がはるかに早いですね。一方、おそらくGAP-3からGAP-1になるにつれてより正確なヒューリスティック関数を用いているのだと思います。正確なヒューリスティックがあればA*が早く、不正確だとやはりMMが早いようです。
追記: なお、 MM-2g は $\max(f+g, 2g)$ の $2g$ をなくして、$f$ のみを用いる普通のBidi Searchにしたもののようです。これだと、ProveOptimalityが必要になることで、必要な探索ノード数が増えていることがわかります。
以上、アリゾナ、フェニックスからお届けしました。ちなみに日中は29度とかになって暑いですが、朝は気持ちいいです。
PS. あっ、記念写真です。