A* (1968)

東京大学大学院 総合文化研究科、福永研究室の浅井です。
続いて、探索の高速化に必須の手法、A* (エースター) を紹介します。

Aは「ヒューリスティック探索」とか「発見的探索」と呼ばれます。この名前が悪くて、おかげで、酷い誤解を受けています。例えばあるスライドでは、Aは「近そうなところから探索」と書かれています。なんか適当に探索するかのような印象ですね。A*は、ダイクストラ法を拡張し、 理論的裏付けを持った下界を用いてグラフを探索するための手法 です。

Dijkstra法 の何がタコか

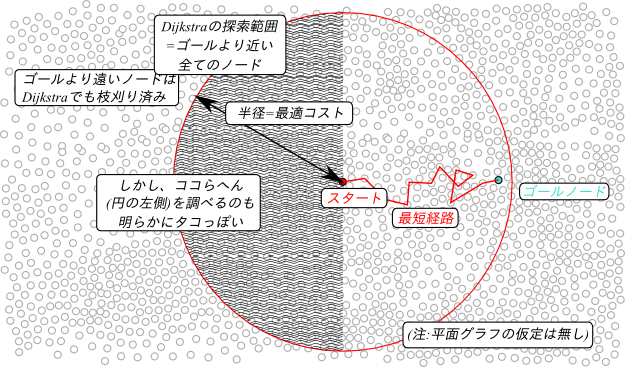
Dijkstra法は、最適解を見つけることができるので、グラフ探索において幅優先や深さ優先よりははるかにタコ度が低いのですが、それでもまだ実用性に乏しいほどタコです。次の図を見てください。

ダイクストラ法の探索する範囲は、スタートからの距離がゴールまでの最短距離以内の領域全てです。
その領域には、ゴールと全く関係のない ≒ ゴールから遠ざかるようなノードも含まれています。
ノードの数が指数的に爆発しているグラフでは、このような無駄な空間も指数的に沢山あるので、
ダイクストラ法では全く歯が立ちません。
たとえば、4x4x4のルービックキューブ。正しくは、名前を Rubik's Revenge と言います。

こいつの面の組み合わせ、すなわち探索空間は、だいたい $7\times 10^{45}$ こあります。仮に面1つが 1バイトで表されたとして、この探索空間(グラフ)をどこかに保存するとすれば $7\times 10^{21}$ ゼタバイトもの容量を必要とします。この規模の容量は、仮に地球上の全ての一時記憶、二次記憶を集めても足りません。参考:2010年の全世界のデータ送料は数ゼタバイトであるという調査結果があります。 ちなみに、5x5x5のキューブ(Professor's cube) は $2.8\times 10^{74}$ 個の組み合わせがあります。

仮にこのうちダイクストラでかなりの空間が削減できたとしても、未だに莫大な数の探索ノードが残っています。では、どうすればこのようなグラフでゴールを探索できるのでしょうか?

A* (Hart, Nilsson, 1968)

答えは、「スタートからの距離」だけでなく「ゴールまでの距離」も考えることです。
スタートからの距離と、ゴールまでの距離の和を取ることで、探索すべき空間を楕円の範囲に制限することが出来ます。(以降、距離と書いたりコストと書いたりしますが、どちらも同じ意味です)

　$|v_0-v|+|v_g-v| \leq$ 最適コスト

$|v_0-v|$ はスタートノード $v_0$ から探索ノード $v$ までの距離、
$|v_g-v|$ はゴールノード(注:未知) $v_g$ から $v$ までの距離を表しています。

伝統的なAIの教科書(e.g. AIMA)では、ノード$n$が最適経路上にあるとき、

• スタートから$n$までの最適コストを $g^*(n)$
• $n$からゴールまでの最適コストを $h^*(n)$
• 両者の和である、経路全体の最適コストを $f^*(n)$

と表記します。以降、こちらの表記を用います。

ダイクストラ法の一般化

ダイクストラ法は、幅優先探索に加えて、ノードをpriority queueに入れるところが重要でした。そして、キューに入れるときのノードの優先度は、その時点で知られているスタートからの最小コストでした。

先ほど説明した楕円の文脈では、この「スタートからの現時点の最小コスト」は直接 g*(n) に関係します。ただし違うのは、この「現時点で知られている最小コスト」というのは「最適コストg*」とは異なるということです。そこで、「現時点で知られているコスト」を、「*」のない(最適ではない)コストということでg(n)と表記します。

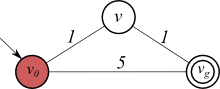
「現時点で知られている最小コスト」g(n)は、探索が進むに連れ真の最適コストg*(n)に上から近づいていく値、上界値です。例えば、前回使ったこの図を振り返りましょう。ダイクストラ法において、$g(v_g)$ は、探索開始時では$\infty$です。$v_0$が展開されて$g(v_g)$は 5 になりますが、$v$の展開後は2に更新され、これが最短コストでした。

Aは、キューに入れる際、$g(n)$ではなく$g(n)+h(n)=f(n)$ を用います。g(n)がg(n)に上から近似してゆく値だったのと同様に、$h(n)$は h*(n) を、$f(n)$は f*(n) 近似してゆく値です。ただし、$h(n)$ は 真の値を下から近似する値、下界値です。

ここで、ダイクストラは A* の $h(n)$ を0に固定したものだと考えられます。ダイクストラ法は全ての辺のコストが0以上であることを仮定しているので、経路のコストの和も0以上です。すなわち、0 は必ず h* の下界になっています。

問題固有の知識(ヒューリスティック関数$h$)を用いた探索

一方、ある種の問題に対しては、問題空間にかせられた制約を用いて、h*の下界値 h を、0よりも良い精度で計算することが出来ます。一般に、関数h(n)をヒューリスティック関数とよび、h(n)は一定の問題種別ごとに定義されます。もちろん、異なる仮定を有するグラフに対しては、同じヒューリスティック関数を使うことが出来ません。

一例として、カーナビの経路探索を考えてみましょう。入力のグラフは、ノードにxy座標が乗っていて、どの辺のコストもその辺の長さ(ノード間の直線距離距離)と等しいと仮定します。

このようなグラフでは、三角不等式が満たされるので、どの離れた2つのノードをつなぐ経路の和も、その直線距離よりも長いことが証明できます。(経路から一個ずつノードを減らしていって、直線距離に繋ぎかえれば容易に証明できます) 従って、hを例えば以下のように定義すれば、それは常に h* よりも小さい値を取ることが言えます:

$h_{v_g}(n)=\sqrt{(v_{gx}-n_x)^2 + (v_{gy}-n_y)^2 } \leq h^*(n)$

上の図の実際の$v_g$の座標を代入すれば、下のようになります。

$h(n)=\sqrt{(560-n_x)^2 + (261-n_y)^2 } \leq h^*(n)$

この関数はもちろん、(前提1) ノードにxy座標が乗っていて、 (前提2) どの辺のコストもその辺の長さ(ノード間の直線距離距離)と等しい グラフにしか使えません。但し、この$h$は、今$v_g$を代入したように、特定のゴールに依存しているわけではありません。言い換えれば、この$h$は問題には非依存 だが ドメイン依存 な関数と言えます。

様々な探索問題に対し、様々なヒューリスティック関数が開発され、真のコストの下界であることが証明されています。探索を扱う人工知能分野では、より正確な(見積もり値の高い)下界関数を設計し、探索を高速化した、という形で論文を書くことが出来ます。(もちろん、性能評価付き。)

用いる関数が出す見積もり値が正確であればあるほど、必要な探索空間が狭まる傾向にあります。一例として、下の図を見てください。見積もり値$h$が正確であればあるほど、探索空間が狭まることがわかります。2つの関数 $h_1,h_2$について、全てのノードに対して$h_2$がより正確な値を返す場合、$h_2$は$h_1$を抑える(dominate)と言います。そのような証明が出来ない場合、2つは比較不能(incomparable)といいます。

「常に正しい見積もり値hを返す」仮想的なヒューリスティクスのことを「パーフェクト・ヒューリスティクス」と呼びます。hは全てのヒューリスティクスを抑えています。h*は仮想的なアイディアですが、問題によってはパーフェクトであるようなヒューリスティクスも存在します。例えば、xy方向の4結合正方格子(縦横に繋がった格子, 4-connected grid map)のグラフの探索では、マンハッタン距離はパーフェクトです。

次に、「常に0を返すヒューリスティクス」 $h_0$ (ダイクストラ法の用いるもの) を、 blind ヒューリスティクスと言います。 全てのヒューリスティクスはblindを抑えます。

もうひとつ重要な知識は、2つのヒューリスティクスの最大値を返すヒューリスティクス $max(h_1,h_2)$ が、元の2つを共に抑えるという点です。2つ以上のヒューリスティクスを組み合わせる手法もよく研究されています。

A*

最後に、具体的にアルゴリズムを書いておきましょう。ダイクストラ法との差分はほとんどありません。キューに追加する時の値が$f$になるだけです。

1. Let $OPEN$: a priority queue.
2. Let $n \in V; h(n): V \rightarrow \mathrm{R}$ : a heuristic function
3. Initialize: $push(v_0,f(v_0),Q)$ 　 /* note: $f(v_0)=g(v_0)+h(v_0)=0+h(v_0)$ */
4. Until $empty(OPEN)$
   • Let $v \leftarrow popmin(OPEN)$ 　　/* (注: tiebreaking) */
   • $push(v, CLOSE)$ 　　　　　　/* or mark CLOSE */
   • When $v = v_g$ then return $reverse(unfold(parent, v_g))$
   • Else, for each $v' \in children(v)$ do
     • Case $v' \in CLOSE$
       • If $g(v) + cost(v,v') < g(v') $
         • $update(v',v)$
         • $remove(v', CLOSE)$
         • $push(v',f(v'),OPEN)$　　/* reopen node */
     • Case $v' \in OPEN$
       • If $g(v) + cost(v,v') < g (v')$
         • $update(v',v)$
         • $remove(v', OPEN)$
         • $push(v',f(v'),OPEN)$　　/* reinsert node */
     • Otherwise, always
       • $update(v',v)$
       • $push(v',f(v'),OPEN)$　　/* open node */

• return nil

ただし、 $update(v',v)$ は

• $g(v')\leftarrow g(v) + cost(v,v')$
• $parent(v') \leftarrow v$

です。