Modelling OR Approach in Lisp

16日にLispMeetupで話した内容のまとめです。後半の内容はMeetupで詳しく話せなかった内容。

背景

世の中には様々な制約充足問題/最適化問題があり、それぞれに速いソルバ (State of the Art) があります。それぞれの問題自体についての解説はWikipediaなどで調べてもらうとして、例えば:

• SATソルバ -- Glucose, Lingeling -- 過去の SATRace Competition で優勝したソルバ達
• IP/LPソルバ -- ILOG CPLEX, Gurobi -- いずれも商用ソルバ
• 制約充足問題ソルバ (Minizinc ソルバ) -- Minizinc Challenge 参照
• ASP (Answer Set Programming -- 解集合プログラミング) --- ASPCOMP 参照
• Prologエンジン -- SWI-Prolog, XSB, YAP, B-Prolog
• SMTソルバ -- SMT-LIB solvers 参照

ソルバを書いてる人はむっちゃヤバくて、ソルバもなんかヤバイです(語彙不足)。
Lisperだと「おらいっちょ作ってみっか」と自分でソルバを書き始めがちで、
実際生産性が高いので時にはそれでうまく行くことも多いのですが、
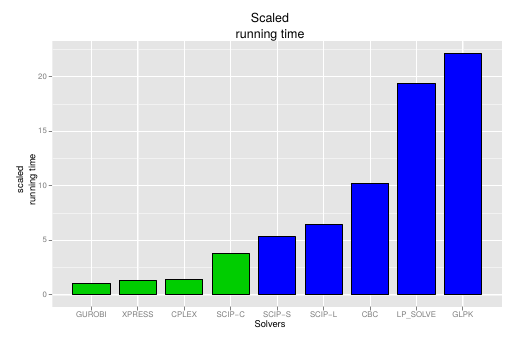
これらのソルバは、企業でフルタイムで働くその道のプロや、その分野で30年やっている大学教授によって書かれていることがままあります。以下の図は ¹ より引用。 緑が商用ソルバ、速すぎる・・・

まあ、速いSATソルバなどを作ること自体が目的の場合にはLispで書いてもいいのですが、
ソルバを使って素早くアプリケーションを書く場合には、いちいち自分で作っている時間はありません。

例にもれず私も、これらのソルバのユーザに該当する人間です。
私は古典プランニングという問題のソルバ (プランナ) を開発していますが、
この問題では沢山の 内部で上記のソルバを呼び出す 手法があります。
これらは、「解きたい問題を別のソルバの入力言語に変換し、高速なソルバで解き、その解をデコードする」という、近年の研究動向²にそったものになっています。

• プランニング問題をIP/LPに変換して解く。 (JAIR 2005)
• プランニングでの状態の評価関数をIP/LPに変換して計算。 ほかにも同様の手法多数
• SATPLAN --- プランニング問題をSATに変換して解く方法の元祖。 Planning as Satisfiability, Henry Kautz and Bart Selman, Proceedings ECAI-92.
• Temporal Planning (== スケジューリング) をSMTに変換して解く。
• プランニング問題のパースと前処理にDatalogプログラムを構築 (Datalog: Prologのサブセット)

したがって、いざプランナを書こうとなったときに、 これらのソルバを呼び出すことが 朝起きて食パンをトースターに放り込めば焼けるっていうぐらい簡単 になっていれば、プランナを書くのがもっと 楽しく かつ 楽 になるにちがいありません。³

CL-SAT, CL-PROLOG, CL-SMT

そういうわけで、将来的には上に挙げた全ての言語に対してLispからのAPIを構築することを念頭に、
手始めに CL-SAT, CL-PROLOG, CL-SMT を作りました。

(ql:quickload :cl-sat.minisat)
(ql:quickload :cl-sat.picosat)
(ql:quickload :cl-sat.glucose)
(cl-sat:solve '(and (or a b) (or a !b c)) :minisat) ; :picosat,:glucose にかえるだけでソルバが変わる
; ->
; (C A)       ----- A:true, C:true が解
; T
; T

(ql:quickload :cl-prolog.swi)
(ql:quickload :cl-prolog.bprolog)
(ql:quickload :cl-prolog.yap)
(cl-prolog:run-prolog 
 `((factorial 0 1)
   (:- (factorial ?n ?f)
       (and (> ?n 0)
            (is ?n1 (- ?n 1))
            (factorial ?n1 ?f1)
            (is ?f (* ?n ?f1))))
   (:- main
       (factorial 3 ?w)
       (write_canonical ?w))
   (:- (initialization main)))
  :swi) ; or :yap, :bprolog
; ->
; "6"

; Prolog プログラムとしては以下と等価:

factorial(0,1).
factorial(_n,_f) :-
    _n > 0,
    _n1 is _n-1,
    factorial(_n1,_f1),
    _f is _n * _f1.

main :- factorial(3,_w),write_canonical(_w).

:- initialization(main).

(ql:quickload :cl-smt.cvc4)
(ql:quickload :cl-smt.yices2)
(ql:quickload :cl-smt.z3)
(cl-smt:solve
   '((set-option :produce-models true)
     (set-logic ^QF_LIA)
     (declare-fun x () |Int|)
     (declare-fun y () |Int|)
     (declare-fun z () |Int|)
     (assert (and (or
                   (<= (+ x 3) (* 2 y))
                   (>= (+ x 4) z))))
     (check-sat)
     (get-model))
    :cvc4) ; or :yices2, :z3
; ->
; (sat
;   (model
;   (define-fun x () int (- 3))
;   (define-fun y () int 0)
;   (define-fun z () int 2)))

例: PDDL のグラウンディング

せっかく作ったのだから、使わないと損です。そこで、いまやっている、プランニング問題の前処理に必要な、 一階述語論理の命題論理化(grouding) にprologを使ったコードを見せます。

プランニング問題

プランニング問題は、 初期状態 $I$ に アクション $a\in A$ を適用して ゴール条件 $G$ を達成する方法を探す問題です。 ゴールに到達するのに使われたアクションの列 $(\ldots a_i \ldots)$ を プラン といい、これが問題の答えになります。

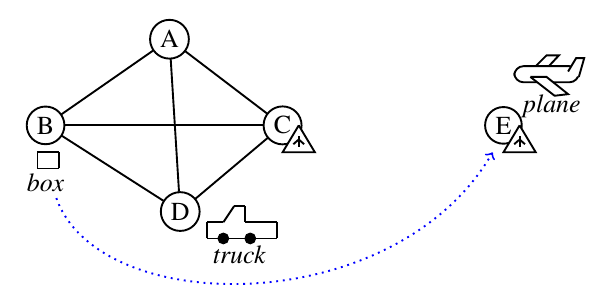
たとえば、以下のような簡単な輸送問題(Logistics)を考えることにします⁴。図に示されている状態が $I$ で、 ゴール条件は 地点E に box があることです。

それぞれの 状態 は、一階述語論理で書かれた命題の集合です。例えば上の問題は以下のような感じで記述でき、初期状態は :init の中に書かれています。(一部省略しています) このような定義を行うDSLを、PDDL (Planning Domain Description Language) と呼びます。

(define (problem logistics)
  (:init
   (connected a b)
   (connected b a)
   (connected a c)
   ...
   (connected c d)
   (airport c)
   (airport e)
   (box box)
   (truck truck)
   (airplane plane)
   (at truck d)
   (at box b)
   (at plane e))
  (:goal
   (at box e)))

上の定義は 問題の定義 しか行っていません。アクションの定義は ドメイン定義 で行います。
以下のアクションは、 変数 ?box, ?truck, ?location について、前提条件(precondition) としてそれらが同じ場所にいるときには、 pickup アクションによって ?box を ?truck に運び入れることが出来ることを指しています。運び入れることで 効果(effect) として 命題 (in ?box ?truck) がtrueになり、また (at ?box ?location) の値が false になります。

(define (domain logistics)
  ...
  (:action pickup :parameters (?box ?truck ?location)
   :precondition (and (truck ?truck) ; 前提条件
                      (box ?box)
                      (at ?box ?location)
                      (at ?truck ?location)) ; --- truck と box は同じ場所にいる
   :effect (and (not (at ?box ?location)) ; 効果
                (in ?box ?truck)))
  ...)

このようなアクションが他にも沢山あり、例えばこのドメインでは、飛行機を飛ばす fly アクション、 トラックが移動する drive アクションなどが考えられます。

グラウンディング

さて、ゴールを探すためには、逐一アクションを状態に適用して、それがゴールであるか、あるいはゴールに近づいているかなどをチェックしながら探索を行います。この問題は従って アクションが辺、状態がノードのグラフ探索問題 になっています。

しかし、それぞれのノードで 変数に入れられる引数を毎回探して、リストを構築する ようなやり方では遅すぎます。より効率的な、配列アクセスを行うための適切なデータ構造が必要です。

ここで、 グラウンディング が必要になってきます。グラウンディングを一言で言えば、アクションや述語について、可能な引数の組合せを予め列挙しておくことです。はじめに列挙しておけば、全部で何個のインスタンスがあるのかがわかり、ただのbit配列として扱うことができます。例えば at 述語について、 trueになりうる 引数の組合せは:

(at truck a) (at truck b) ... (at truck d) ; truck は e には行けない
(at box a)   (at box b)   ... (at box e)
(at plane c) (at plane e)

と、最大11個しかありません。このように、 命題が trueになりうる ことを reachable といいます。

Reachability Analysis

結果として得られる配列の長さは reachable な命題の数と等しくなるので、その数は小さければ小さいほどメモリ使用量が減ります。したがって、単純に考えれば reachable な命題のみを列挙すればいいと思うかもしれません。

残念なことに、そのような full reachability analysis は 問題を解くこと自体と同じぐらい難しいです。
例えば、 (at box e) は reachable でしょうか? (at box e) が問題のゴール条件だったことを思い出しましょう。 (at box e)のreachabilityを示すのは、問題の解の存在を示すのと等価です。 ちなみに、プランニング問題の充足可能性(解の存在)問題は PSPACE完全で、これはNP完全問題よりも少なくとも同等以上に難しい問題です (NP⊆PSPACE)。NP以上なので基本的に指数爆発。

そこで、full reachability ではなく、 元の問題よりも制約が緩い問題、 緩和問題を解くことを考えます。緩和問題を考えることで、 reachable な集合を部分集合に含む、すこし大きい集合を見つけます。今回は、 命題をfalseにする効果を無視する緩和: 削除効果緩和 を使います。そしたら、命題は追加されるばっかりなので、これ以上増えなくなるまで追加すればアルゴリズムが止まります。 この緩和問題の中でreachableであることを、 relaxed reachable といいます。

relaxed reachable な命題を列挙するのに、 Datalog プログラムを使います。
まず、初期状態でtrueであるような組合せはすでにreachableです。
次に、全ての前提条件が満たされた場合、追加効果 (trueにする効果) の対象になる命題が reachable になります。これを cl-prologで表現すると、以下のようになります。述語 (at ?x ?y) は (reachable at ?x ?y) に変わりますが、これは prologの組み込み述語などとconflictしないようにするためです。

(run-prolog
 (append
  ;; initial facts
  (iter (for proposition in *init*)
        (collect `(reachable ,@proposition)))
  ;; facts
  (iter (for a in *actions*)
        (ematch a
          ((plist :precondition `(and ,@precond)
                  :effect effects)
           (dolist (e effects)
             (collecting
              `(:- (reachable ,@e)
                   ,@(iter (for pre in precond)
                           (collect `(reachable ,@pre)))))))))
  ;; output facts
  (iter (for predicate in *predicates*)
        (collecting
         `(:- main
              (reachable-fact ,@predicate)
              (write "(")
              ,@(iter (for e in predicate)
                      (unless (first-iteration-p)
                        (collect `(write " ")))
                      (collect `(write ,e)))
              (write ")\\n")
              fail)))
  `((:- main
        halt)))
 :bprolog :args '("-g" "main"))

ここのコードは、cl-prologがうごいていたため15分ぐらいで書くことができました。感謝myself!

まとめ

以上、さまざまなソルバへのAPIがあれば、上司や査読者を気にせずに楽しく問題を解けるということがわかりました。正直、NP完全以下の組合せ論的問題であれば、実務的には わざわざ特化ソルバを書くよりは、SATエンコーディングやILPで解いてしまった方がいいと思ってます⁵。まあ、その場合でも、どのエンコーディングを用いるかによって求解の速度が変わるので⁶、一概に簡単とも言えないし、またおそらく特化ソルバの方が速い場合もあると思いますが。

脚注

1. Meindl, Bernhard, and Matthias Templ. "Analysis of commercial and free and open source solvers for linear optimization problems." Eurostat and Statistics Netherlands (2012) ↩

2. http://bach.istc.kobe-u.ac.jp/aisat.html ↩

3. またこれらのソルバを使うことには、楽であることや速いことのほかにもう一つのメリットがあります。それは、「 お墨付き のソルバを使うことで、ソルバ部分の性能や実装の正しさに関して(査読者や上司に)疑りの目をむけられることがない」ということです。たとえば、プランニングソルバの内部で使う為に自前のSATソルバを書いたとして、査読のたびに「そのプログラムが正しい解を出していること、検証した?」とか、「そのSATソルバ、あのソルバより遅いんじゃないの?」(全体としてのプランニングソルバの性能とは関係の無い質問)などと言われるのは、避けたいですよね。 ↩

4. Landmark-Based Heuristics and Search Control for Automated Planning, Silvia Richter, Ph.D Thesis ↩

5. そのような理由で、自分はいわゆるプロコンみたいなのには興味がありません。超ムダに見える ↩

6. SATソルバーの最新動向と利用技術, 宋 剛秀, 田村 直之, 神戸大学情報基盤センター ↩