許容的なヒューリスティクスよりも少し強い仮定として、 無矛盾 なヒューリスティクスというクラスのヒューリスティクスがあります。Consistentの訳ですが、Monotonicとも呼ばれるので、 単調な ヒューリスティックと訳してもいいのかもしれません。しかし、その意味するところは 無矛盾 のほうがわかりやすいかもしれません。個人的には、Consistencyの訳は 「一貫した」とか、「整合性」とか、いうのもあり得ると思うのですが、AIMAの日本語訳でこの訳が用いられているので、このバージョンを用います。
無矛盾でない (inconsistent) ヒューリスティクスを人間で例えると、言うことがコロコロ変わる信頼の置けない奴という意味です。ここを実感していただくために、まず、無矛盾なヒューリスティクスの定義と「単調」の意味を示して、それから「無矛盾」の意味を解説します。
「無矛盾」なヒューリスティクス : Consistent / Monotonic heuristics
Consistency of a heuristics $h$:
- $\forall n \in V ; \forall m \in children(n) ;$
- $h(n) \leq cost(n,m) + h(m)$
無矛盾なhは常に許容的です。証明は以下:
$n_0, n_1, ... n_g=v_g$ として、
- $h(n_0) \leq cost(n_0,n_1) + h(n_1)$
- $h(n_1) \leq cost(n_1,n_2) + h(n_2)$
- ...
- $h(n_{g-1}) \leq cost(n_{g-1},n_g) + h(n_g) = cost(n_{g-1},n_g) + 0$
- $\therefore h(n_0) \leq \sum_{j=0}^{j=g-1} cost(n_j,n_{j+1}) = h^*(n_0)$
無矛盾性の意味するのは、最適経路の上でf値を計算した場合に、f値が単調増加してゆくということです。なぜなら
- $h(n) \leq cost(n,m) + h(m)$
- $g(n)+h(n) \leq g(n)+cost(n,m) + h(m)$
- $g(n)+h(n) \leq g(m) + h(m)$
- $f(n) \leq f(m)$
無矛盾性の意味するもうひとつのことは、このヒューリスティック関数が三角不等式を満たすということです。$h(n)$がゴールまでの距離だったことを思い出してください。これを、距離関数$dist(n_1,n_2)$、つまり引数を2つとる関数で表せば、$h(n)=dist(n,v_g), h(m)=dist(m,v_g)$ ですから、
- $dist(n,v_g) \leq dist(n,m) + dist(m,v_g)$
となります。$cost(n,m)$が$dist(n,m)$である点にも気づけると思います。
近道があるのに教えてくれない
無矛盾でないヒューリスティクスを人間で例えると、言うことがコロコロ変わる信頼の置けない奴という意味です。f値が単調増加しないということは、つまり減る場合があるわけですが、要するに 実は近道があるのに隠して教えてくれない ようなやつです。
無矛盾性は、Aの終了条件に実は大切な意味を持ちます。
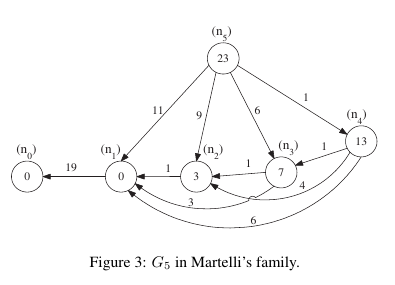
仮に無矛盾でないヒューリスティック $h$ を用いるとします(そういうヒューリスティックはいっぱいあります)。すると、次のように意地悪に設計したグラフでは、最大 $O(2^N)$ 回も、同じノードをreopenする必要が出てきます。(reopen = $g$の値を更新してノードをOPENに再挿入する動作。Dijkstraの記事を参照) ここで、$N$の数はノードの総数、下の図のノードに書いてある数字はhの値、辺に書いてある数字は辺のコストです。(Martelli, 1977)これは、いわばAを騙して騙して騙しまくることに特化したようなシチュエーションだと言えるでしょう。もしも自分の問題のために書いたA*が、許容的にも関わらず異常にに遅い場合は、それがconsistentかどうかを調べてみてください。
(図: Robert C. Holte, Common Misconceptions Concerning Heuristic Search (SoCS 2010) より。)
このお話の続きは、B と PathMaxの時にやります。Bは、このような条件で$O(n^2)$の展開しか行いません。ただし、Bはあまり実用には使われていません。