ダイクストラ探索(1956)

ダイクストラ探索は、エッジのコストが非負のグラフ探索用のアルゴリズムです。均一コスト探索とかいう別名もありますが、ダイクストラというわかりやすい固有名詞で呼ばれることのほうが多いと思います。
(負のコストを含むグラフについてはベルマン・フォード法を使います。
このアドベントでは非負のグラフを中心に紹介をしていきますが、
ベルマンフォードを書いてくれる人がいれば嬉しいです。)

この手法は1956年、奇しくも? ダートマス会議と同じ年に考えられた手法です。
オランダのエドガー・ダイクストラさんに発見されて、本人の名前がついています。
この先生、他にも死ぬほどアルゴリズムを発見されているみたいですね。あんまり知らない。

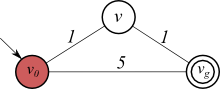
グラフ探索でダイクストラを使う一番の理由は、先ほどの幅優先探索では最適コスト探索を行えないことです。例えば下の図。幅優先では、上のノード $v$ を展開した後、下の辺を通って $v_g$ を展開してしまいます。この時に発見される経路はコスト5です。一方、正しい最適解は、上のノード $v$ を通るコスト2の経路です。

Dijkstra's Algorithm

じゃあ、どーするの? ダイクストラのアルゴリズムは、基本は幅優先探索がベースです。必要な変更点は2つ。

1. キューを 優先度付きキュー にすること。
   2. ノード $n$ の優先度は、スタートからノード$n$までの 現在の 最小コスト。
2. より短い経路が見つかった時に、ノードの最小コストを更新し、キューに再度追加する機能。

これらの変更により、ダイクストラは常に最適解を返すことができます。

最小コストの更新機能が加わったことにより、探索ノードは「まだ調べていないノード」と、「最小コストであることがわかっているノード」に分ける必要があります。この前者を OPEN , 後者を CLOSE と言う集合に保存します。OPENは優先度付きキューですが、CLOSEはただの集合で構いません。実装によっては、CLOSEは明示的なデータ構造が必要ない場合もあります。ダイクストラ始め主要なアルゴリズムの高速な実装を行うための詳細は、Burns et. al. を参照してください。

Burns, Ethan Andrew, et al. "Implementing Fast Heuristic Search Code." Proc. Symposium on Combinatorial Search. 2012.

Algorithm: $Dijkstra(V,E,v_0,v_g)$:

1. Let $OPEN$: a priority queue.
2. Initialize: $push(v_0,cost(v_0),Q)$ 　 /* note: $cost(v_0)=0$ */
3. Until $empty(OPEN)$
   • Let $v \leftarrow popmin(OPEN)$ 　　/* (注1) */
   • $push(v, CLOSE)$ 　　　　　　/* or mark CLOSE */
   • When $v = v_g$ then return $reverse(unfold(parent, v_g))$
   • Else, for each $v' \in children(v)$ do
     • Case $v' \in CLOSE$
       • If $cost(v) + cost(v,v') < cost (v')$
         • $update(v',v)$
         • $remove(v', CLOSE)$
         • $push(v',cost(v'),OPEN)$　　/* reopen node */
     • Case $v' \in OPEN$
       • If $cost(v) + cost(v,v') < cost (v')$
         • $update(v',v)$
         • $remove(v', OPEN)$
         • $push(v',cost(v'),OPEN)$　　/* reinsert node */
     • Otherwise, always
       • $update(v',v)$
       • $push(v',cost(v'),OPEN)$　　/* open node */

• return nil

ただし、 $update(v',v)$ は

• $cost(v')\leftarrow cost(v) + cost(v,v')$
• $parent(v') \leftarrow v$

です。

ノードの新しい最小経路が見つかった場合には、親とコストを更新して再度OPENリストに追加する、というのがアルゴリズムの核です。この場合、下のグラフでは

1. $v_0$を展開(OPENの中の最小コスト0)
2. $v,v_g$ をOPENに追加
3. $v$ を展開(OPENの中の最小コスト1)
4. $v_g$ をReinsert (コスト2)
5. $v_g$ を展開

と動作することで、最適解が求まります。

Dijkstra's Algorithm : Variations

このアルゴリズムにはまだ自由度があります。その1つは、2つ以上のノードが同じ優先度の場合のTiebreaking手法です(注1)。今日は置いときます。

もうひとつの自由度は、OPENの実装にあります。もし辺のコストが整数で、考えられるコストの種類が十分に密なら、 $O(1)$ の配列ベースの実装を用いるのが速いです(配列のインデックスがコスト)。辺のコストが実数値で、沢山のコストが考えられる場合には、ヒープや赤黒木を用いた $O(\log n)$ 挿入 の優先度つきキューが必要です。

以上。