Globally Admissible Heuristics - 大域許容的ヒューリスティクス
この言葉、まだ教科書にも日本語文献にも出てきていないので、訳語は独自です。元々アイディアはあったのですが、今まで述べた内容とは矛盾するようなタイトルの論文、 Karpas, Domshlak, Optimal Search with Inadmissible Heuristics. 2012. ICAPS でまとめられた考え方です。
Globally Admissible heuristics は、 一部の最適解を枝刈りしてしまうが、最低1つの最適解を残す ようなヒューリスティクスです。例えばどんなヒューリスティクスがそれに当てはまるか?
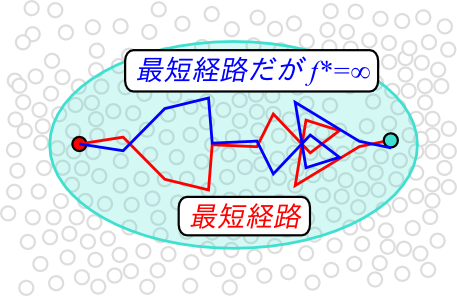
例えば、探索空間の対称性という1つのテーマがあります。このような、スタートとゴールに対して対称な複数の経路のうち、1つの経路を除いて枝刈りする手法のことを、 対称性の破壊 (symmetry breaking) とよびます。
この枝刈りは、一件Aの範疇では捉えられないような気がします。しかし、「特定の条件の時に無限大の値を返すヒューリスティクス」というのを考えれば、このような枝刈りをAの枠組みの中で考えることが出来ます。そのようなヒューリスティクスは、(なにしろ無限大なので) ゴールまでの真の距離h*よりも高い値をノードに割り振る非許容的なヒューリスティクスです。しかし、それが最適解を最低1つ残すのならば、これは大域許容的ヒューリスティクスとして意味のあるヒューリスティクスになります。
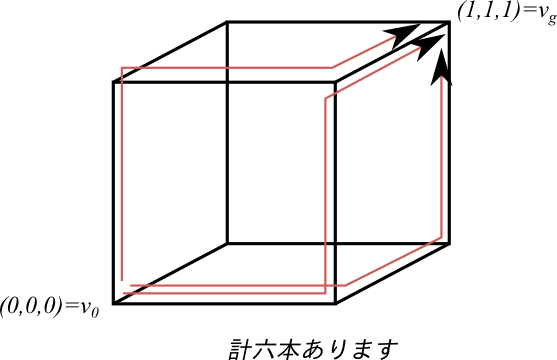
上の図は二次元なので、最大でも1つしか対称性は存在しませんが、高次元空間ではより多くの対称性があります。例えば、(0,0,0)-(1,1,1)の単位立方体の辺上で、(0,0,0)から(1,1,1)への最短経路は6本あります。
こぼれ話。空間の対称性を検知するためには、 グラフ自己同型写像 (Automorphism) のなす群の生成集合 とかいうものを求める必要があるのですが、これは先日準多項式時間で解けることが話題になったグラフ同型問題(GI)より難しいことがわかっている(Luks 1993)ので、対称性検知を伴うヒューリスティクスは、一度計算するたびに難しい問題を解く事になります。PSPACE完全なグラフ問題を解くときには、ループを回すたびにNP完全な問題を解くのは別に普通の選択肢です
また、似ているが似ていない枝刈り手法として、Partial Order Pruningというものがあります。これも、この枠組みでは大域許容的ヒューリスティクスとして考えられます。
ということで、このようなクラスのヒューリスティクスは、非許容的であっても最適解を返せます。二日前の、「ユークリッド距離よりも優れたヒューリスティクス」の例はこれです。下界関数はまだまだ奥が深い!
まとめ
大域許容的ヒューリスティクスの解説を行いました。
次回以降は、同様にヒューリスティクスを用いる探索手法として、Aの変種や、A以外の探索手法を紹介したいと思います。